Algebra Topics -
Negative Numbers

Algebra Topics
Negative Numbers


/en/algebra-topics/exponents/content/
A negative number is any number that is less than zero. For instance, -7 is a number that is seven less than 0.
-7
It might seem a little odd to say that a number is less than 0. After all, we often think of zero as meaning nothing. For instance, if you have 0 pieces of chocolate left in your candy bowl, you have no candy. There's nothing left. It's difficult to imagine having less than nothing in this case.
However, there are instances in real life where you use numbers that are less than zero. For example, have you ever been outside on a really cold winter day when the temperature was below zero? Any temperature below zero is a negative number. For instance, the temperature on this thermometer is -20, or twenty degrees below zero.
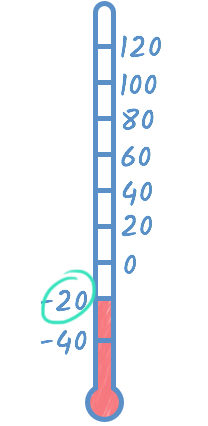
You can also use negative numbers for more abstract ideas. For instance, in finances negative numbers can be used to show debt. If I overdraw my account (take out more money than I actually have), my new bank balance will be a negative number. Not only will I have no money in the bank—I'll actually have less than none because I owe the bank money.
Watch the video below to learn more about negative numbers.
Any number without a minus sign in front of it is considered to be a positive number, meaning a number that's greater than zero. So while -7 is negative seven, 7 is positive seven, or simply seven.
As you might have noticed, you write negative numbers with the same symbol you use in subtraction: the minus sign ( - ). The minus sign doesn't mean you should think of a number like -4 as subtract four. After all, how would you subtract this?
-4
You couldn't—because there's nothing to subtract it from. We can write -4 on its own precisely because it doesn't mean subtract 4. It means the opposite of four.
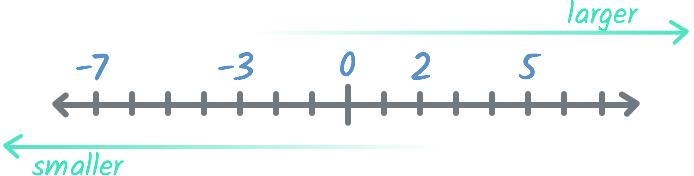
Take a look at 4 and -4 on the number line:

You can think of a number line as having three parts: a positive direction, a negative direction, and zero. Everything to the right of zero is positive and everything to the left of zero is negative. We think of positive and negative numbers as being opposites because they are on opposite sides of the number line.
Another important thing to know about negative numbers is that they get smaller the farther they get from 0. On this number line, the farther left a number is, the smaller it is. So 1 is smaller than 3. -2 is smaller than 1, and -7 is smaller than -2.
When we talk about the absolute value of a number, we are talking about that number's distance from 0 on the number line. Remember how we said 4 and -4 were the same distance from 0? That means 4 and -4 have the same absolute value. We represent taking the absolute value of a number with two straight vertical lines | |. For example, |-3| = 3. This is read "the absolute value of negative three is three."
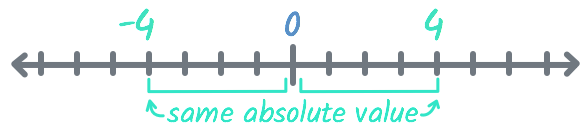
Something important to remember: even though negative numbers get smaller as they get further from 0, their absolute value gets bigger. For example, -10 is smaller than -6. However, |-10| is bigger than |-6| because -10 has a greater distance from 0 than -6.
Using negative numbers in arithmetic is fairly simple. There are just a few special rules to keep in mind.
When you're adding and subtracting negative numbers, it helps to think about a number line, at least at first. Let's take a look at this problem: 6 - 7. Even though 7 is larger than 6, you can subtract it in the exact same way as any other number, as long as you understand there are numbers smaller than 0.

6 - 7 = -1
While the number line makes it easy to picture this problem, there's also a trick you could have used to solve it.
First, ignore the negative signs for a moment. Just find the difference between the two numbers. In this case, it means solving for 7 - 6, which is 1. Next, look at your original problem. Which number has the highest absolute value? In this case, it's -7. Because -7 is a negative number, our answer will be one too: -1. Because the absolute value of -7 is greater than the distance between 6 and 0, our answer ends up being less than 0.
How would you solve this problem?
6 + -7
Believe it or not, this is the exact same problem we just solved!
This is because the plus sign simply lets you know you're combining two numbers. When you combine a negative number with a positive one, the sum will be less than the original number—so you might as well be subtracting. So 6 + -7 is the same thing as 6 - 7, and they both equal -1.
6 + -7 = -1
Whenever you see a positive and negative sign next to each other, you should read it as a negative. Just like 6 + -7 is the same as 6 - 7:
This is true whenever you're adding a negative number. Adding a negative number is always the same as subtracting that number's absolute value.
If adding a negative number is actually equal to subtracting, how do you subtract a negative number? For example, how do you solve this problem?
6 - - 3
If you guessed that you add them, you're right. Here's why: Remember how we said a negative number was the opposite of a positive one? We compared them to you and your mirror image. Your mirror image is your opposite, which means your mirror image's opposite is you. In other words, the opposite of your opposite is you.
In the same way, you can simplify these two minus signs by reading them as two negatives. The first minus sign negates—or makes negative—the second. Because the negative—or opposite—of a negative is a positive, you can replace both minus signs with a plus sign. This means you'd solve for this:
6 + 3
This is a lot easier, to solve, right? If it seems confusing, you can just remember this simple trick: When you see two minus signs back to back, replace them with a plus sign.
So 6 minus negative 3 is equal to 6 plus 3. That's equal to 9. In other words, 6 - -3 is 9.
Remembering all of the rules for adding and subtracting numbers can be overwhelming. Watch the video below for a trick to help you.
There are two rules for multiplying and dividing numbers:


That's it! You multiply or divide as normal, then use these rules to determine whether the answer is positive or negative. For instance, take this problem, -3 ⋅ -4. 3 ⋅ 4 is 12. Because both numbers we multiplied were negative, the answer is positive: 12.
-3 ⋅ -4 = 12
On the other hand, if we were to multiply 3 ⋅ -4, we'd get a different answer:
3 ⋅ -4 = -12
Again, 3 ⋅ 4 is 12. But because one of our multiples is negative and the other is positive, our answer must also be negative: -12.
It works the same way for division. -40 / -10 is 4 because -40 and -10 are both negatives. However, -40 / 10 is -4 because one number is negative and the other is positive.
/en/algebra-topics/reciprocals-and-inverse-numbers/content/