Algebra Topics -
Reading Algebraic Expressions

Algebra Topics
Reading Algebraic Expressions


/en/algebra-topics/reciprocals-and-inverse-numbers/content/
If you're new to algebra—or haven't thought about it in a while—one of the first things you might notice is that algebra problems look a bit different from simple arithmetic problems. Take the expression below, for instance:
x + 4x ⋅ 22 - ( 3 / x )
It's not that difficult to solve once you know how to do it, but it does include a few symbols that are common in algebra but not in more basic math. The way you write algebra expressions is called algebraic notation. While it might look tricky at first, algebraic notation isn't that complicated.
Algebraic notation includes five main components: variables, coefficients, operators, exponents, and parentheses. You can see all five of them in the expression below:
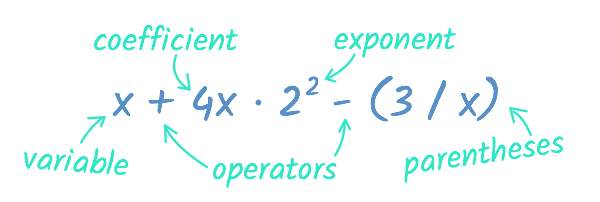
We'll go through these one by one.
A variable is a letter that is used to represent a number. For instance, in this problem the variable x represents an unknown number that will equal 5 when added to 2.
2 + x = 5
In other words, this expression is asking the question, "What number can you add to 2 to get 5?" We wrote x because we didn't know what the number was at first—but we can figure it out. Since we know that 2 + 3 = 5, our variable must be equal to 3. In other words, x = 3.
Although this was a simple addition problem, the fact that it included a variable made it an algebra problem. In fact, finding the value of an unknown number is often the goal in algebra.
While x is the most commonly used variable, any letter can be a variable. An algebra problem can have one variable or many. If a variable is used more than once in the same problem, it's equal to the same number each time. Take this equation:
x + x + y = 20
Each x in this expression is equal to the same amount. The other variable, y, may be equal to a different amount.
Just because you find the value for a variable in one problem doesn't mean the variable will have the same value in a different problem. For instance, while x was equal to 3 in our first problem, it isn't necessarily equal to 3 in any other expression.
Sometimes you'll see a variable with another number in front of it, like this:
2x
In this example, 2 is the coefficient. Coefficients are a way to group variables. For example, 2x is just another way to write x + x. Could you use coefficients to rewrite this expression?
x + x + x + x + y + y + y
Because there are four xs and three ys, you could write this as 4x + 3y. Without knowing what x and y are equal to, we can't simplify it even further—but it is a lot simpler to read:
4x + 3y
You may be wondering why we can't simplify this even further to 7xy. This is because you can only add or subtract variables that are the same—so you can add x + x or y + y but never x + y. For more information about adding and subtracting variables, check out our Simplifying Expressions lesson.
Operators are the symbols that tell us what to do in math problems. You've seen them all before:
+ - ÷ x
These symbols let you know how to calculate an expression—for instance, when you see the plus sign you know to add two numbers, and when you see the minus sign you know to subtract. The plus and minus signs are the same in algebra, but multiplication and division might be written a bit differently.
In arithmetic, multiplication is usually written as like this:
2 x 6
However, in algebra the multiplication symbol is written a bit differently. This is because x looks similar to the variable x. For this reason, many people use this dot symbol to show multiplication: ⋅ (which is what you'll see in our lessons). In algebra, a multiplication problem is written like this:
2 ⋅ 6
There are a few other ways to show multiplication in algebra. As you saw when we multiplied coefficients, you can simply write variables next to each other to multiply them. If you wanted to multiply x and y, you could simply write xy.
xy
There are a few ways to show division in algebra. You're probably most familiar with division problems that look like this:
4 ÷ 2
You will see division written this way in algebra. However, you'll also see it written like this (especially in our lessons):
4 / 2
If you're dividing groups of numbers, you can also show division with a horizontal line. For example, look at this problem:
| 3x - 12y + 18 |
| 3 |
Here, everything above the line is divided by everything below it, so you'd divide 3x - 12y + 18 by 3.
You're probably used to seeing parentheses used in writing, most often with part of a sentence that isn't essential (although they can also be used for other things). In algebra, parentheses are used a bit differently. Parentheses are used to group parts of an algebraic expression. When you see part of an algebra problem enclosed in parentheses, you'll need to solve that part before tackling the rest of the problem.
7 + (40 / x) = 15
In this problem, you would start by solving everything in the parentheses first; then you'd solve everything else.
Curious about why you solve the part in parentheses first? Check out our lesson on the order of operations.
What happens when two sets of parentheses are next to each other, without any operators in between?
(3)(5)
If you remembered that two variables next to each other are multiplied, you might guess that you would multiply two sets of parentheses side by side too. So (3)(5) is equal to 3 ⋅ 5, which is equal to 15.
Exponents are numbers that have been multiplied by themselves. For instance, let's look at the exponent 103.
103
103 is simply another way of saying 10 has been multiplied by itself 3 times. In other words, it's equal to 10 ⋅ 10 ⋅ 10. You can learn more in our exponents lesson.
/en/algebra-topics/writing-algebraic-expressions/content/