Algebra Topics -
Reciprocals and Inverse Numbers

Algebra Topics
Reciprocals and Inverse Numbers


/en/algebra-topics/negative-numbers/content/
Every number has an opposite. In fact, every number has two opposites: the additive inverse and the reciprocal—or multiplicative inverse. Don't be intimidated by these technical-sounding names, though. Finding a number's opposites is actually pretty straightforward.
The first type of opposite is the one you might be most familiar with: positive numbers and negative numbers. For example, the opposite of 4 is -4, or negative four. On a number line, 4 and -4 are both the same distance from 0, but they're on opposite sides.
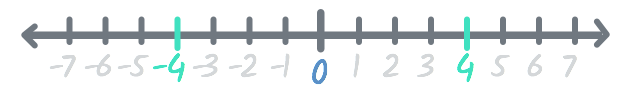
This type of opposite is also called the additive inverse. Inverse is just another word for opposite, and additive refers to the fact that when you add these opposite numbers together, they always equal 0.
-4 + 4 = 0
In this case, -4 + 4 equals 0. So does -20 + 20 and -x + x. In fact, any number you can come up with has an additive inverse. No matter how large or small a number is, adding it and its inverse will equal 0 every time.
If you've never worked with positive and negative numbers, you might want to review our lesson on negative numbers.
| x | → | -x |
| 3y | → | -3y |
| -y | → | y |
| -6x | → | 6x |
The main time you'll use the additive inverse in algebra is when you cancel out numbers in an expression. (If you're not familiar with cancelling out, check out our lesson on simplifying expressions.) When you cancel out a number, you're eliminating it from one side of an equation by performing an inverse action on that number on both sides of the equation. In this expression, we're cancelling out -8 by adding its opposite: 8.
| x | - 8 | = | 12 |
| + 8 | + 8 |
Using the additive inverse works for cancelling out because a number added to its inverse always equals 0.
The second type of opposite number has to do with multiplication and division. It's called the multiplicative inverse, but it's more commonly called a reciprocal.
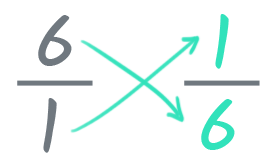
To understand the reciprocal, you must first understand that every whole number can be written as a fraction equal to that number divided by 1. For example, 6 can also be written as 6/1.
| 6 | = | 6 |
| 1 |
Variables can be written this way too. For instance, x = x/1.
| x | = | x |
| 1 |
The reciprocal of a number is this fraction flipped upside down. In other words, the reciprocal has the original fraction's bottom number—or denominator—on top and the top number—or numerator—on the bottom. So the reciprocal of 6 is 1/6 because 6 = 6/1 and 1/6 is the inverse of 6/1.
Below, you can see more reciprocals. Notice that the reciprocal of a number that's already a fraction is just a flipped fraction.
| 5y | → | 1 |
| 5y |
| 18 | → | 1 |
| 18 |
| 3 | → | 4 |
| 4 | 3 |
And because reciprocal means opposite, the reciprocal of a reciprocal fraction is a whole number.
| 1 | → | 7 |
| 7 |
| 1 | → | 2 |
| 2 |
| 1 | → | 25 |
| 25 |
From looking at these tables, you might have already noticed a simpler way to determine the reciprocal of a whole number: Just write a fraction with 1 on top and the original number on the bottom.
Decimal numbers have reciprocals too! To find the reciprocal of a decimal number, change it to a fraction, then flip the fraction. Not sure how to convert a decimal number to a fraction? Check out our lesson on converting percentages, decimals, and fractions.
If you've ever multiplied and divided fractions, the reciprocal might seem familiar to you. (If not, you can always check out our lesson on multiplying and dividing fractions.) When you multiply two fractions, you multiply straight across. The numerators get multiplied, and the denominators get multiplied.
| 4 | ⋅ | 2 | = | 8 |
| 5 | 3 | 15 |
However, when you divide by a fraction you flip the fraction over so the numerator is on the bottom and the denominator is on top. In other words, you use the reciprocal. You use the opposite number because multiplication and division are also opposites.
| 4 | ÷ | 2 | = | 4 | ⋅ | 3 | = | 12 | ||||
| 5 | 3 | 5 | 2 | 10 |
Use the skills you just learned to solve these problems. After you've solved both sets of problems, you can scroll down to view the answers.
Find the additive inverse:
Find the reciprocal:
/en/algebra-topics/reading-algebraic-expressions/content/