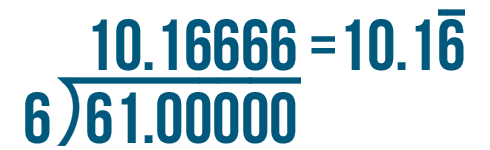/en/multiplicationdivision/introduction-to-division/content/
Long division
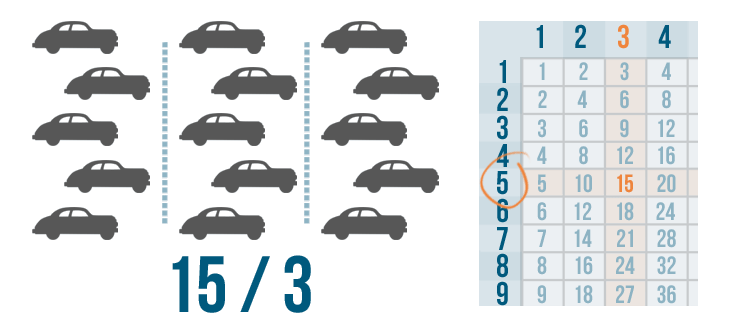
When you divide a number, you are splitting it equally. In Introduction to Division, you learned that division can be a way to understand real-life situations. For example, imagine a car dealership has 15 cars. The manager wants the cars parked in three equal rows.
You could write the situation like this and use a times table to solve it:
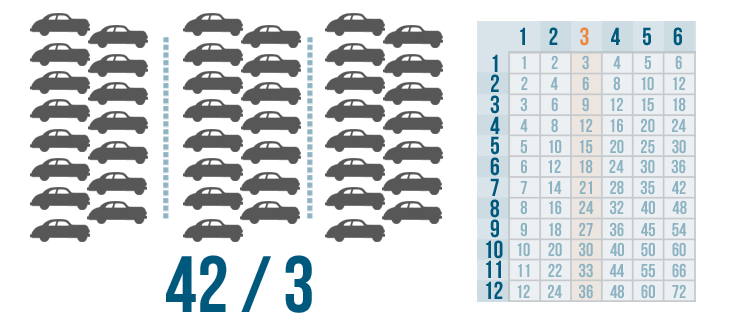
After the cars are divided, counting them shows that each row should have five cars. Now, let's say the car dealership has 42 cars and the manager wants to park them in three rows. The situation would look like this:
This problem is harder to solve. It would take a lot of time to divide that many cars into three groups. Plus, there's no 42 in the 3's column on the times table. Fortunately, there is a way to set up the problem that makes it easy to solve one step at a time. It's called long division.
Let's learn how to set up these problems. We'll look at the problem we discussed above: 42 / 3.

In the last lesson, we learned how to write division expressions.

However, dividing a larger number is easier when the expression is written in a different way.

Instead of writing the numbers side by side with a division symbol...

Instead of writing the numbers side by side with a division symbol... we'll use a different symbol called a division bracket.
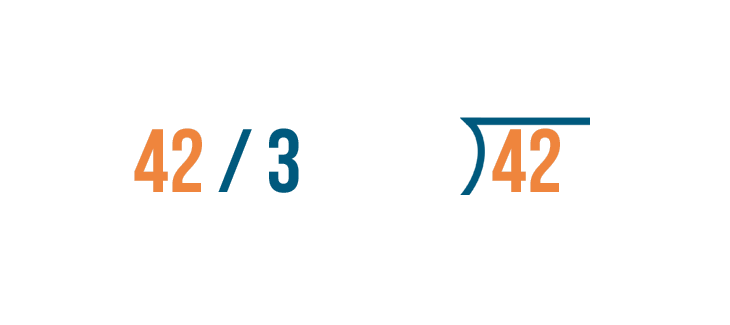
The number you're dividing goes under the division bracket. That's 42.
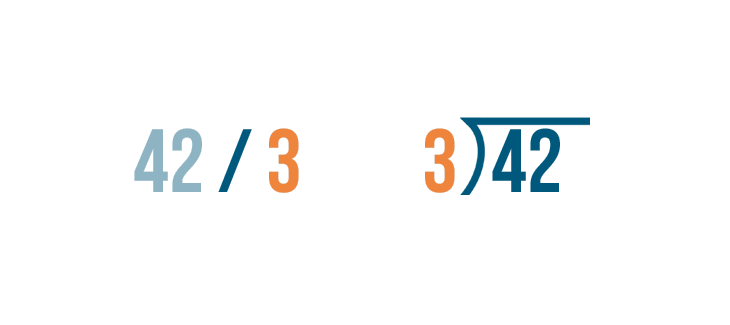
To the left of the division bracket, write the number you're dividing by. In our problem, it's 3.
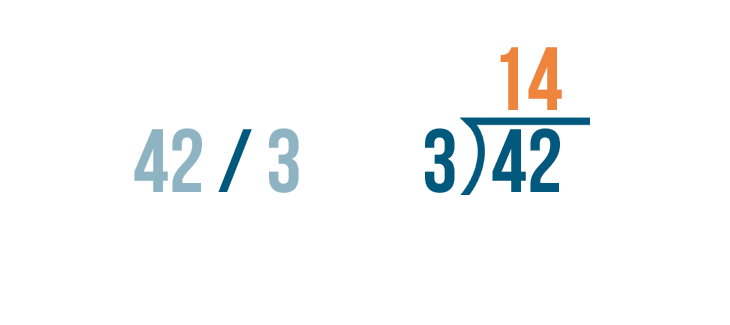
The division bracket is also an equals sign. The quotient, or answer, is written above it.

Let's try setting up another expression, 125 / 5. First, write the division bracket.

Next, write the number being divided, 125.

Finally, write the number we're dividing by, 5.

Remember, you should be careful to set up long division problems correctly.

The number you're dividing goes under the division bracket...

The number you're dividing goes under the division bracket... and the number you're dividing by goes to the left of it.
Solving long-division problems
To solve long division problems, you'll use three math skills you've already learned: division, multiplication, and subtraction. It's a good idea to make sure you feel comfortable with all three skills. If you think you might need more practice, take some time to review those lessons first.
When solving a long division problem, the number under the division bracket is split into smaller numbers. This makes division easier. Plus, you can use a familiar tool, like a times table, to help.
Let's see how solving a long division problem works.
Remember the manager of the used car dealership who wanted to divide 42 cars among 3 rows? Let's find out how many cars he should put in each row.

We'll use long division to solve this problem: 42 / 3.

Long division follows a pattern. You follow the same basic steps again and again until the problem is complete. If this seems confusing, don't worry. We'll go through it step by step.
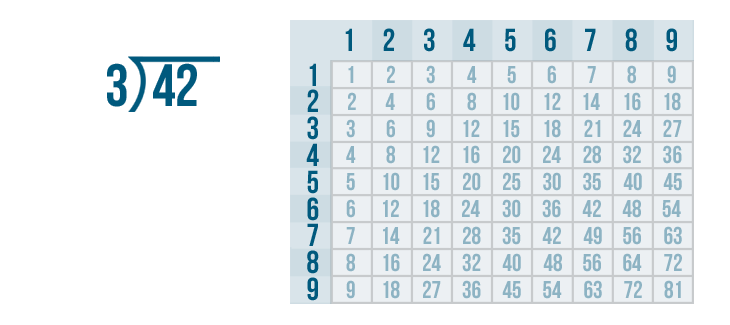
We'll begin with the left digit under the division bracket. That means we'll start with the 4...
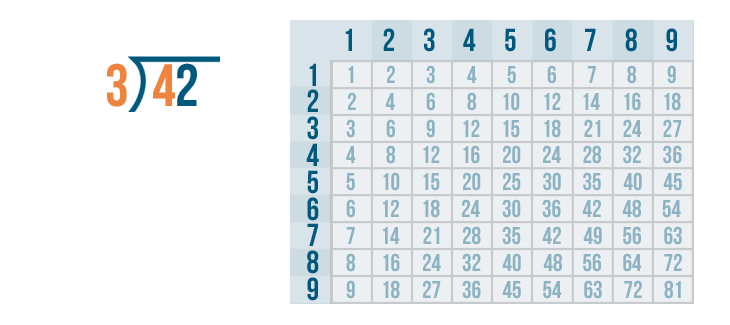
We'll begin with the left digit under the division bracket. That means we'll start with the 4... and we'll figure out how many times it can be divided by 3.

Now it's time to solve 4 / 3.
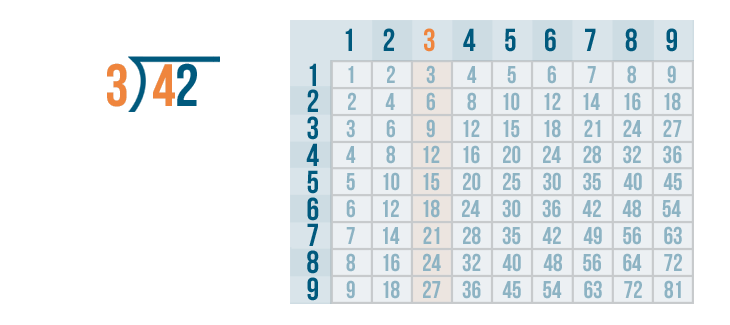
We can use the times table. We'll look at the 3's column.

Since 4 is the number we're dividing, we need to locate the number that is the closest to 4. The number can't be any larger than 4.
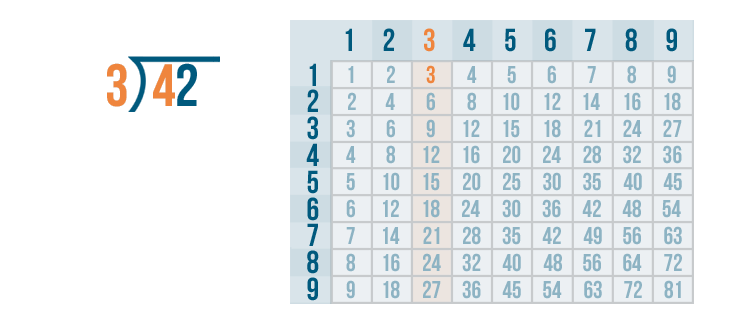
3 is the closest to 4.
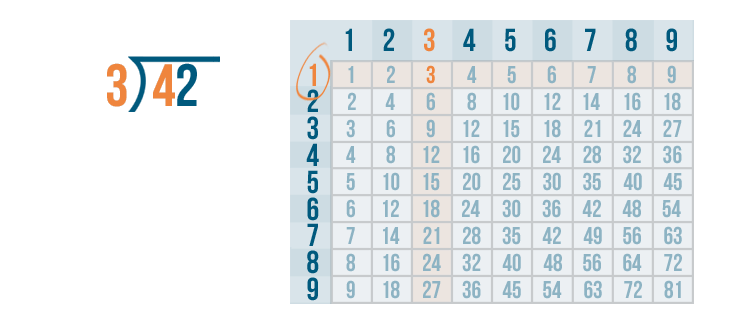
Next, we'll find the row 3 is located in. It's the 1's row.

That means 3 goes into 4 one time.
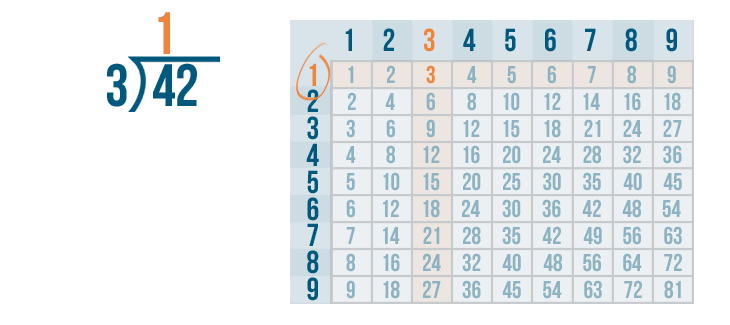
We'll write 1 above the 4 and the division bracket.
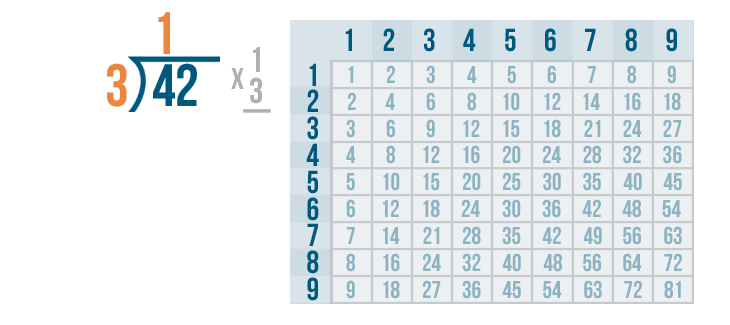
The next step is to multiply the 1 and 3.
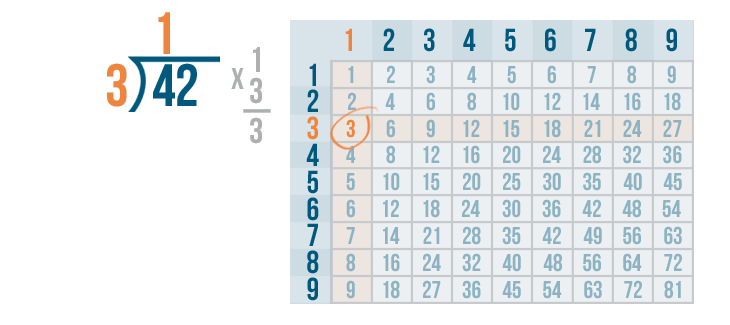
Whenever you multiply a number by 1, that number stays the same. So 1 x 3 is 3.
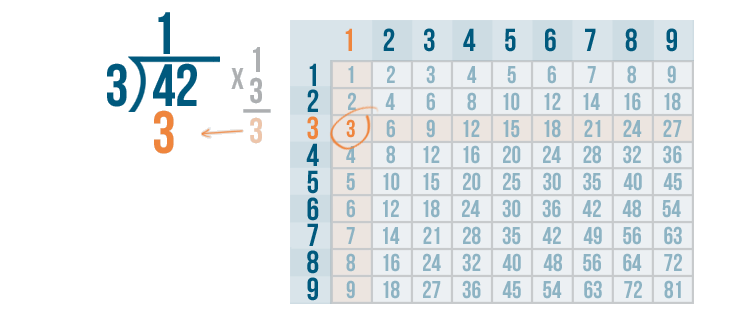
We'll write 3 below the 4.
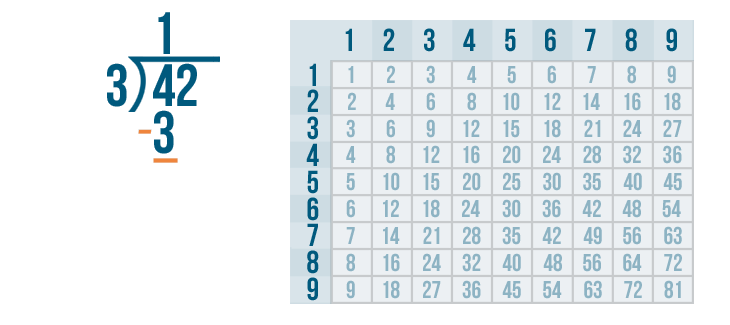
The next step is to subtract.
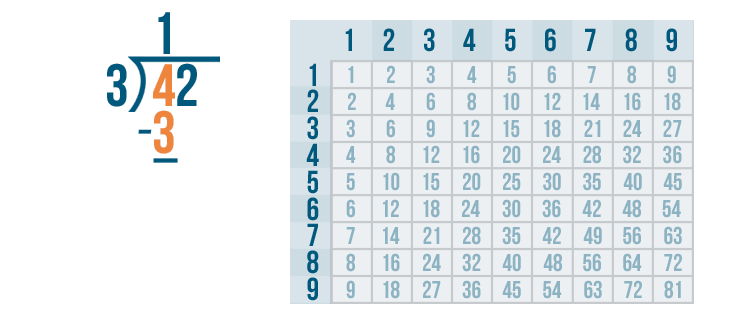
Now we solve 4 - 3.
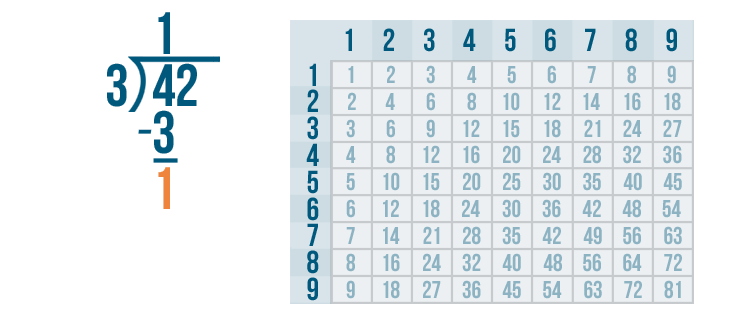
4 - 3 is 1. We'll write 1 below the 4 and 3.
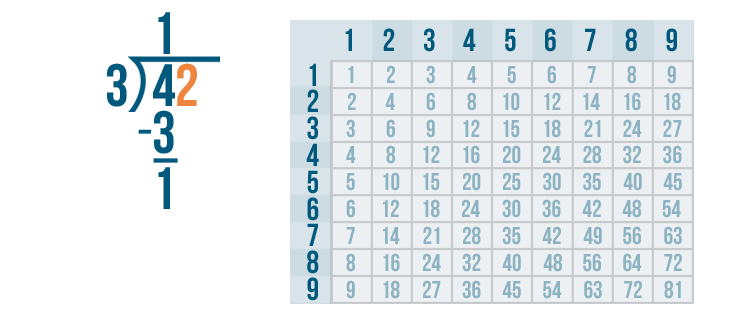
Since our answer is 1, we're not done yet. We'll know our problem is complete when the answer to our subtraction problem is zero. Plus, there's still another digit under the bracket: 2.
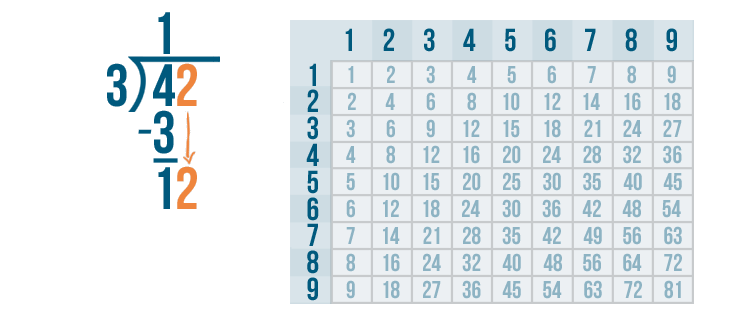
We'll bring the 2 down and rewrite it next to the 1.
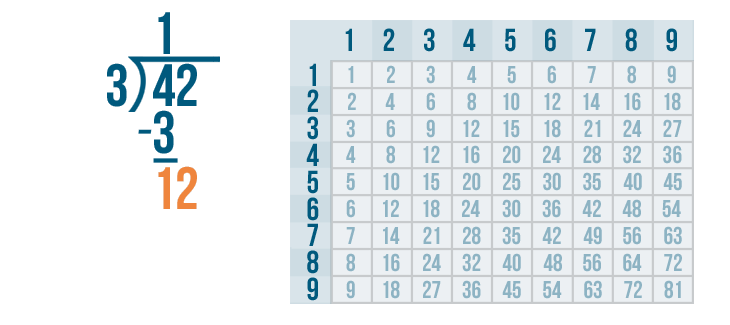
See how the 1 and 2 look like the number 12? That's the next number we need to divide.
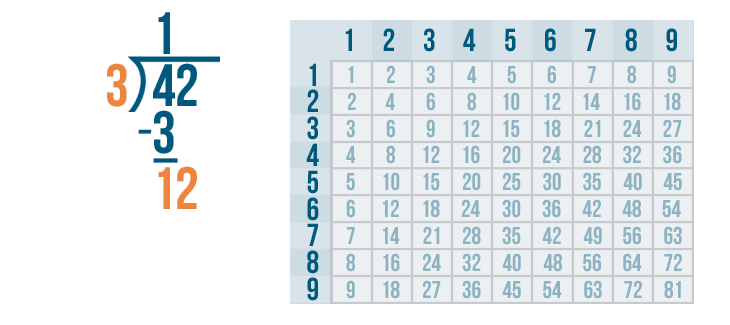
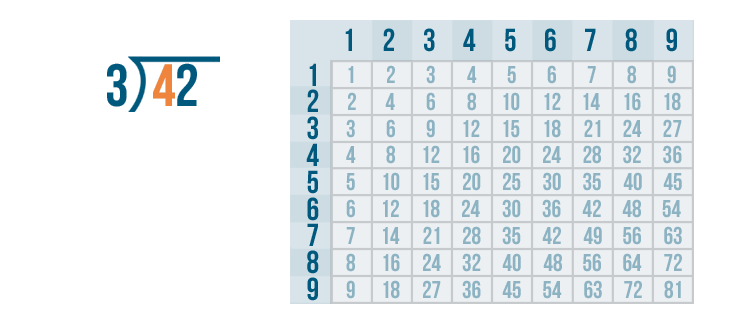
12 is large enough to be divided, so we'll figure out how many times it can be divided by 3.
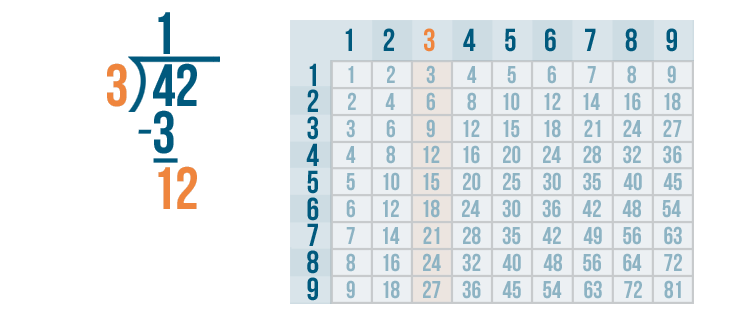
Let's look at the 3's column. Since 12 is the number we're dividing, we'll find the number closest to 12. Remember, the number can't be any larger than 12.
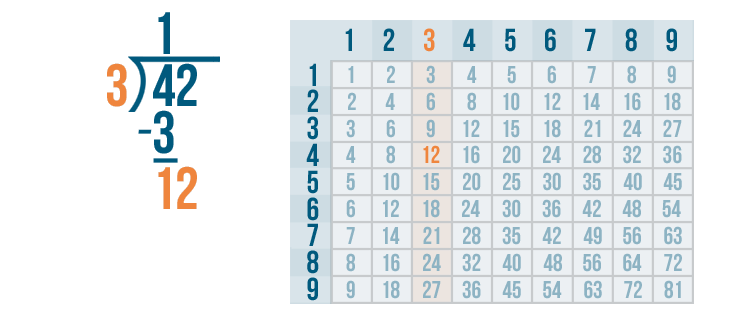
The 3's column has a 12. It would be impossible to get closer than that!

Now we find the row 12 is located in.
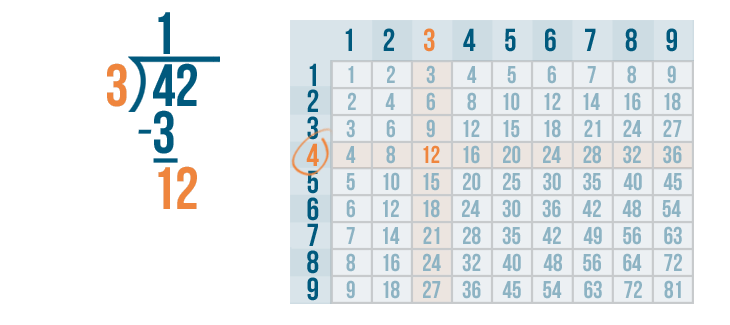
It's the 4's row. 3 goes into 12 four times.
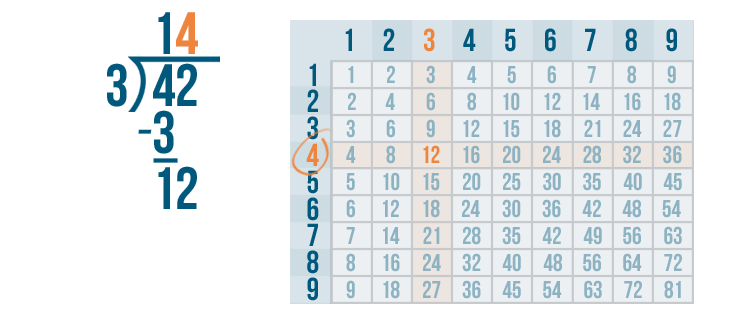
We'll write 4 above the 2 and the division bracket.
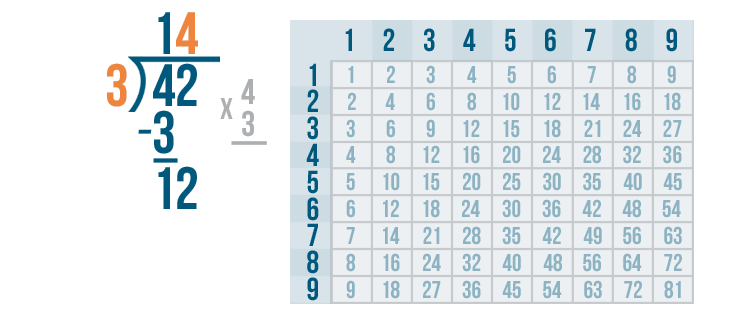
Now it's time to multiply the 4 and 3.
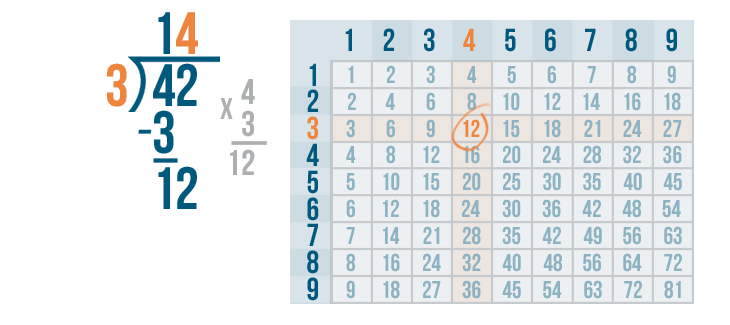
4 x 3 is 12.
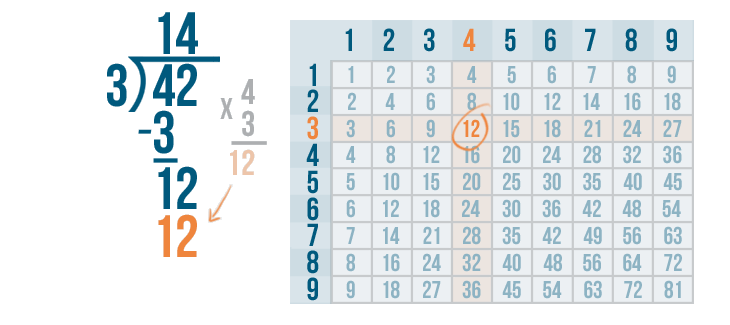
Write the 12 beneath the 12.
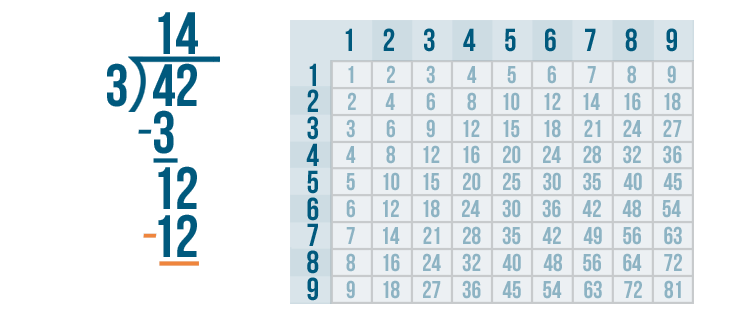
We'll set up our subtraction problem.
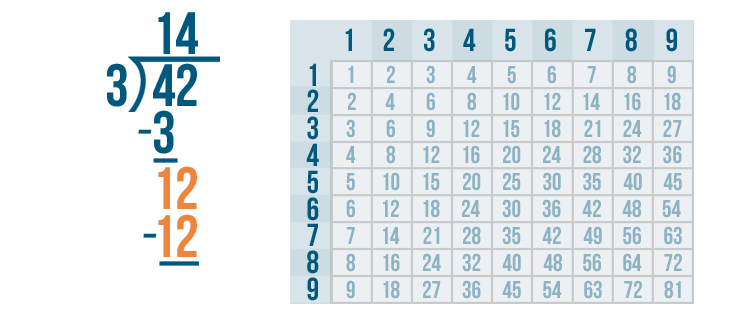
Now it's time to solve 12 - 12.
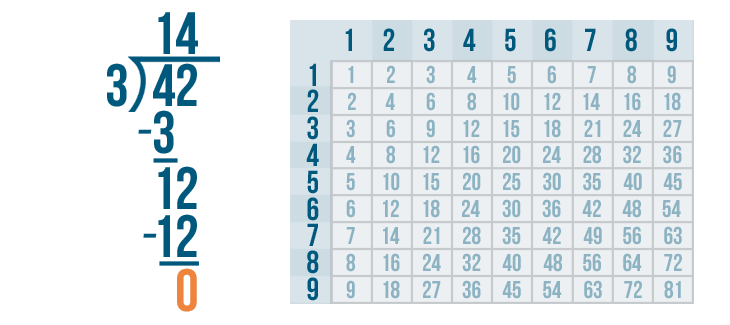
12 - 12 is 0. Write 0 beneath the line directly below the 2 and 2.
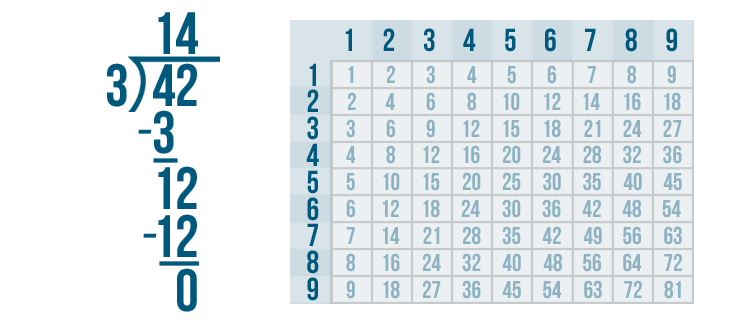
The answer to our subtraction problem is 0. That means we're done! 42 / 3 = 14.

Try this!
Solve these long division problems. Then, check your answer by typing it in the box.
Problems with remainders
In Introduction to Division, you learned that some numbers can't be equally divided. When that happens, there will be an amount left over. This is called a remainder. For instance, let's say you want to share 8 treats equally among your 3 dogs. The answer is that each dog would get two treats with a remainder of two.
The remainder is written as part of the quotient: 8 / 3 = 2 r2.
Long division problems can have remainders too. Watch the slideshow to see how.
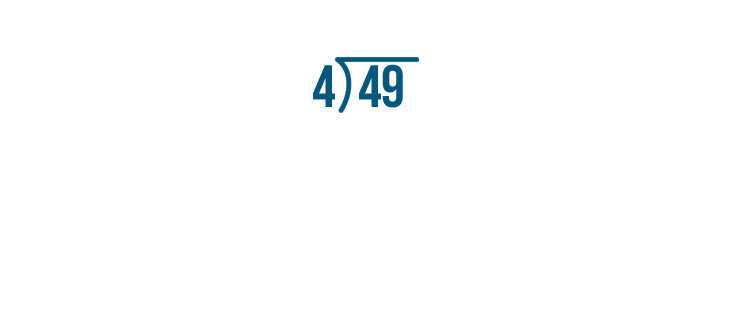
Let's try this problem, 49 / 4.
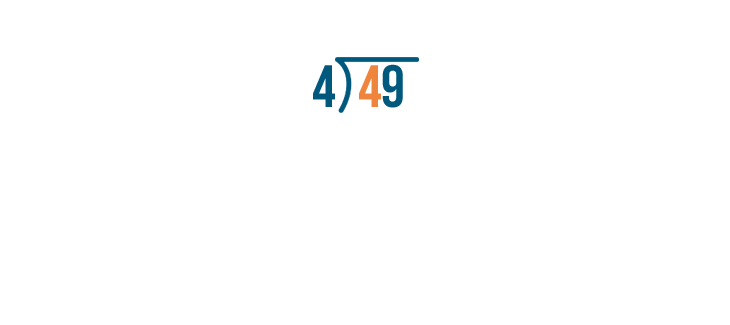
As always, start by dividing the left digit. This means we'll solve for 4 / 4.
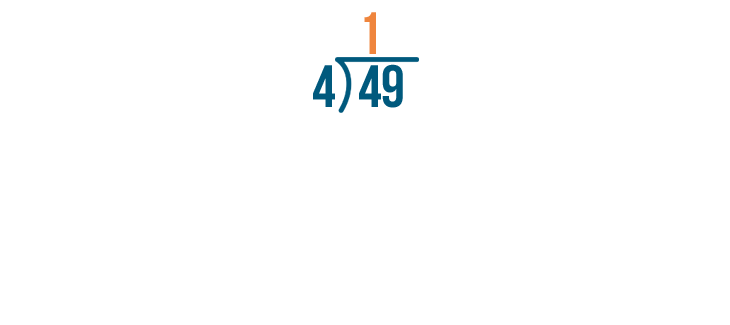
4 / 4 is 1.
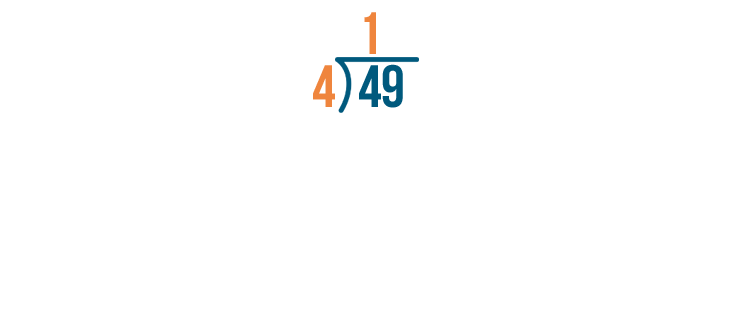
Next, we'll multiply the answer we just got, 1, by the number we're dividing by, 4. So 4 x 1.
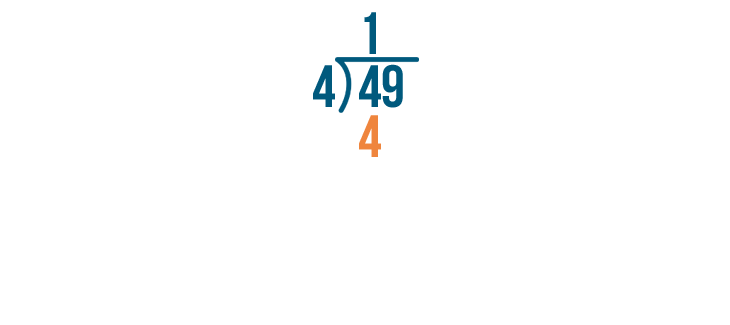
4 x 1 is 4.
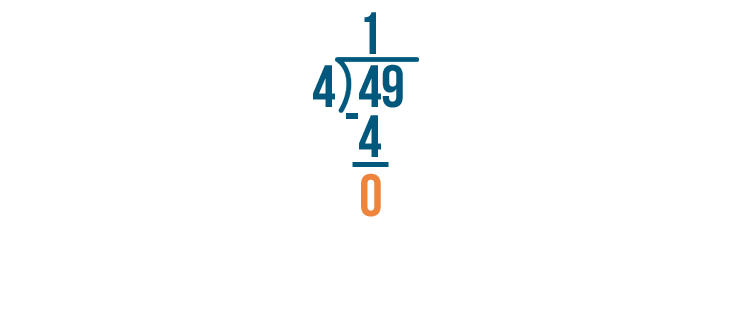
Next, subtract 4 - 4. Whenever you subtract a number from the same number, the answer is 0. So 4 - 4 = 0.
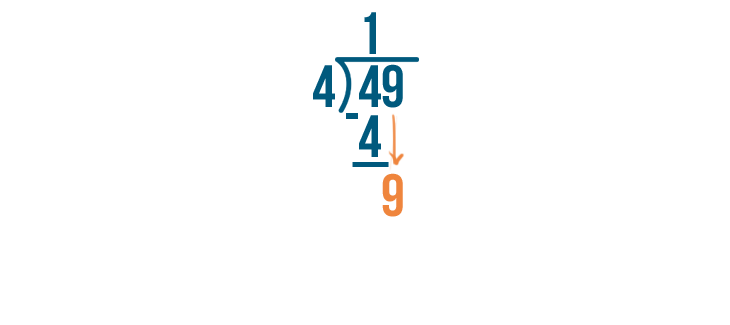
Our problem's not done. The next digit in the number we're dividing is 9. We'll solve for 9 / 4.
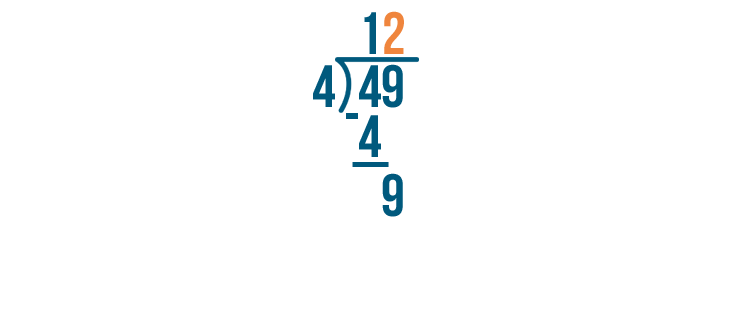
9 / 4 is 2.
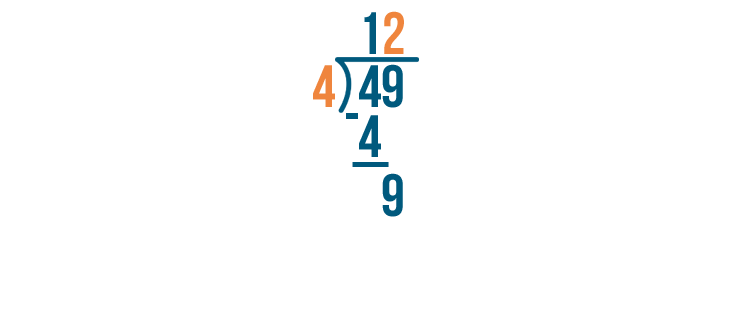
Again, we'll multiply the number we just wrote by the number we're dividing by.
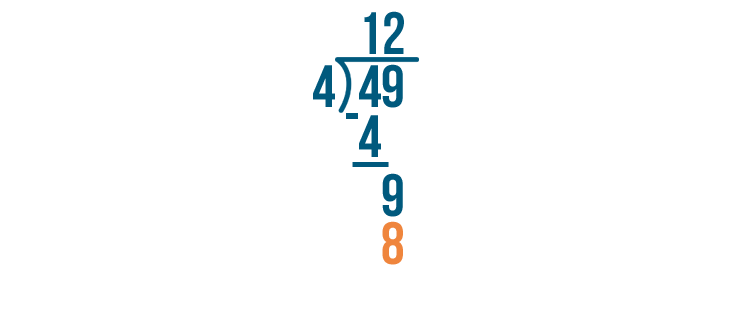
2 x 4 is 8.
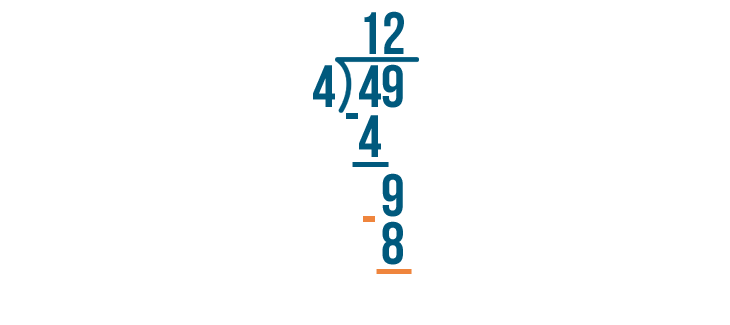
We'll subtract that number, 8, from the number we were dividing.
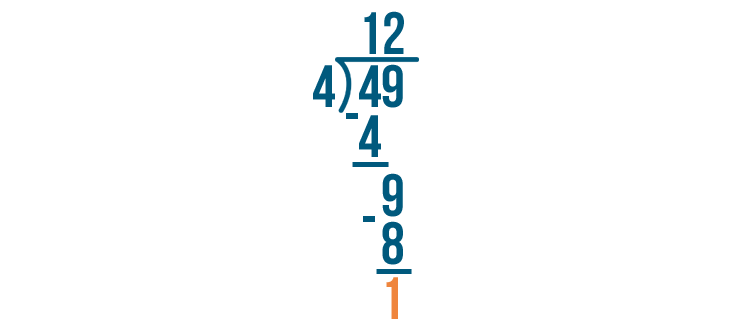
9 - 8 is 1.
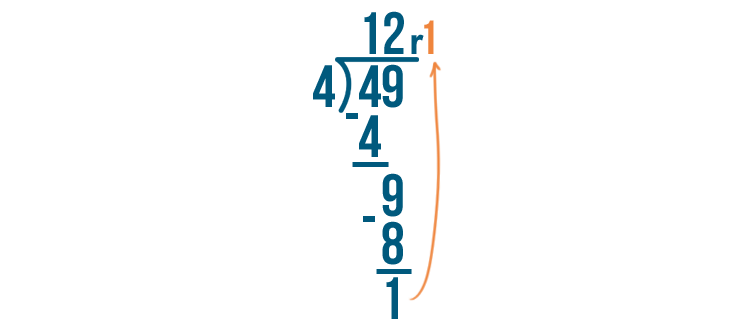
Since 1 is smaller than 4, we can't divide it any further. 1 is our remainder. We'll write it next to the rest of the answer.
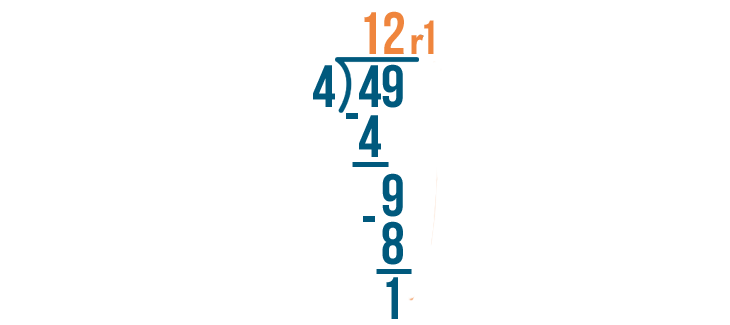
We're done! 49 / 4 = 12, with a remainder of 1.
Try this!
Solve these division problems with remainders. Then, check your answer by typing it into the boxes.
Decimal quotients
On the last page, you learned how to find the remainder for a long division problem that can't be solved evenly. Remainders can be useful if you need to know how much is left over when you divide something, but they might not be very useful in every situation. For example, what if you wanted to divide a 9-foot-long board into 4 equal pieces? That problem could look like this:
9 / 4 = 2 r1
In other words, when you divide a board that's nine feet long into four pieces, each piece will be two feet long. There will be one foot left over.
What if you don't want to waste any wood? In that case, you can continue to divide until there is no longer a remainder. That way, you'd have four equal pieces of wood, with none left over. That problem would look like this:
9 / 4 = 2.25
The answer, 2.25, is a decimal number. You can tell, because it includes a symbol called a decimal point (.). The number to the left of the decimal point, 2, is the whole number. The rest of the answer, .25, shows the part of the number that didn't divide evenly.
Click through the slideshow below to learn how to find the decimal answer to a division problem.
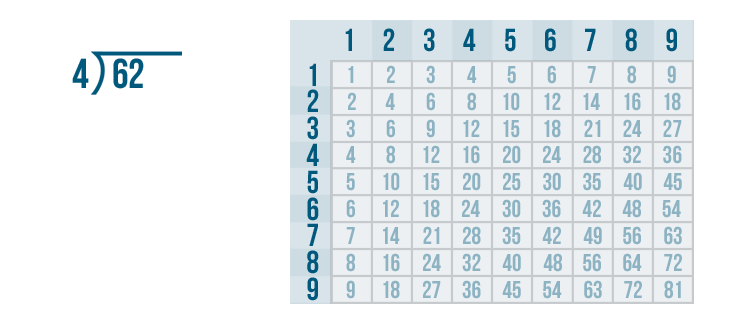
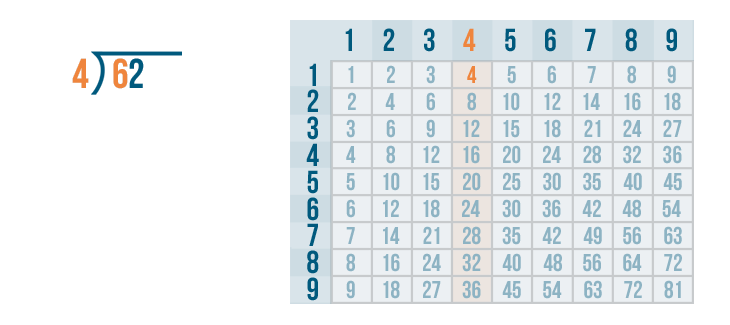
Let's say we have 62 treats to divide equally among 4 dogs. The problem we're solving is 62 / 4. Let's find out how many treats each dog should get.
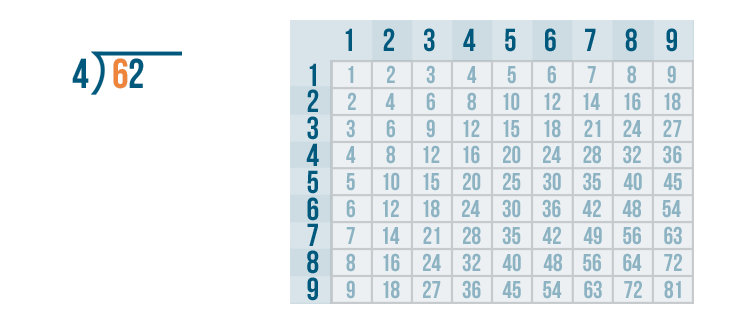
As always, we'll begin with the left digit under the division bracket. That means we'll start with the 6...
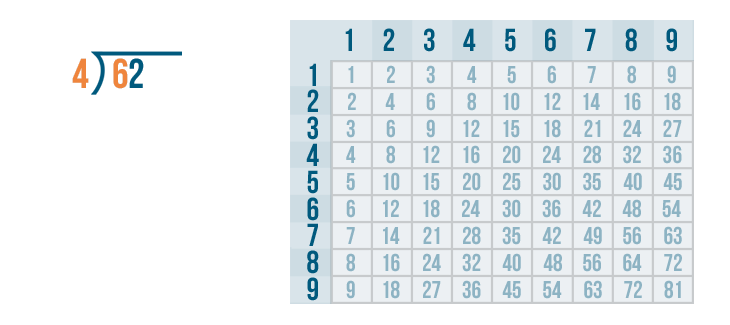
As always, we'll begin with the left digit under the division bracket. That means we'll start with the 6... and we'll figure out how many times it can be divided by 4.

Now it's time to solve 6 / 4. We'll use the times table.
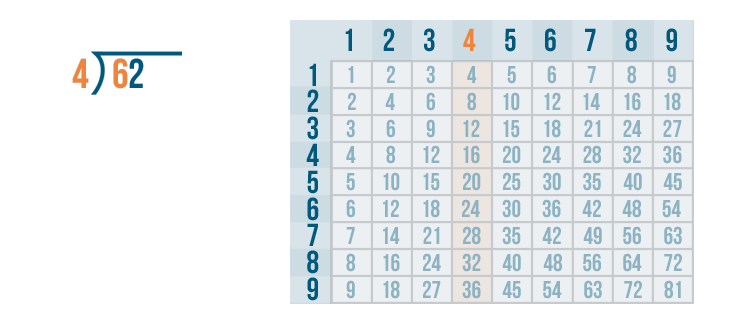
We'll look at the 4's column. Since 6 is the number we are dividing, we need to find the number that is closest to 6. Remember, it can't be any larger than 6.
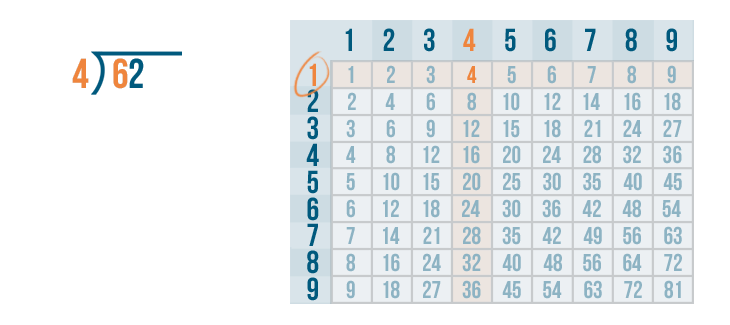
4 is the closest to 6.
Next, we'll find the row 4 is located in. It's the 1's row.
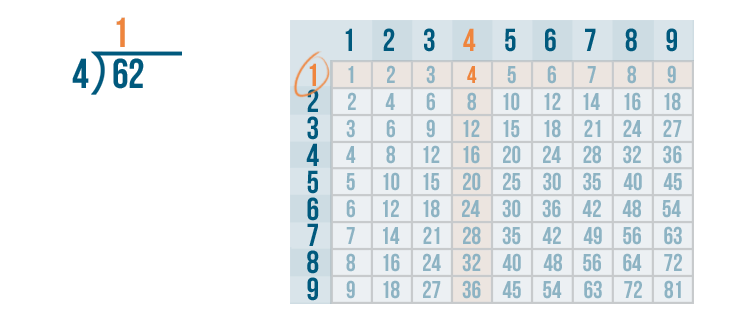
That means 4 goes into 6 one time. We'll write 1 above the 6.
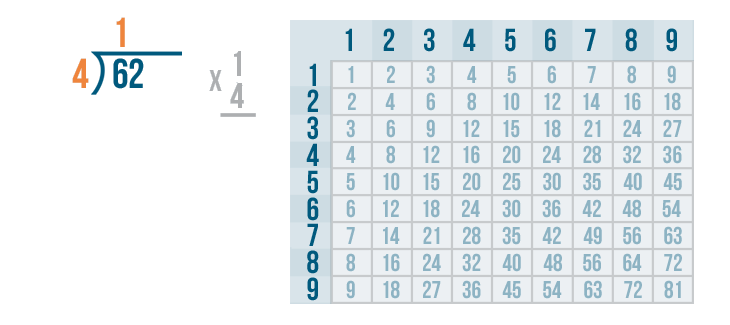
Next, we'll multiply the 1 and 4.
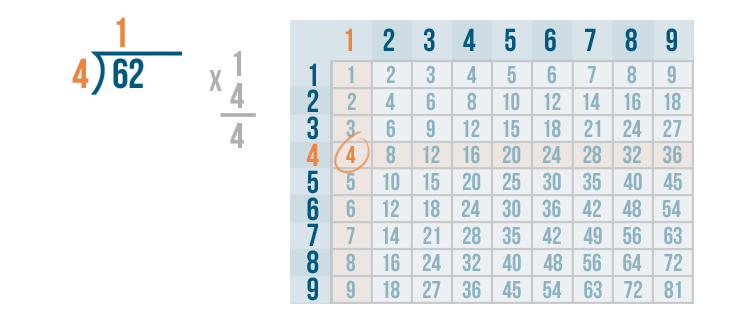
Remember, whenever you multiply a number by 1, that number always stays the same. So 1 x 4 is 4.
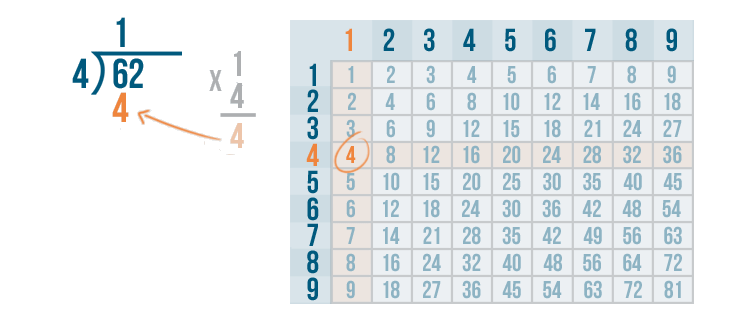
We'll write 4 below the 6.
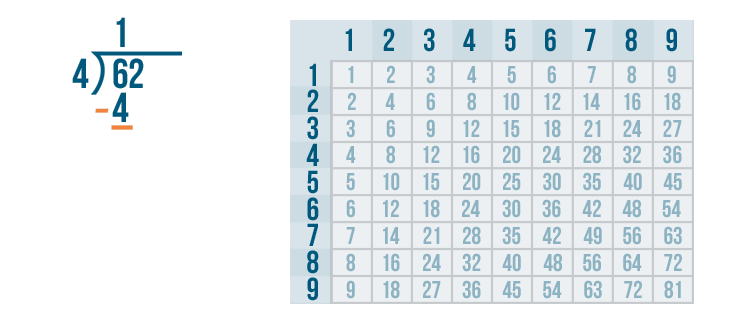
The next step is to subtract.
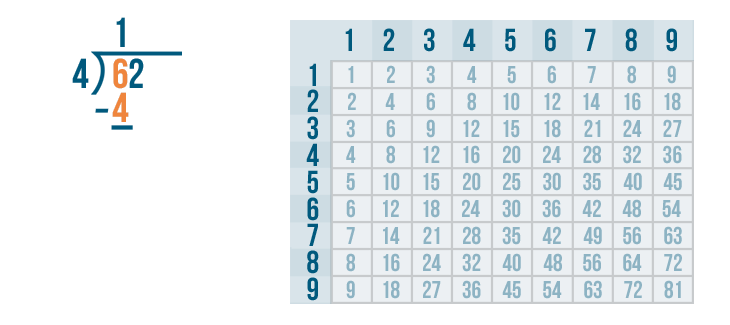
Now we solve 6 - 4.
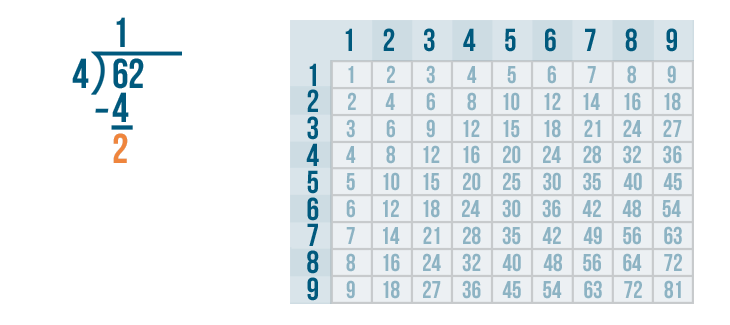
6 - 4 is 2. We'll write 2 below the line.

Since 2 is more than zero, we know we're not done with our problem.
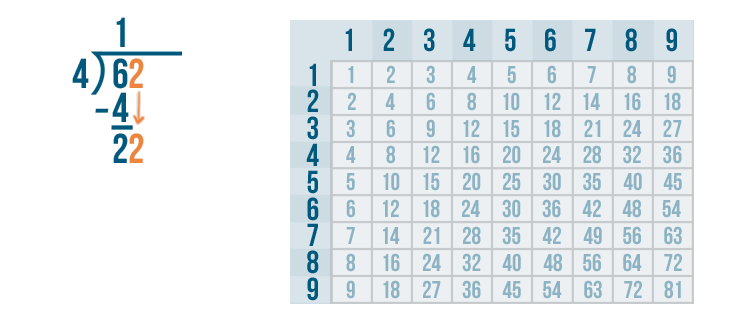
We'll bring the 2 down and rewrite it next to the 2.
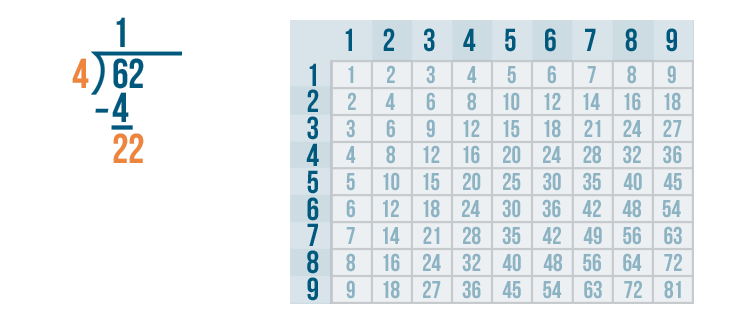
22 is large enough to be divided, so we'll figure out how many times it can be divided by 4.
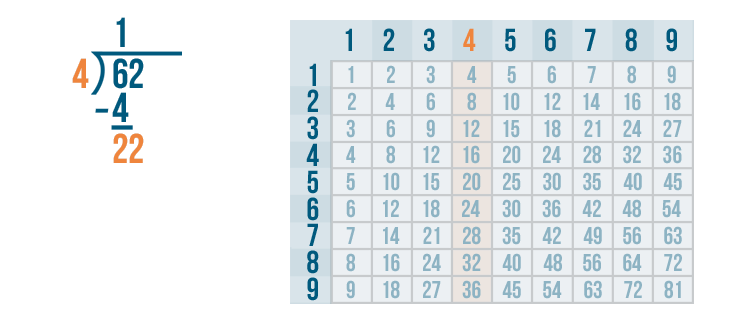
Let's look at the 4's column to locate the number closest to 22. The number can't be any larger than 22.
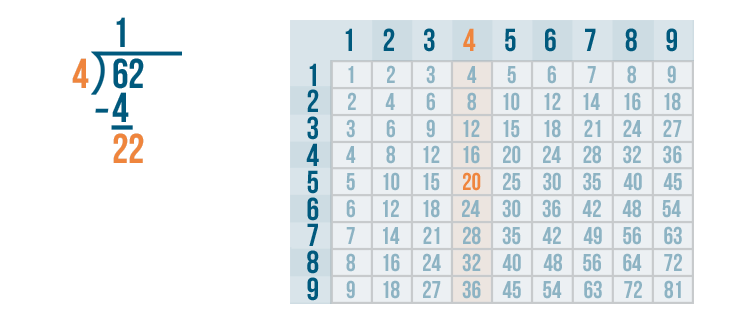
20 is the closest to 22.
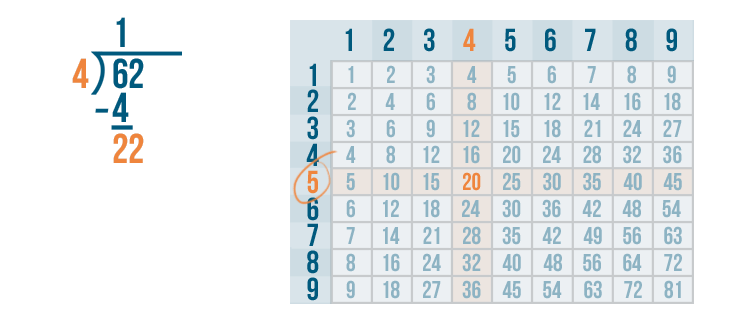
Now we'll find the row 20 is located in. It's the 5's row. So 4 goes into 20 five times.
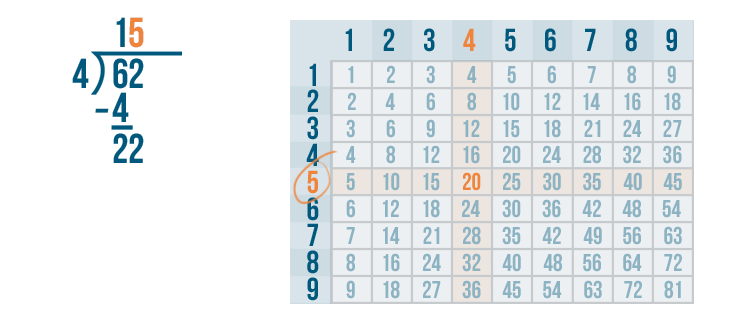
We'll write 5 above the 2.
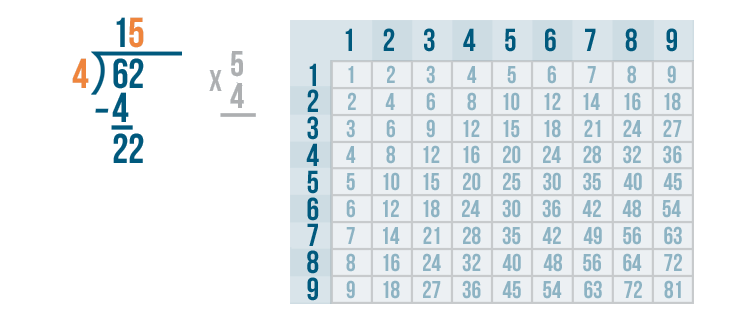
Now we need to multiply the 5 and 4.
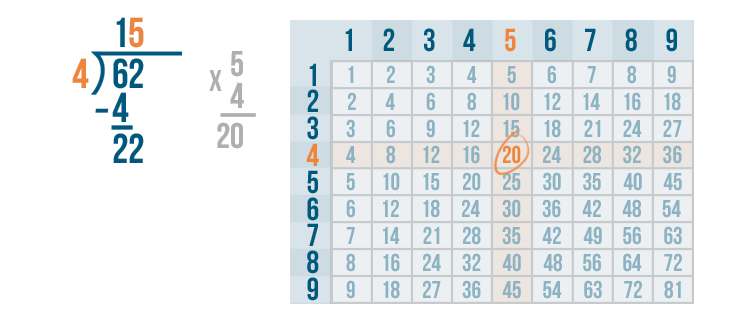
5 x 4 is 20.
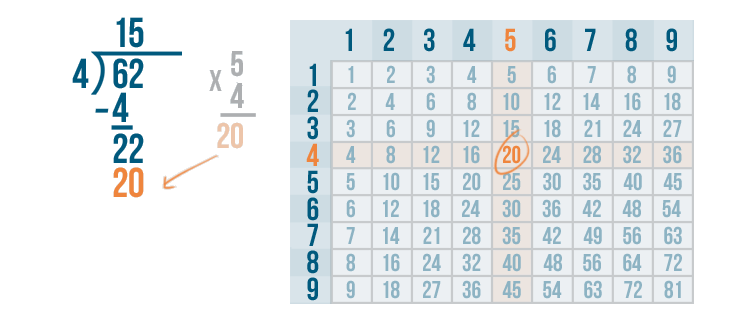
We'll write 20 beneath the 22.
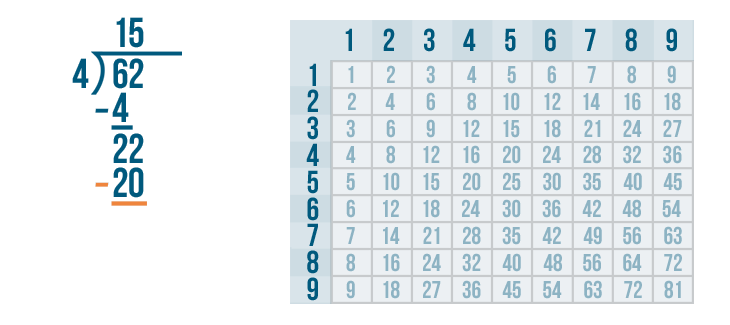
We'll set up our subtraction problem.
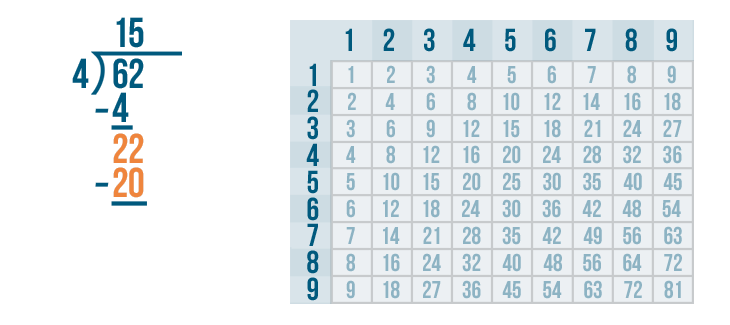
Now it's time to solve 22 - 20.
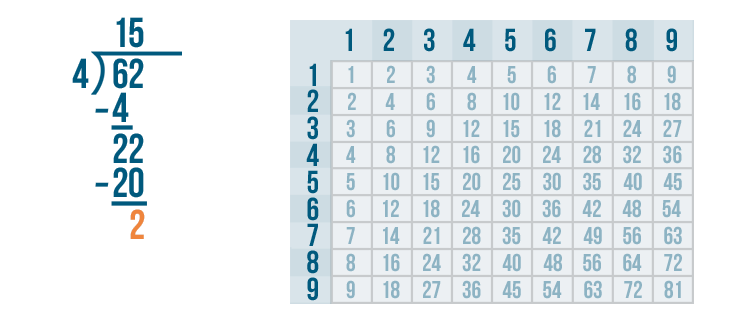
22 - 20 is 2. We'll write 2 beneath the line directly below the 2 and 0.

The answer to the last subtraction problem is more than zero, so we'll look under the bracket to see if there is another digit we can bring down.
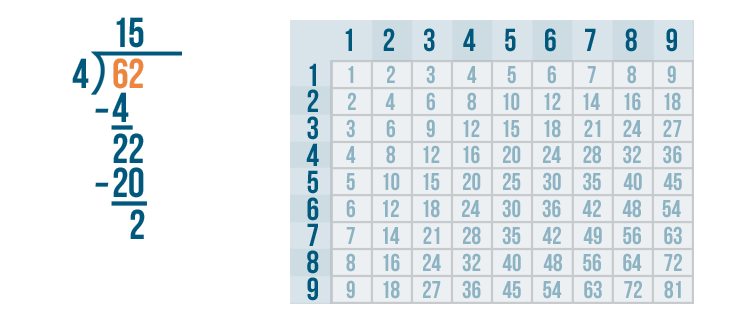
We've divided both of those digits. That means there are no more digits to bring down. But if we write another digit next to 62, we could bring that digit down.

We don't want to make the 62 any larger. That would change our problem. We only had 62 bones to divide.
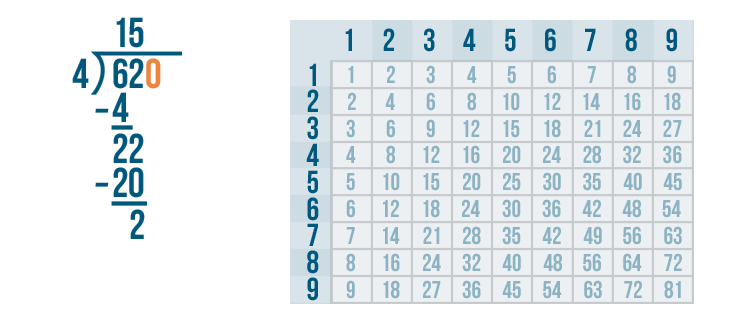
So next to the 62, we'll write the number that means nothing: 0.
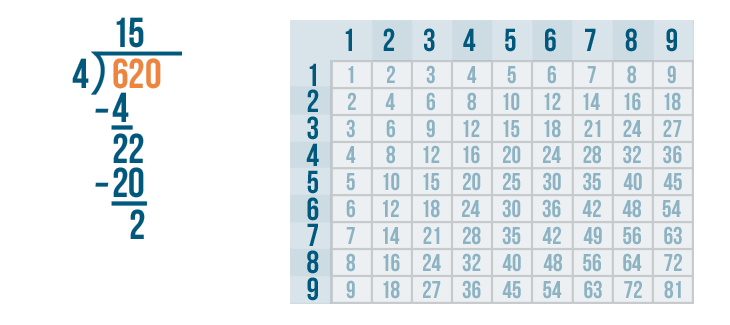
But that changes 62 into a larger number: 620. That won't work.
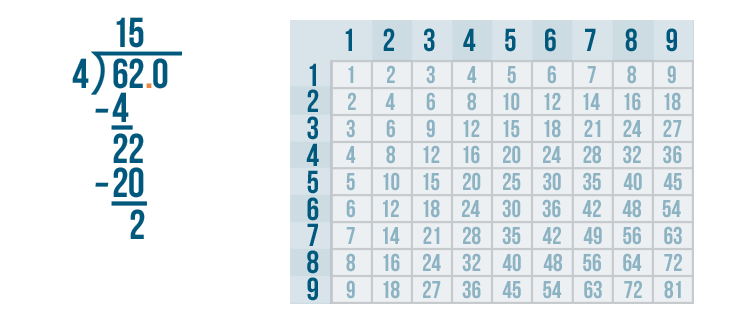
So to keep the value of 62 this same, we'll add a decimal point between the 62 and the 0.
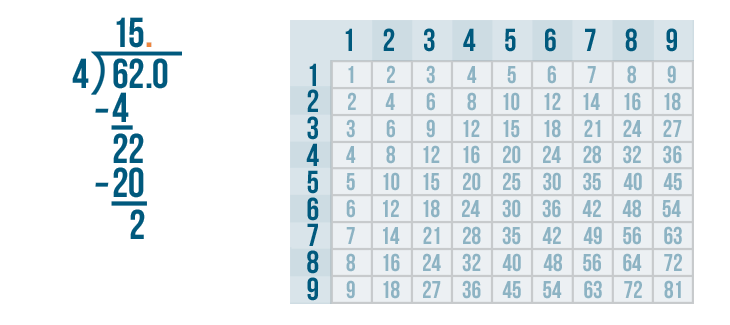
This means our quotient needs a decimal as well. So we'll write a decimal point next to the 15 directly above the other decimal.
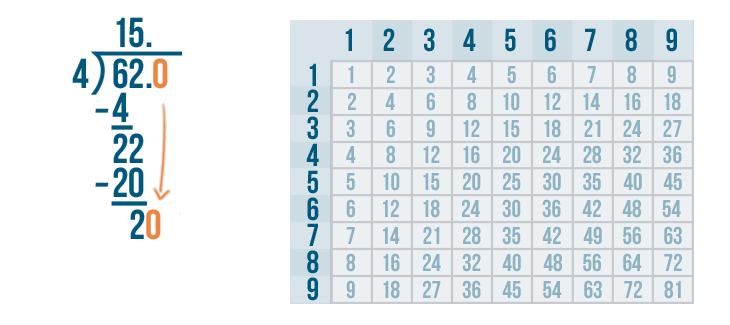
Now we can continue to solve the problem. We'll bring the 0 down and rewrite it next to the 2.
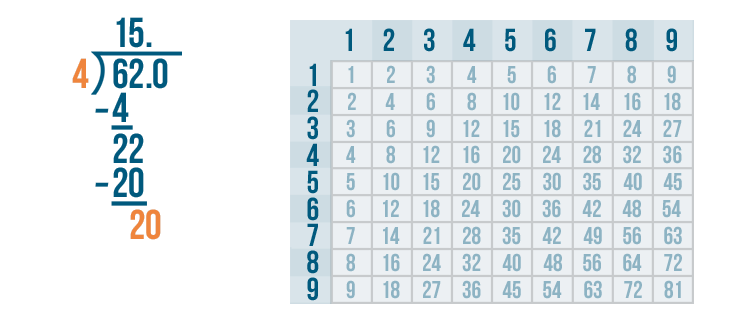
Let's figure out how many times 20 can be divided by 4.
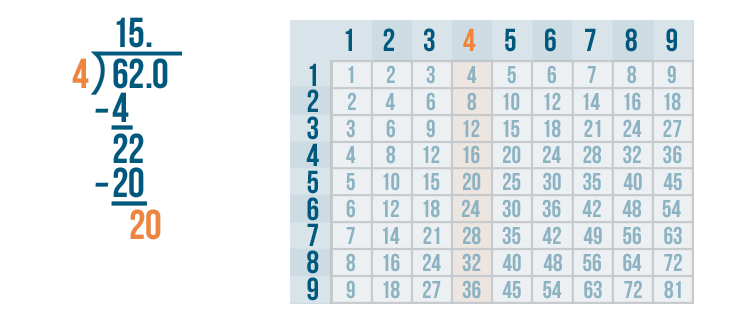
Look at the 4's column. 20 is the number we are dividing, so we'll find the number that is the closest to 20 but not larger than 20.
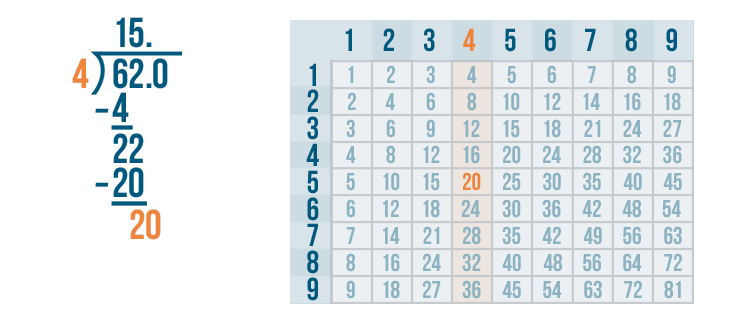
The 4's column has a 20. That's as close as we can get!
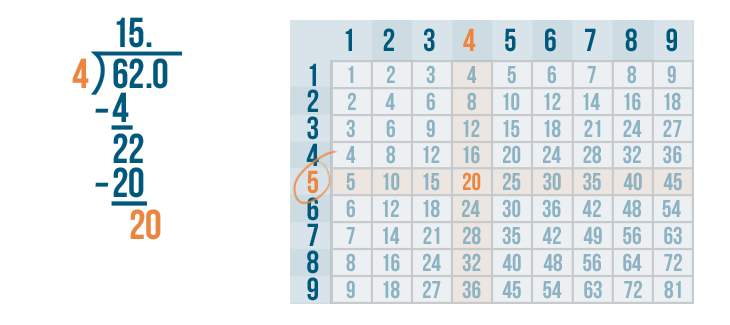
Now we find the row 20 is located in. It's the 5's row. 4 goes into 20 five times.
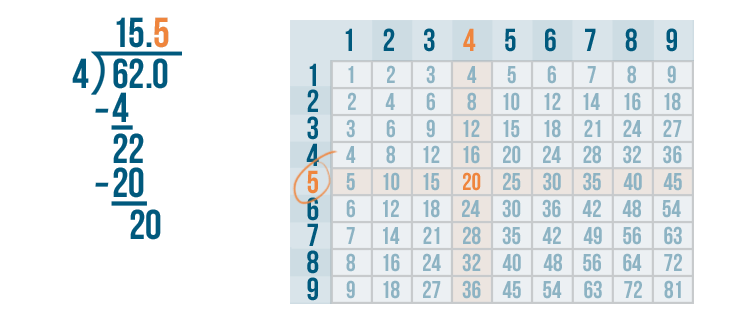
We'll write 5 above the 0.
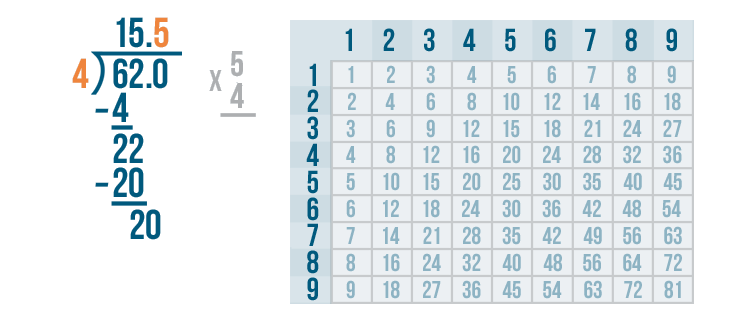
Now it's time to multiply the 5 and 4.
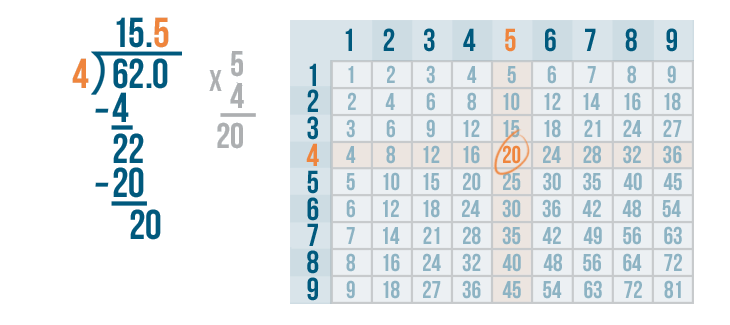
5 x 4 is 20.
Write 20 beneath the 20.
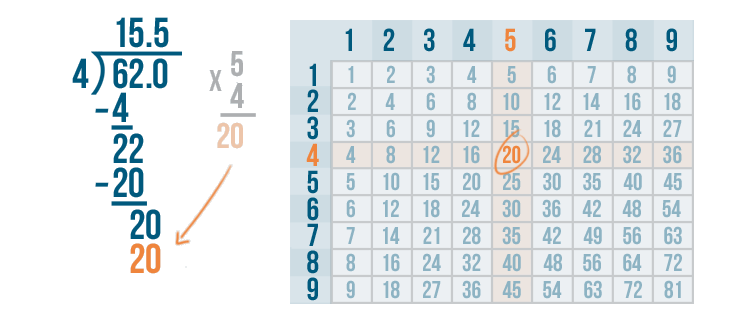
We'll set up our subtraction problem.
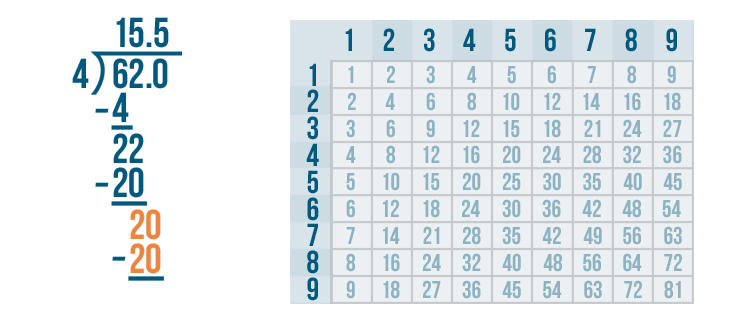
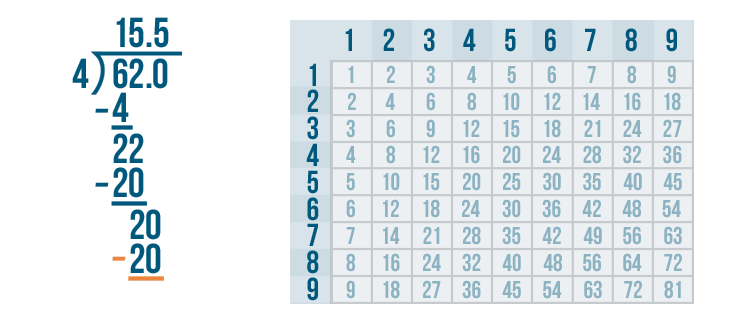
Time to solve 20 - 20.
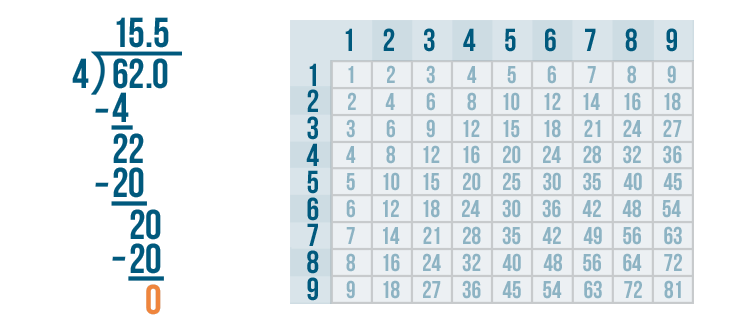
20 - 20 = 0. Write 0 below the line directly below the 0 and 0.
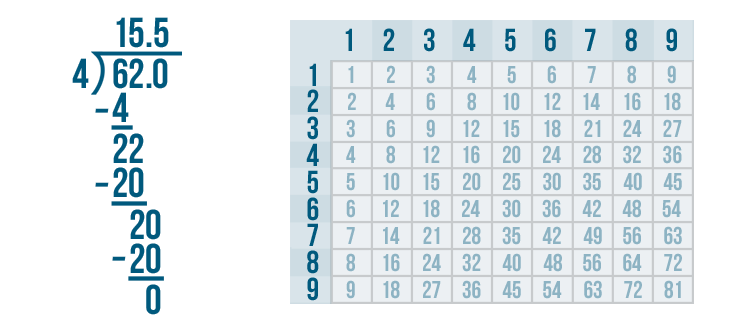
The answer to the subtraction problem is 0. That means we have completed the problem. So 62 / 4 = 15.5.

Sometimes, you may notice that a decimal can start to repeat as you continue to add zeros under the division bracket. This is known as a repeating decimal. When this happens, you can place a horizontal line over the digit that repeats.
Look at the image below. A horizontal line has been placed over the repeating digit.
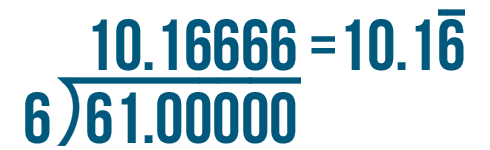
Another way to handle a repeating decimal is to round it. Rounding creates a new number that has a value close to the original number.
When rounding a repeating decimal, you'll reduce the number of digits that come after the decimal point. First, decide which digit you are rounding to. Then look at the digit to the right of it. If the digit is 5 or more, increase the rounded digit by 1. If it is 4 or less, the rounded digit stays the same. The other digits after the rounded digit are not written.
Look at the image below. In this case, each of these repeating decimals has been rounded to the second digit after the decimal point.

Try this!
Find the decimal quotient for each of the long division problems below.
Checking your work
Checking your work after you divide is a good habit to develop. Checking helps you know that your answer is correct. To check the answer to a division problem, you'll need to use multiplication.

Let's look at this problem: 54 / 6 = 9.
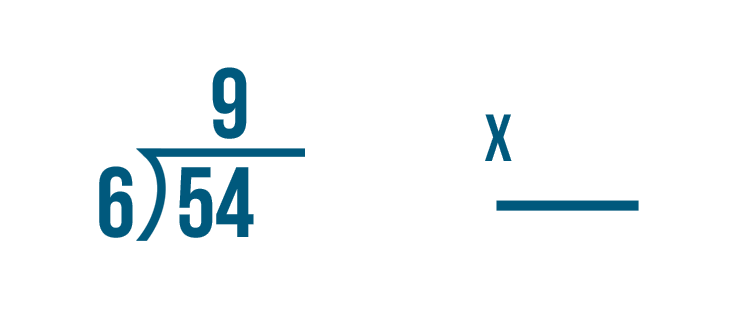
How do we know that 9 is the correct answer? We can check by multiplying.
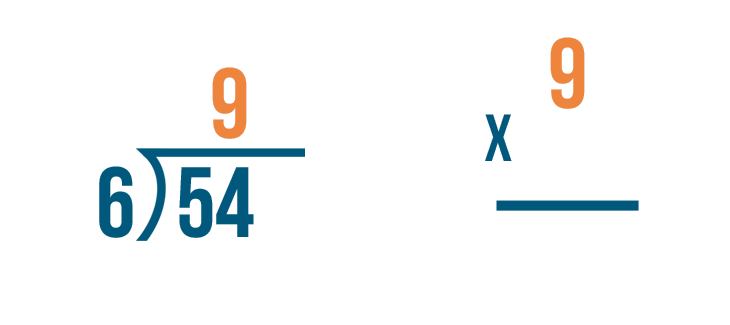
Let's set up our multiplication problem. First, we'll write the quotient. That means we'll write 9.
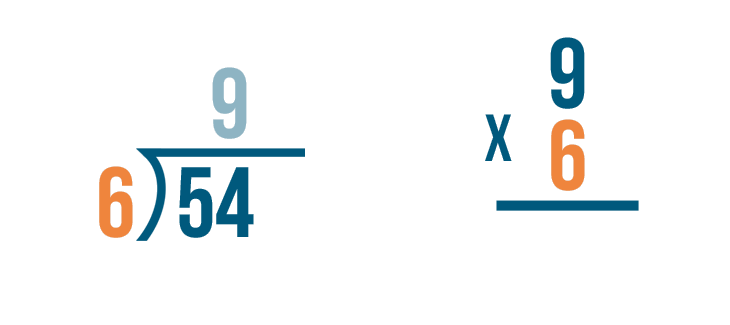
Next, we'll multiply the number that we divided by, 6.
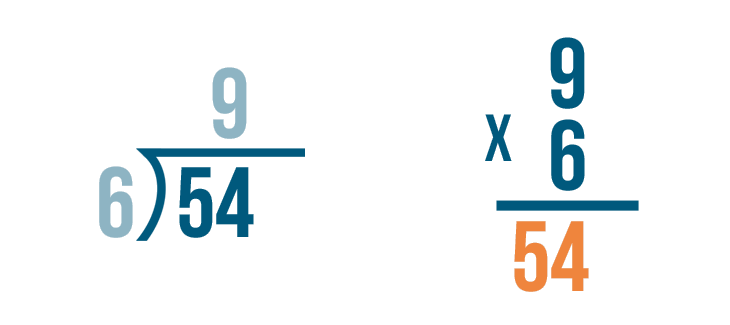
Time to multiply. 9 x 6 = 54.
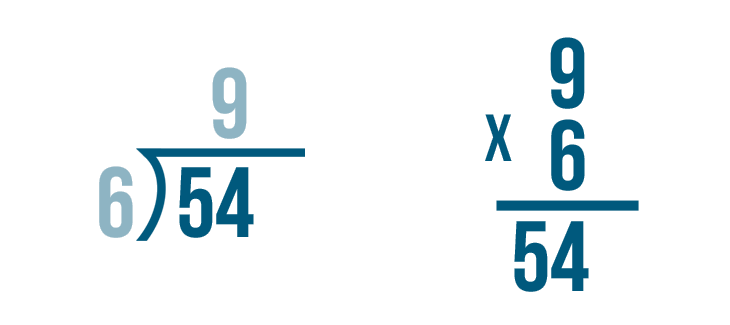
If we divided correctly, the answer will match the larger number in the division problem.
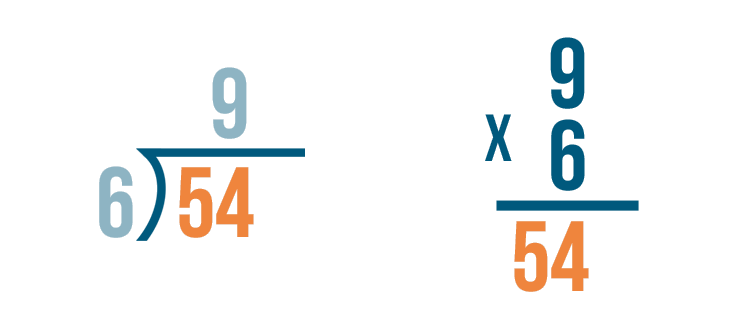
They are both 54. We checked the problem, and it was correct!
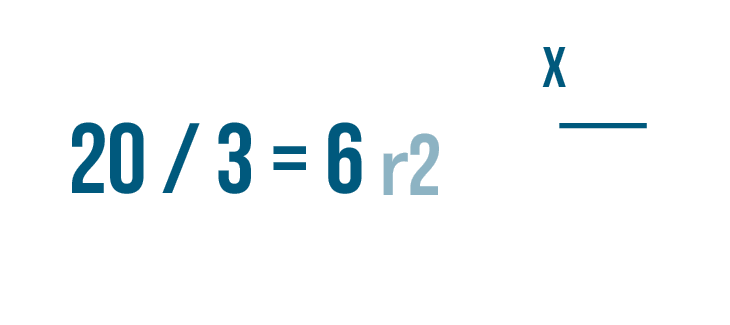
Let's try checking another problem. This time, the quotient has a remainder: 20 / 3 = 6 r2.
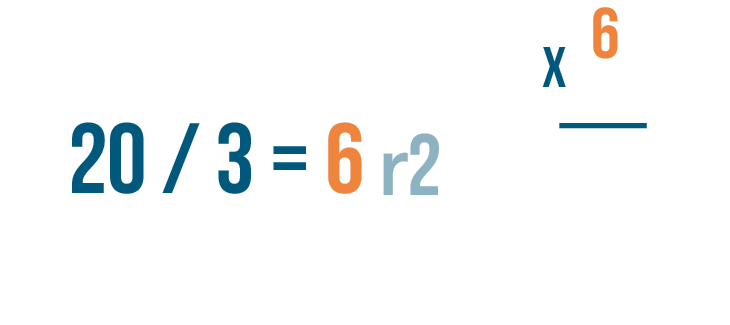
Let's set up our multiplication problem. First write the quotient without the remainder. That's 6.
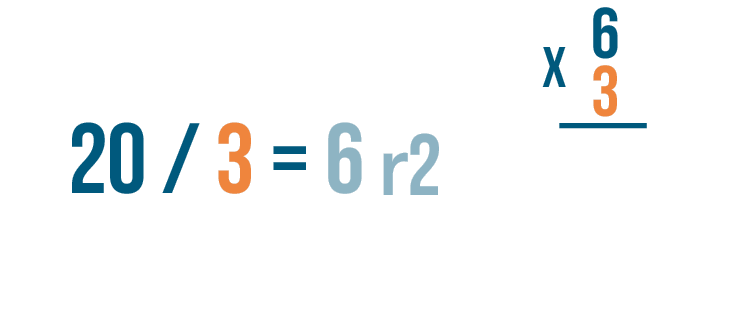
Then multiply the amount that the larger number was divided by, 3.
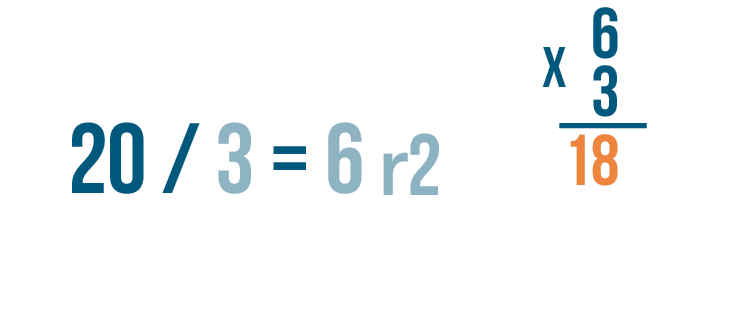
Now it's time to multiply. 6 x 3 = 18.
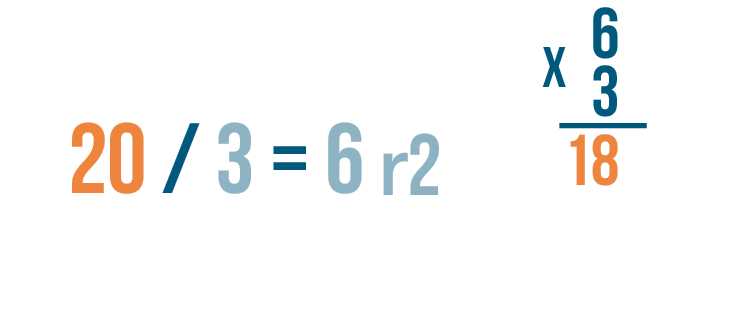
Let's check to see if our answer matches the larger number in the division problem — 18 and 20. No, they aren't equal.
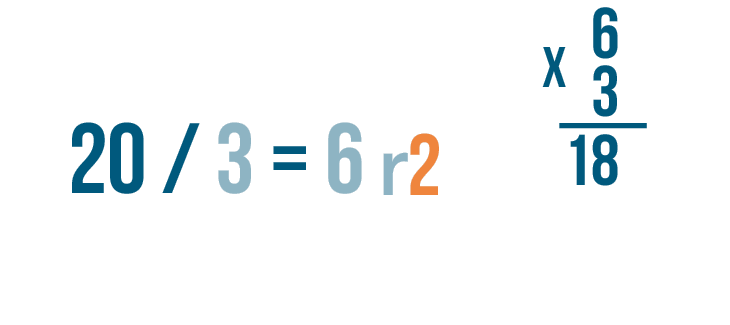
That may be because we haven't included the remainder, 2.
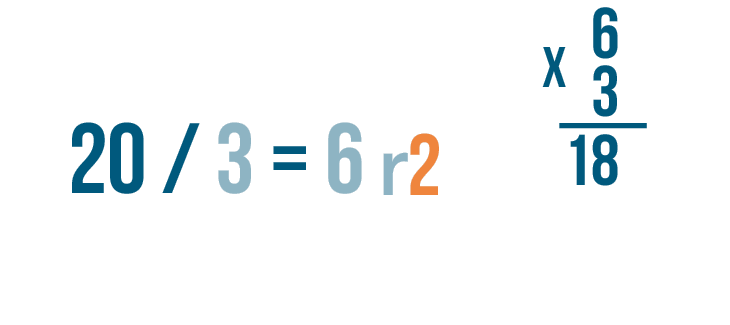
Since the answer to the division problem has a remainder...
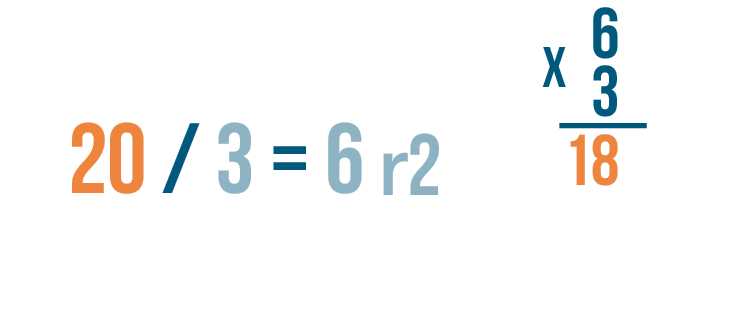
Since the answer to the division problem has a remainder... just multiplying should give you a number less than the original number.
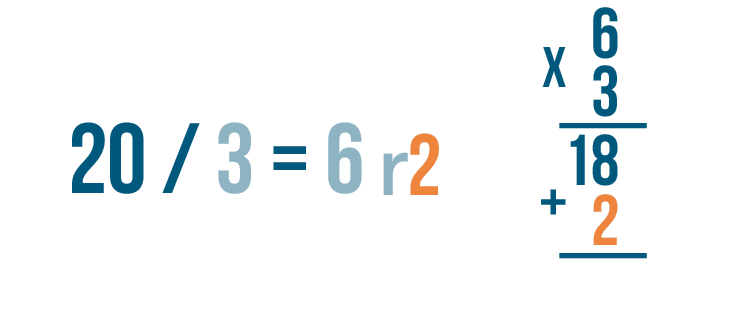
We'll set up an addition problem to add the 2 to 18.
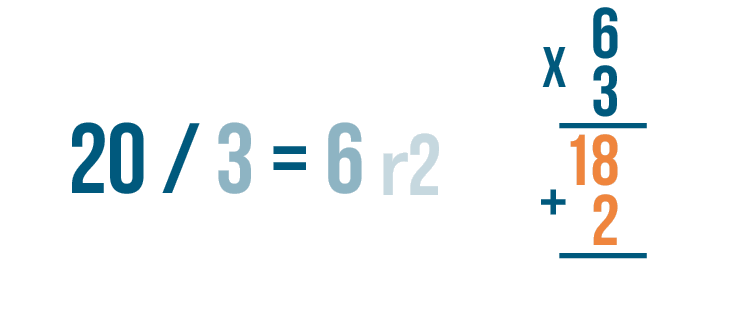
Now add 18 and 2.
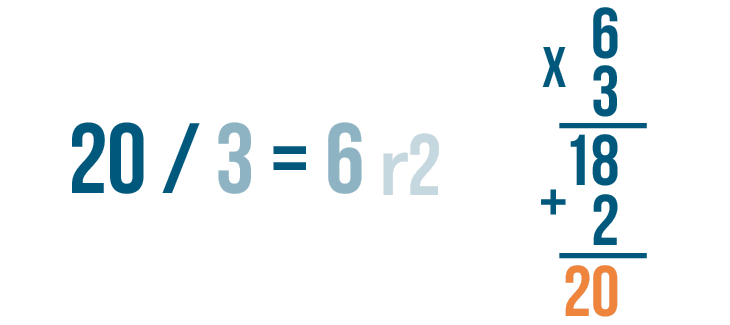
18 + 2 is 20.
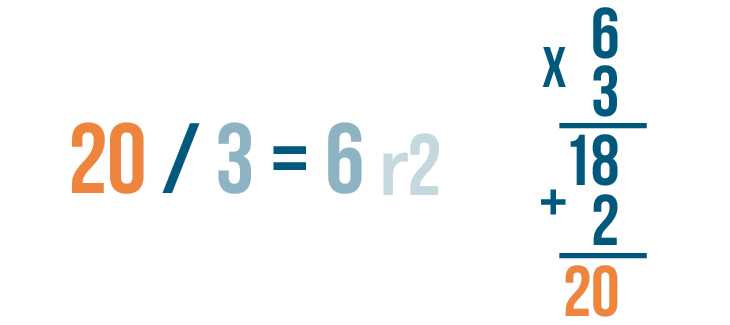
Finally, check to see if 20 matches the larger number in the division problem. It does!

In the slideshow, we used multiplication to check our division. The answer to the multiplication problem should always be the same as the larger number in the division problem. If your two answers don't match, check to see if you added the remainder. If your answers are still different, you might have made a mistake the first time you were dividing. Try solving the problem again.
Long division with decimals
In this lesson, you also learned how to solve division problems that have a decimal in the answer. Checking your work for this type of problem is similar to checking other division problems. You'll follow the same steps.
We'll try checking this problem: 57 / 5 = 11.4.
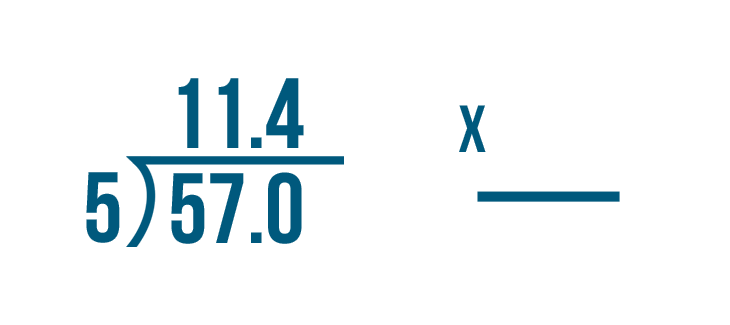
Let's set up our multiplication problem.
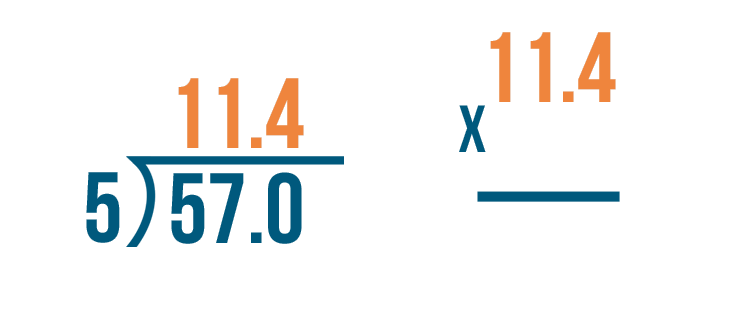
We'll write the decimal quotient, 11.4.
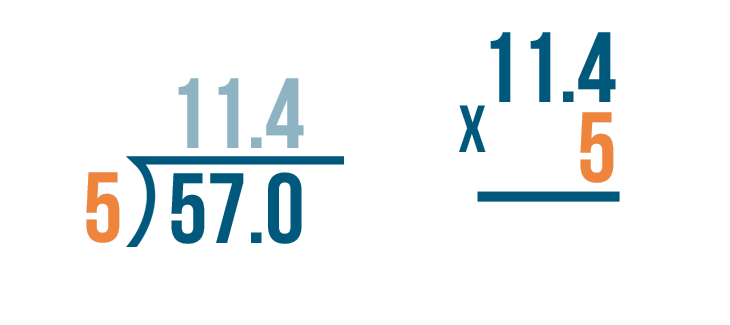
Next, we'll multiply the number that we divided by, 5.
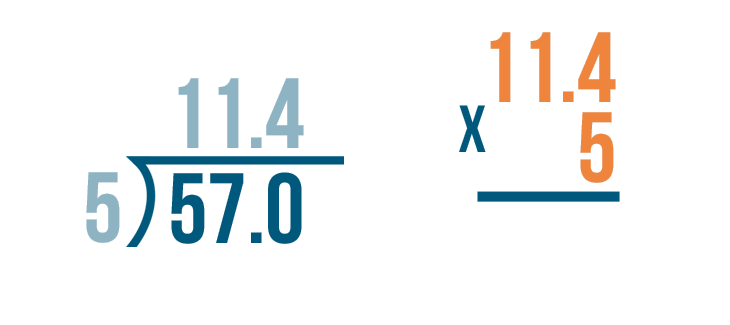
Now it's time to multiply: 11.4 x 5.
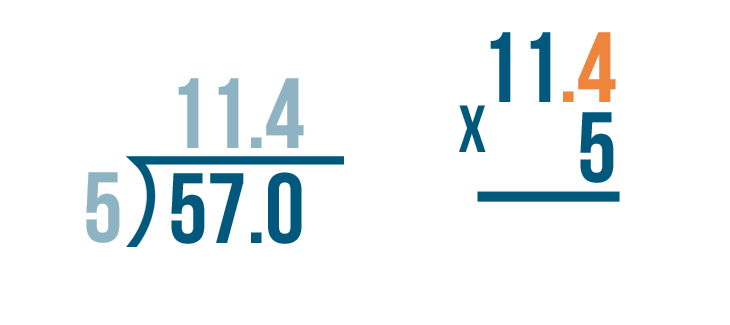
Since the quotient had one digit to the right of the decimal point...
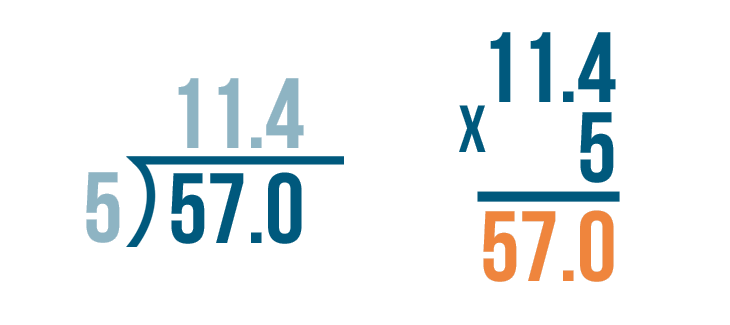
Since the quotient had one digit to the right of the decimal point... we write the answer with one digit to the right of the decimal point. 11.4 x 5 = 57.0.
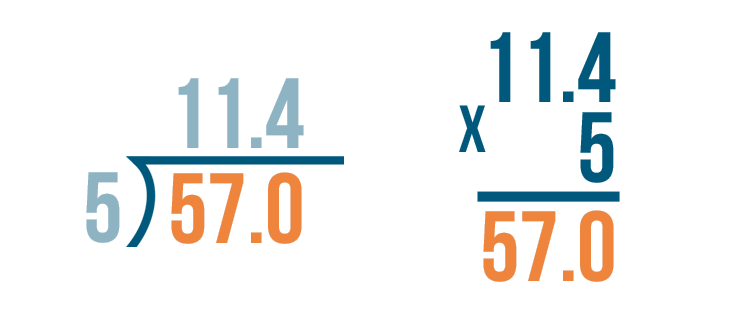
Finally, we'll check to see if 57.0 matches the larger number in our division problem. They are the same. Our answer was correct.

Practice!
Practice division by solving these problems. There are 3 sets of problems. Each set has 5 problems.
Set 1
Set 2: Type your answer using remainders.
Set 3: Type your answer using decimals.
/en/multiplicationdivision/video-division/content/