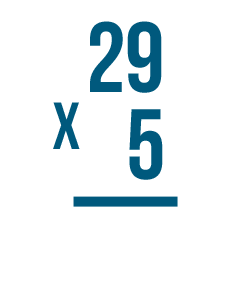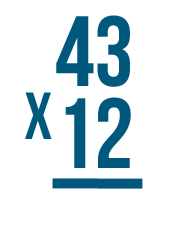Lesson 2: Multiplying 2- and 3-Digit Numbers
/en/multiplicationdivision/introduction-to-multiplication/content/
Stacked multiplication problems
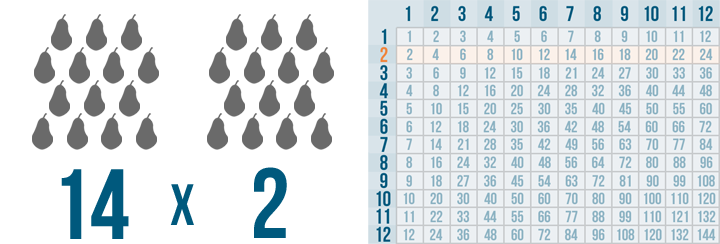
When you multiply a number or amount, you're increasing it many times. In Introduction to Multiplication, you learned that multiplication can be a way to understand things that happen in real life. For instance, imagine that a store sells boxes of pears. The small boxes contain five pears each. You buy two. You could write the situation like this, and use the times table to solve it:
Now, imagine that you decide to buy two larger boxes containing 14 pears each. That situation would look like this:
This problem is harder to solve. Counting the pears would take a while. Plus, there's no 14 on the times table. Fortunately, there's a way to write the problem so that you can break it into smaller pieces. It's called stacking. It means that we'll write the numbers on top of one another instead of side by side.
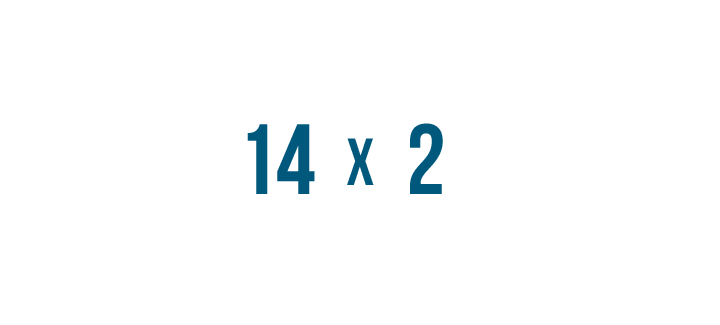
Let's practice stacking with this problem, 14 x 2.
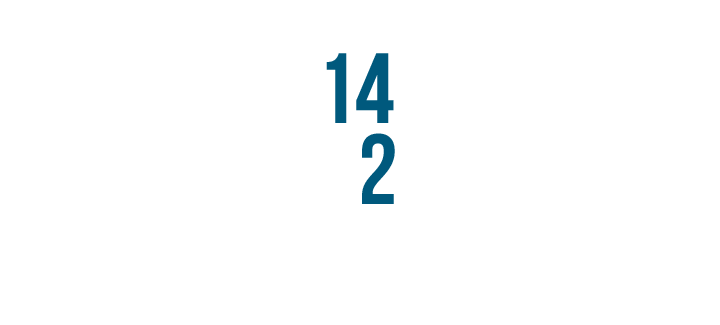
First, write the numbers, one above the other. It's a good habit to always write the larger number on top. The problem will be harder to solve if you don't.
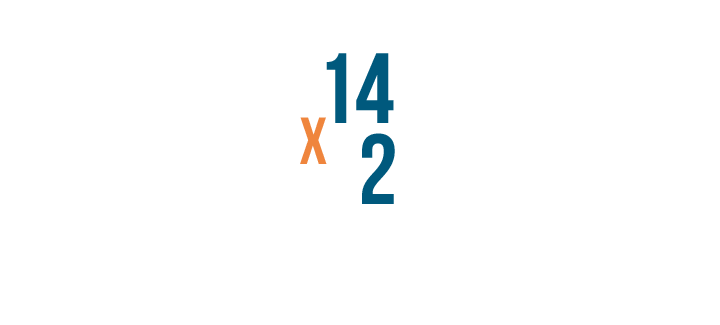
Next, write the times sign to the left of the numbers.
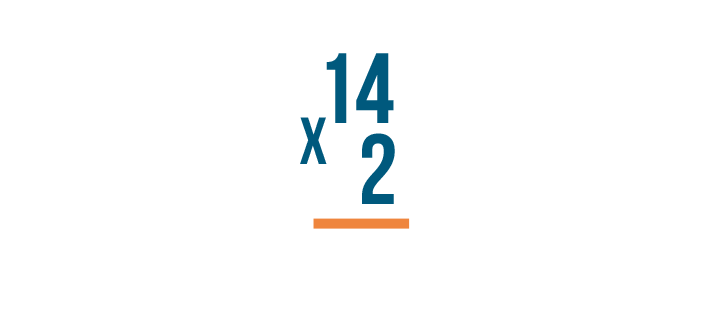
Instead of an equals sign, put a line underneath the number on the bottom.
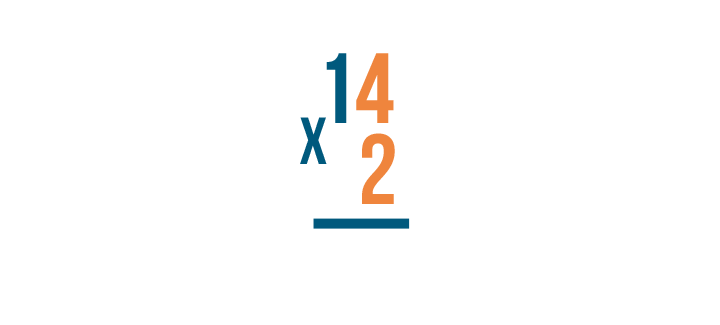
Notice how the numbers are lined up to the right?
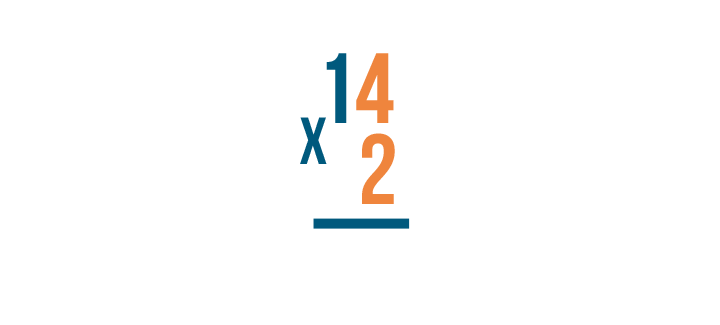
When you write a stacked multiplication problem, always make sure the numbers are lined up this way.
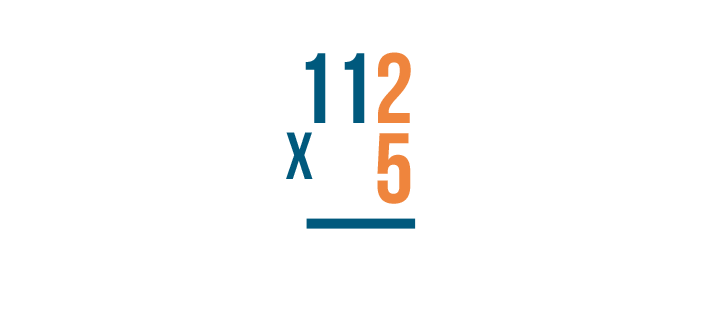
For example, let's look at another problem, 5 x 112. See how the 2 is right above the 5?
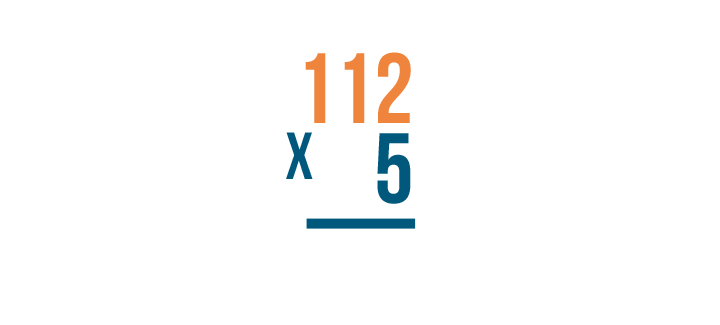
Also, notice that we put the larger number on top, even though it was the second number in our original expression.
Always set up stacked multiplication problems the same way: with the larger number on top...
Always set up stacked multiplication problems the same way: with the larger number on top... and the right digits lined up.

Solving stacked multiplication problems
At first glance, stacked multiplication problems might look pretty complicated. Don't worry! If you can solve the problems in Introduction to Multiplication, you can learn to solve these problems too. To multiply large numbers, you'll use the same basic skills you use to multiply small ones. You can even use the same tools, like times tables.
Let's see how solving stacked multiplication problems works.
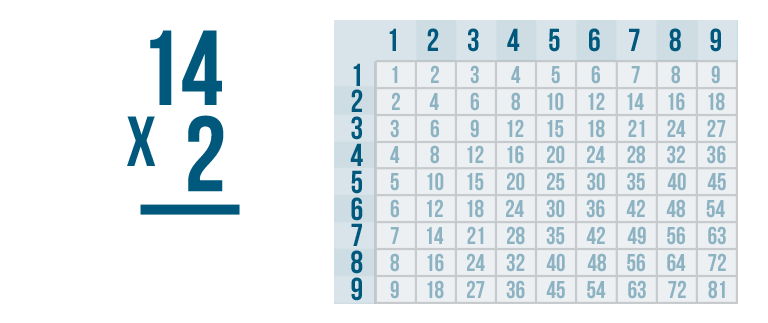
Remember the example of two boxes that each had 14 pears each? To find out how many pears there are total, we'll solve this problem: 14 x 2.
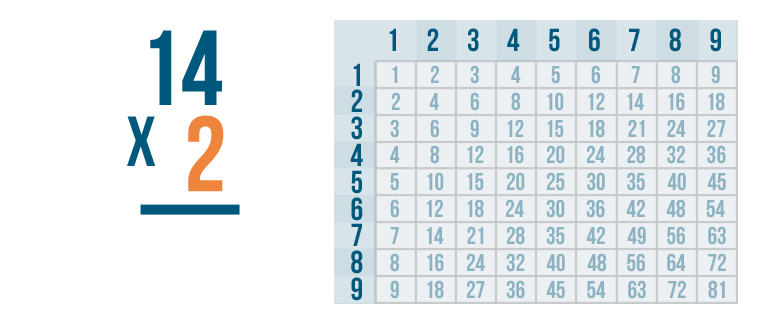
When you multiply stacked numbers, you start with the right digit in the bottom number of the problem. Our bottom number only has one digit: 2.

We'll multiply 2 by the top number, 14. Since there's no 14 in the times table, we'll have to multiply one digit at a time.
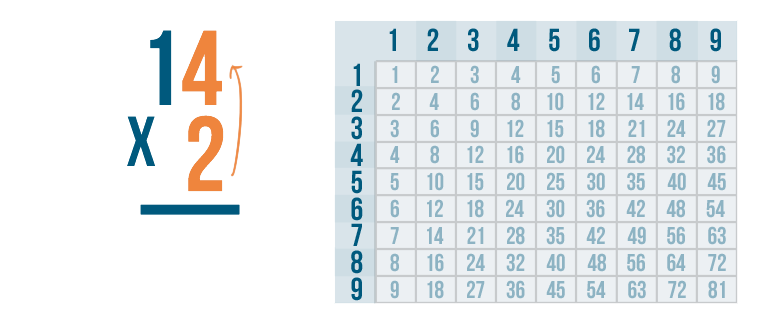
As usual, we'll solve the problem from right to left. So, we'll multiply 2 by the digit on the top right. Here, that's 4.
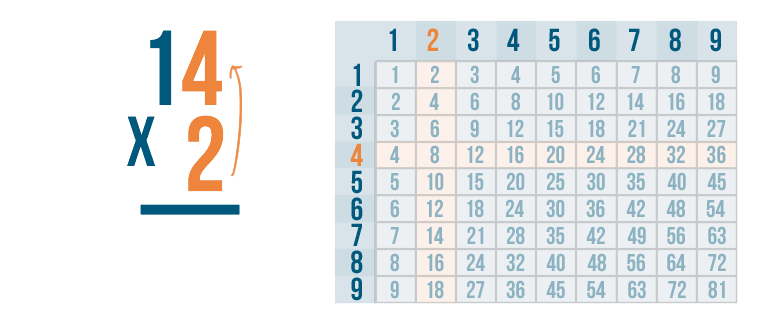
Now it's time to solve 2 x 4. We can use the times table.
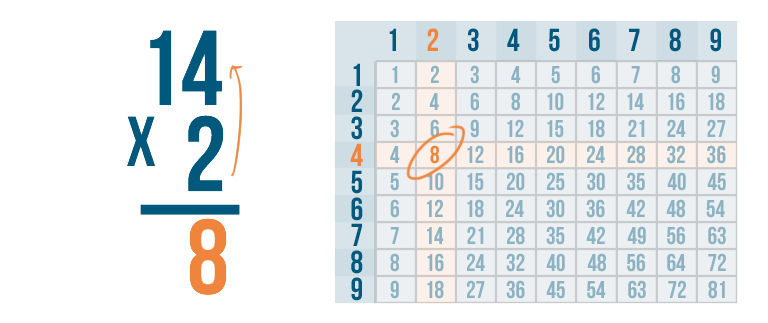
2 x 4 is 8. We'll write 8 below the 2 and 4.
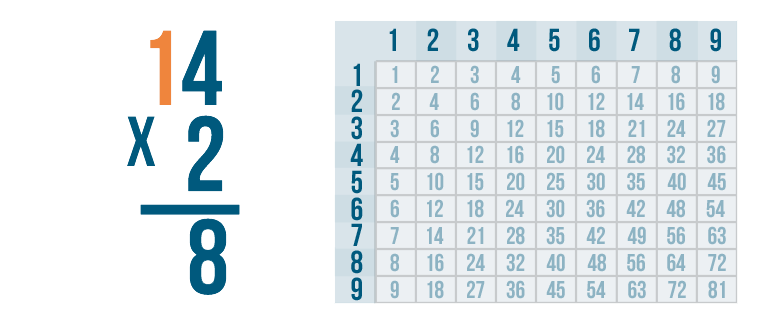
Now we'll multiply 2 by the next digit to the left: 1.
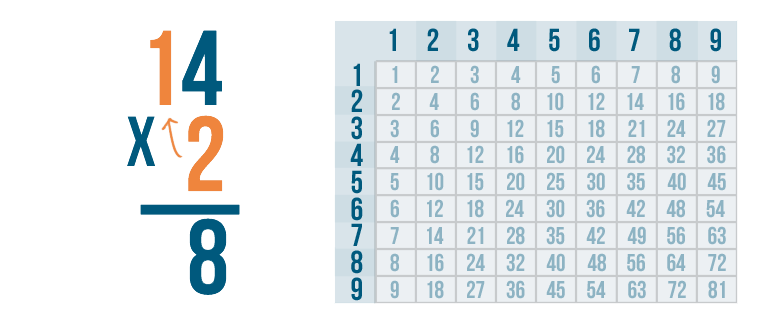
Now we solve 2 x 1.
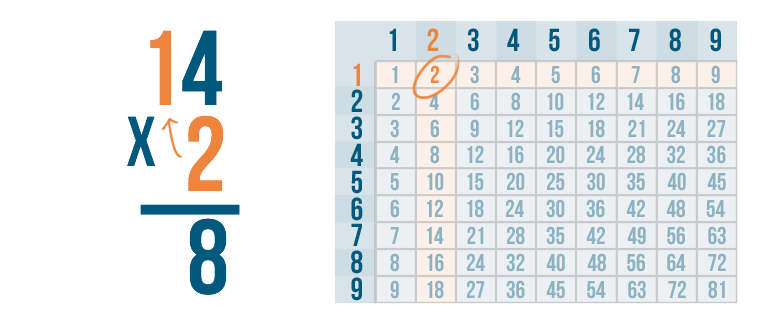
Whenever you multiply a number by 1, that number stays the same. So 2 x 1 is 2. Just to be sure, we'll check the times table.
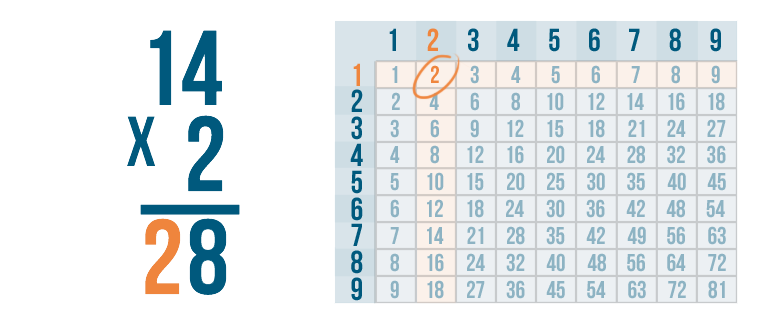
Write the 2 beneath the line, directly below the 1.
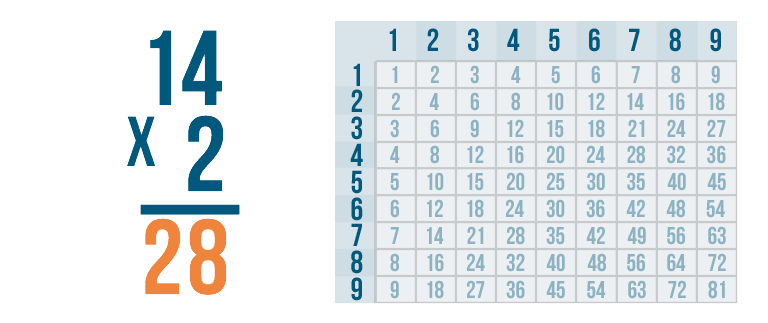
We're done! Our total is 28, or twenty-eight. 14 x 2 = 28.
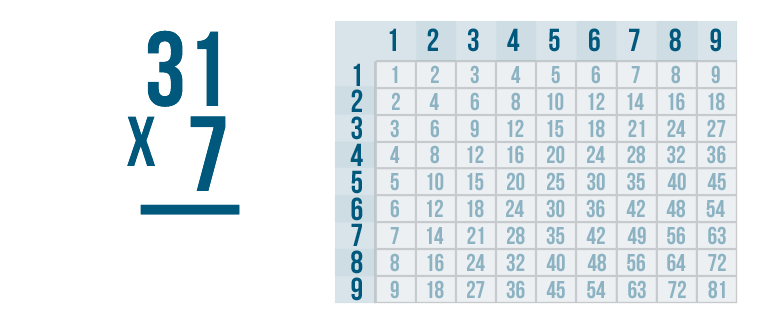
Let's practice with another problem, 31 x 7.
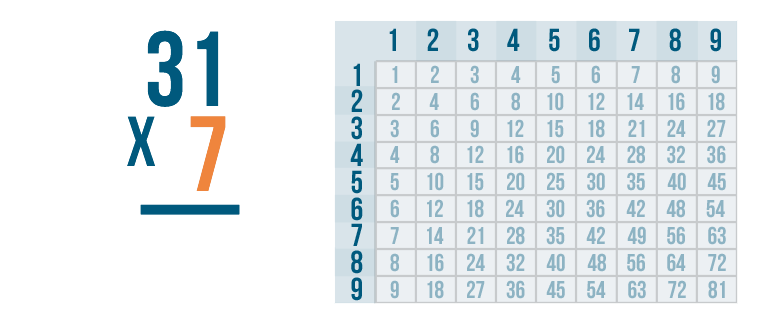
Always start with the digit on the bottom right. Here, that's 7.
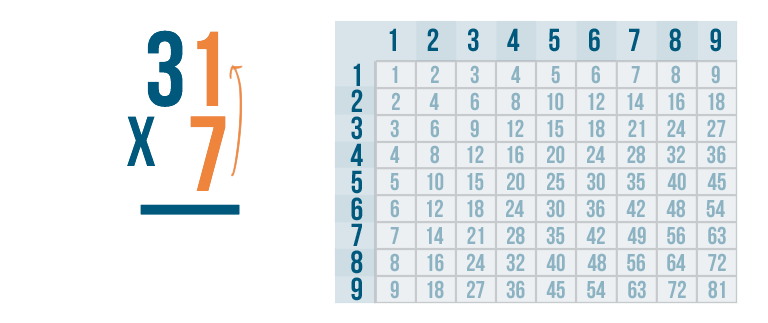
First, multiply 7 by the digit on the top right, 1.
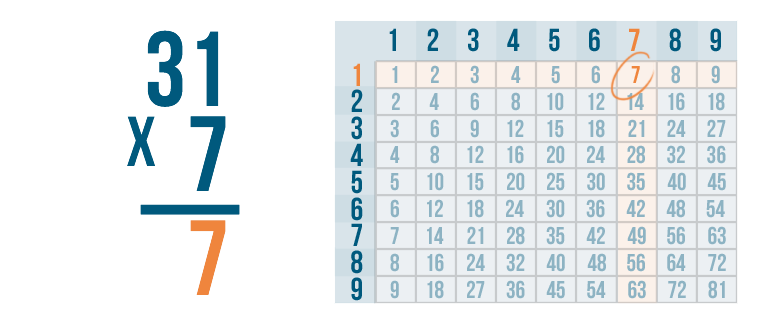
7 x 1 is 7. Write the 7 directly below the digits we just multiplied.
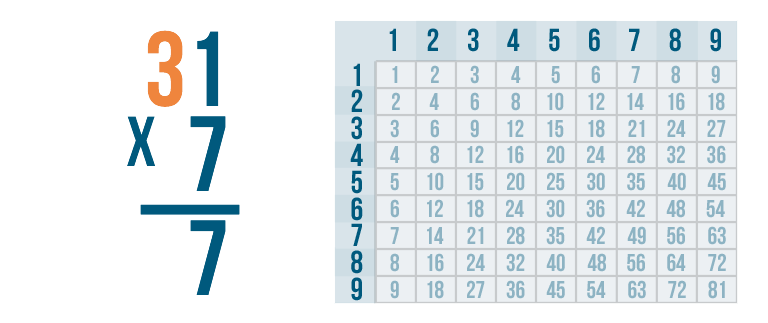
Next, we'll multiply 7 by the next digit to the left. That's 3.
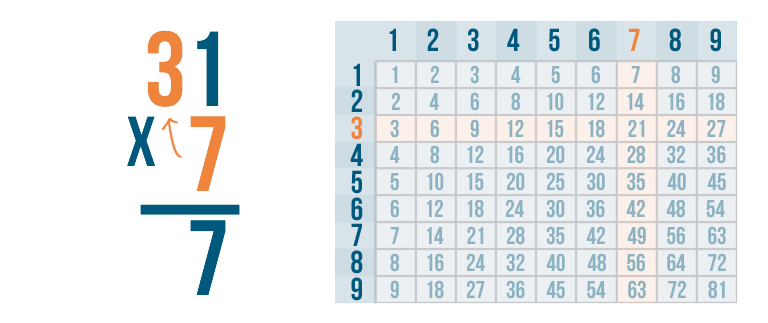
We'll use the times table to solve for 7 x 3.
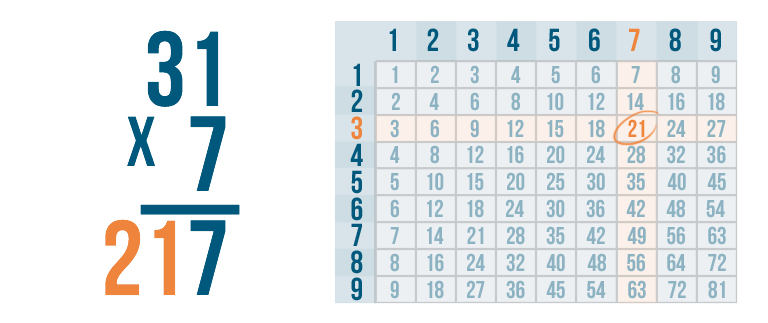
7 x 3 is 21. Make sure to line the numbers up so that the right digit of 21, 1, is directly under the 3.
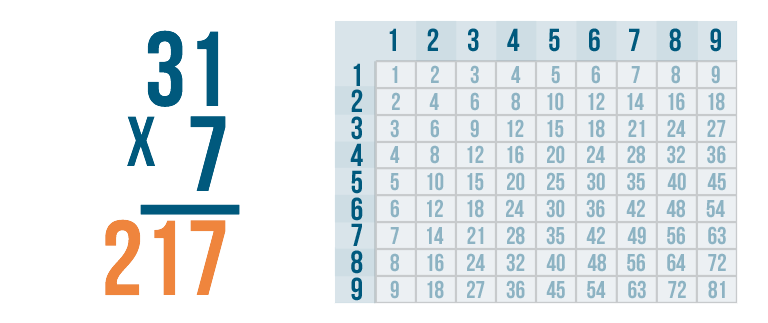
Our answer is 217. So, 31 x 7 = 217.

Try this!
Stack and solve these multiplication problems. Then, check your answer by typing it into the box.
Using carrying
On the last page, you practiced multiplying vertically stacked numbers. Some problems need an extra step. Let's look at the following problem:
If you try to multiply 9 x 5, you might notice that there is no room to write the product, 45. When the product of two numbers is greater than 9, you'll need to use a technique called carrying. If you know how to add large numbers, you might remember using carrying in addition too. Let's see how it works in multiplication.
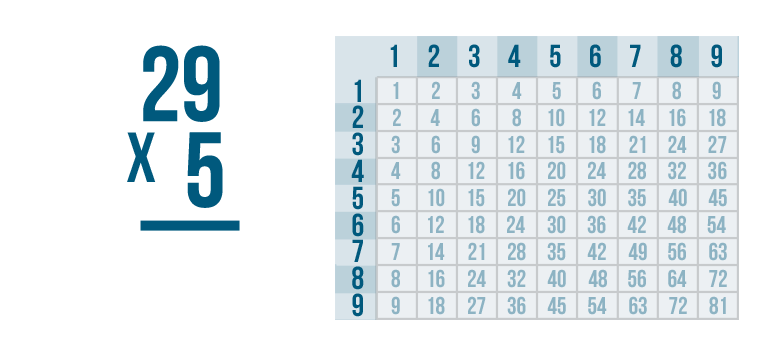
Let's try the problem we just looked at, 29 x 5.

As usual, we'll start by multiplying the 5 by the top-right digit, 9.

According to our times table, 5 x 9 is 45, but there's no room to write both digits underneath the 5 and 9.
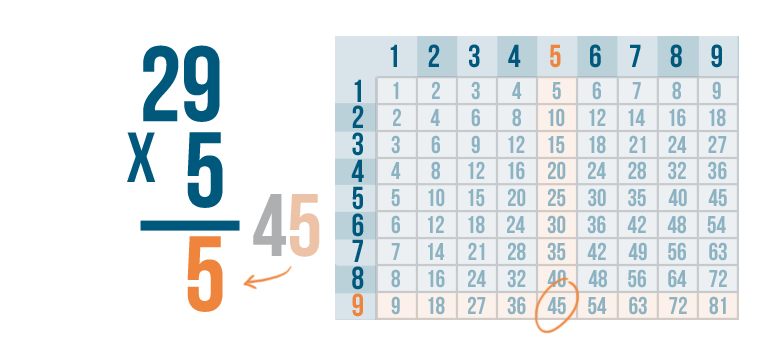
We'll write the right digit, 5, under the line...
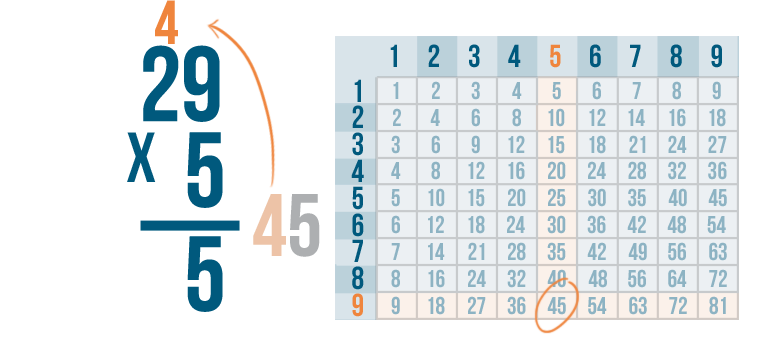
We'll write the right digit, 5, under the line...then we'll carry the left digit, 4, up to the next set of digits in the problem.

See how it works? We multiplied 5 and 9 to get 45. We put the 5 underneath the line, carried the 4 and placed it above the next set of digits.
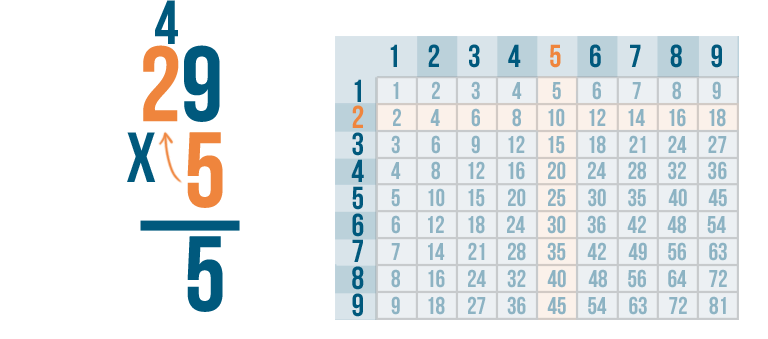
Now it's time for the next step. It's the same as with any other multiplication problem. We'll multiply 5 x 2.
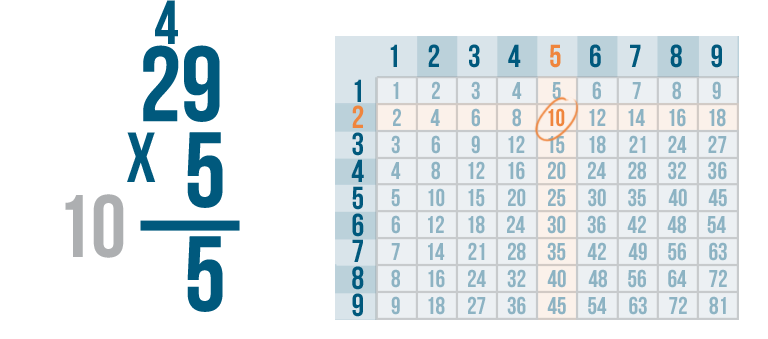
5 x 2 = 10. However, we won't write 10 under the line yet - there's one more step.
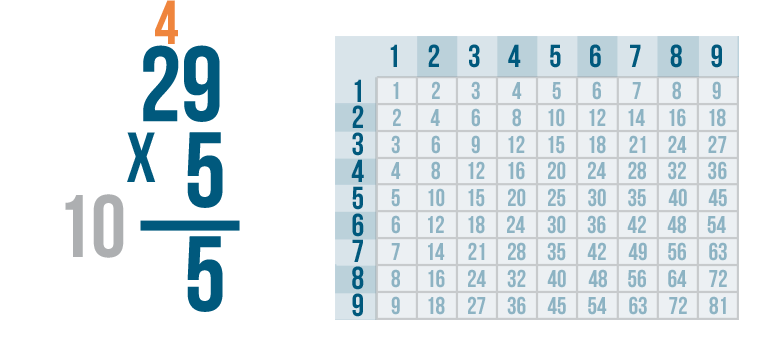
Remember the number we carried, 4?
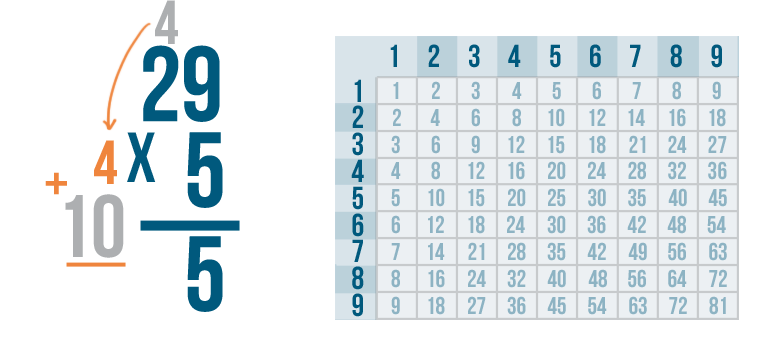
We have to add it to our product, 10.
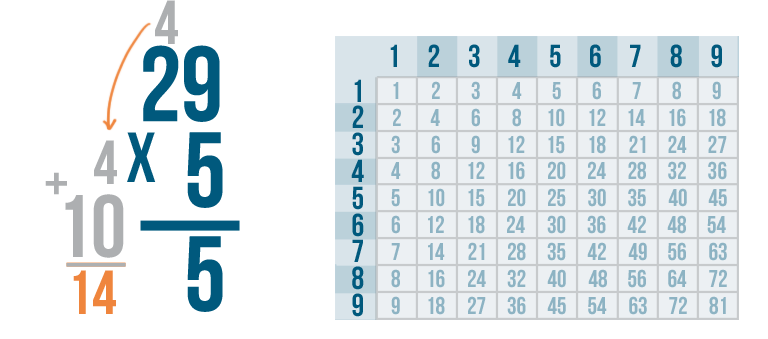
4 + 10 is 14.
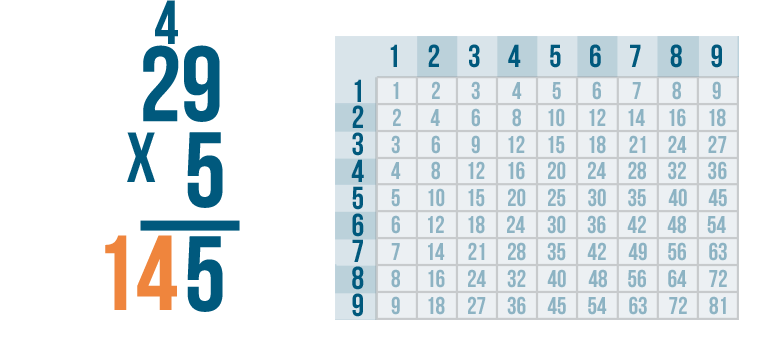
We'll write 14 beneath the line.
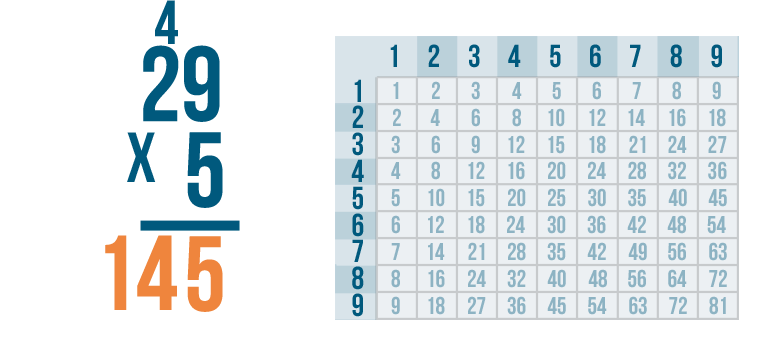
Our total is 145. We now know that 29 x 5 = 145.

Let's try another problem, just for practice. 208 x 6.

First, we multiply the bottom number, 6, by the digit on the top right. That's 8.

6 x 8 is 48.

We'll write the 8 under the line...
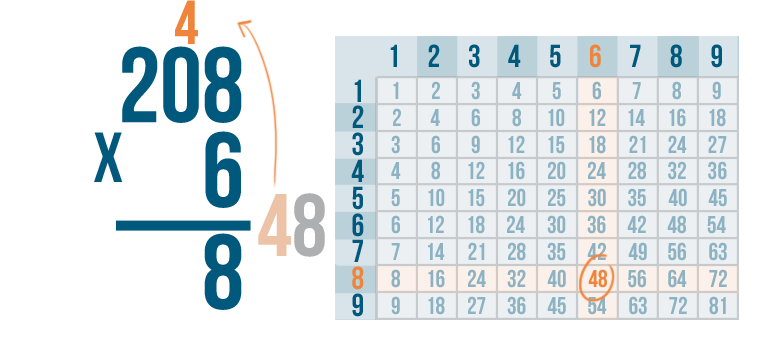
We'll write the 8 under the line...and carry the 4. We'll place it above the next digit.

The next digit is 0.

Anything times zero is 0, so we know that 6 x 0 = 0.

Remember, we don't write that 0 beneath the line yet. We have to add it to the 4 we just carried.

4 + 0 = 4. We'll write 4 beneath the line.

Finally, we multiply 6 and 2.

6 x 2 = 12, so we'll write 12 beneath the line.

We're done! The answer is 1248, or one thousand, two hundred and forty-eight. 208 x 6 = 1248.
Try This!
Stack and solve these multiplication problems. Then, check your answer by typing it into the box.
Multiplying large numbers
On the past few pages, you've practiced multiplying large numbers with small ones. What happens when you have to multiply two large numbers?
For example, imagine that your cell phone bill is $43 a month. There are 12 months in a year, so to find out how much you pay for your phone every year, you could solve for 43 x 12. You'd write the expression like this:
This problem might look hard at first, but don't worry. If you can multiply small numbers, you can multiply large ones too. All you have to do is divide this large problem into a few smaller ones. As always, you can use your times table to help.
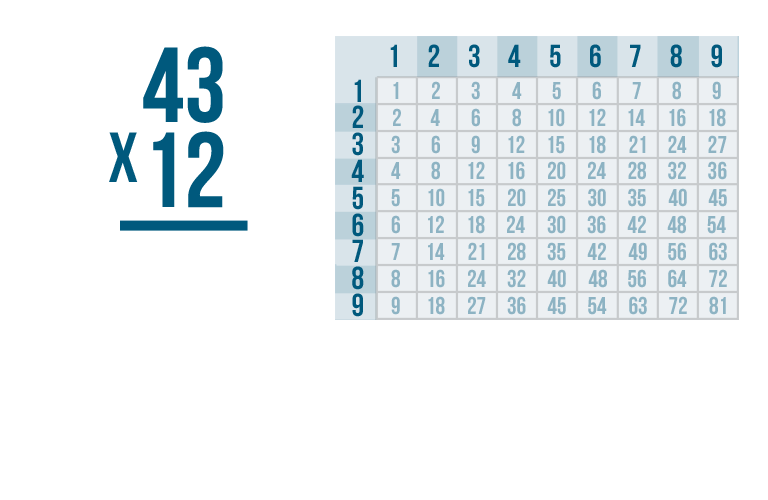
To solve a large problem like this, start with the same steps you use to solve any other multiplication problem.
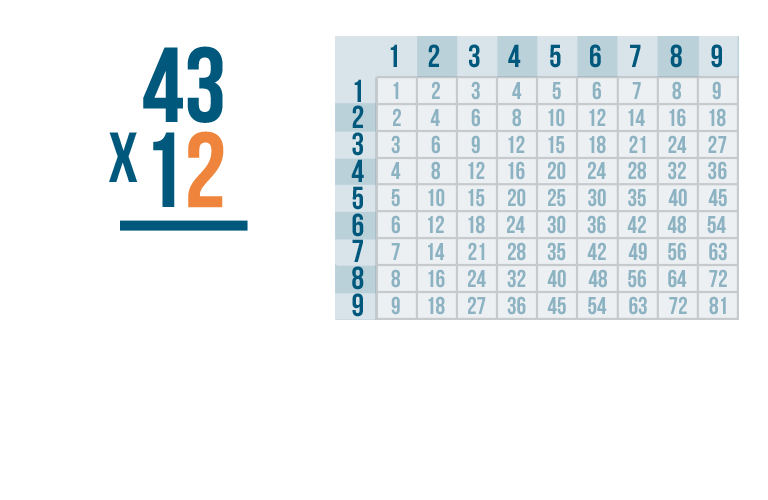
As always, you start with the digit on the bottom right. Here, that's 2.
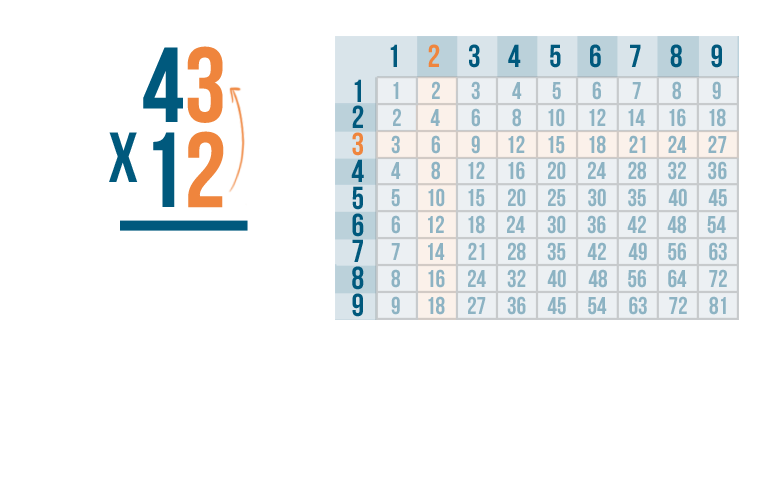
We'll multiply it by the digit on the top right, 3.
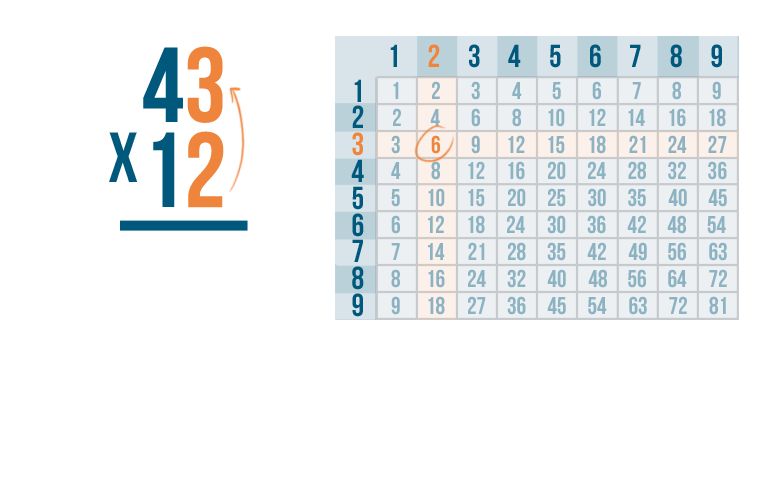
Thanks to our times table, we know that 3 x 2 is 6.
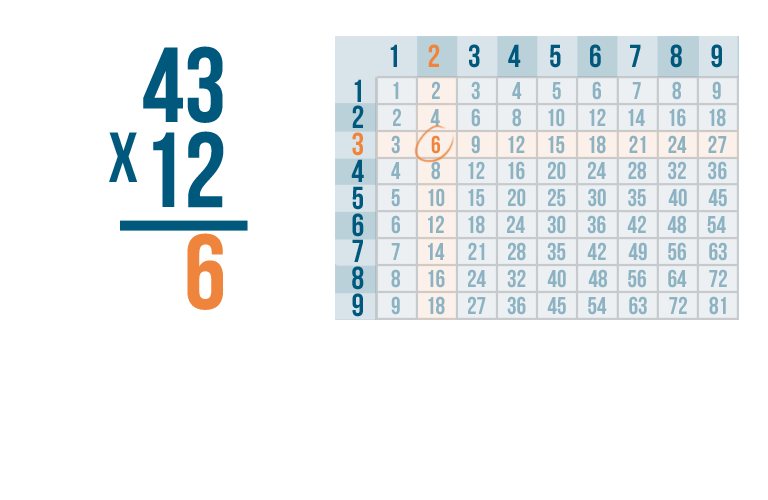
We'll write the 6 beneath the line, to the far right.
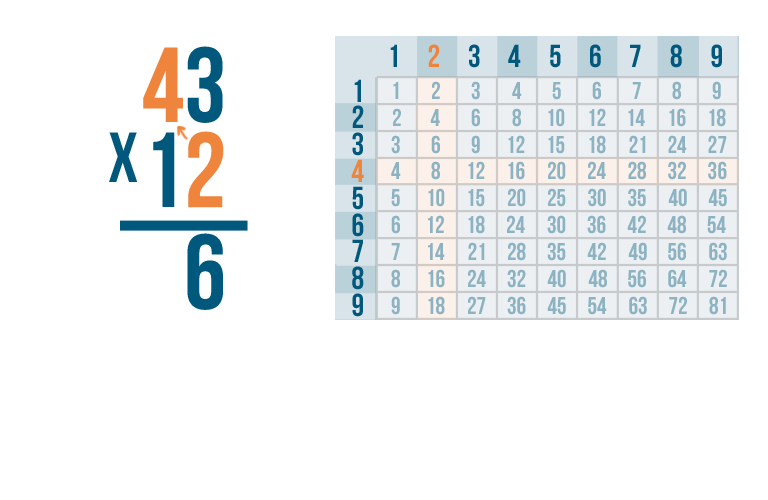
Next, we'll multiply 2 x 4.
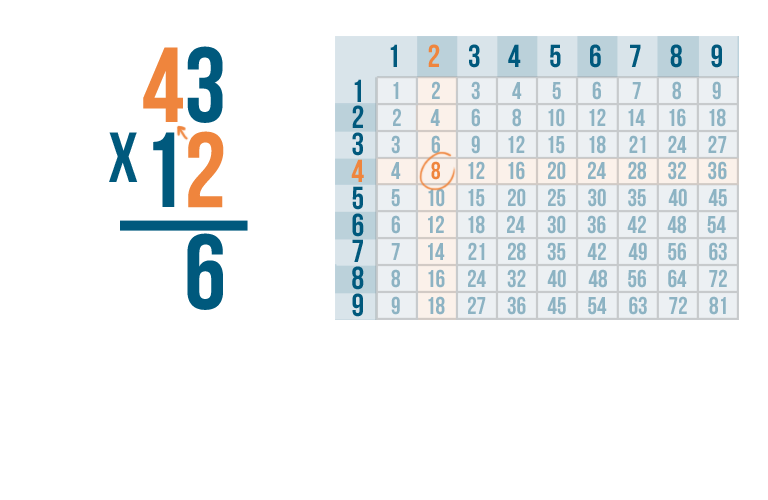
2 x 4 is 8.
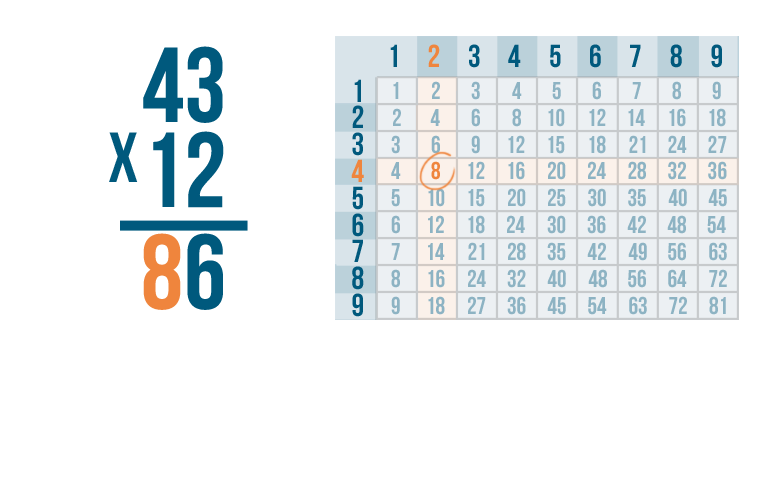
Write 8 below the line, right under the 4.

OK. The first half of the problem is done.
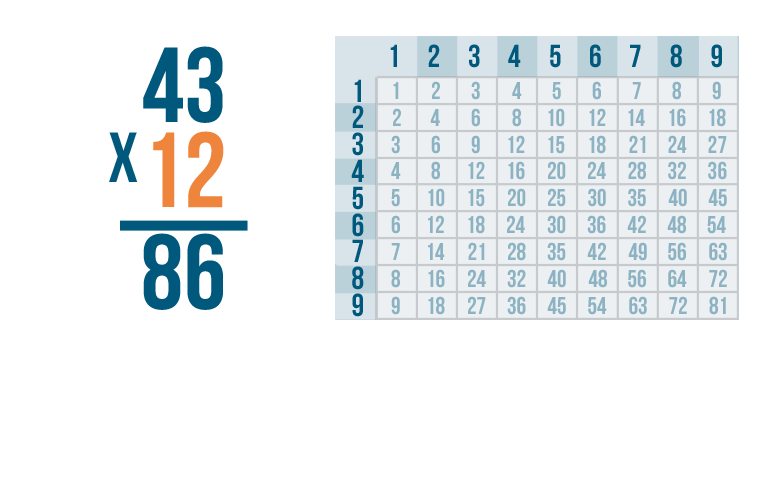
Now it's time to look at the bottom number again.
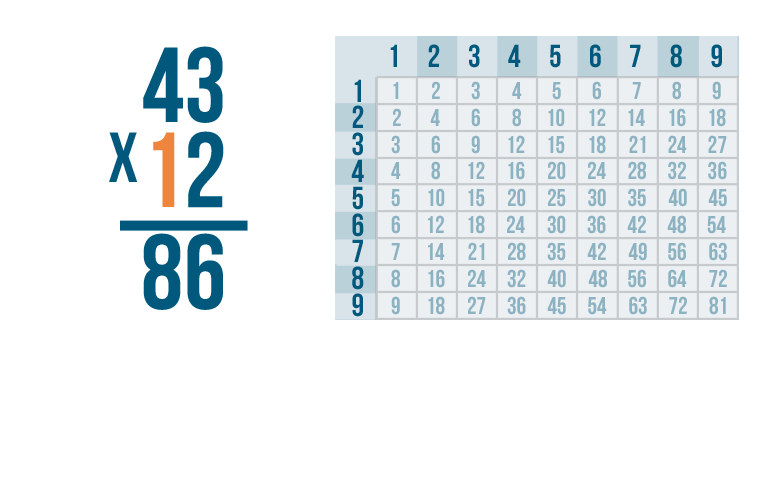
We're going to multiply the next digit. That's 1.
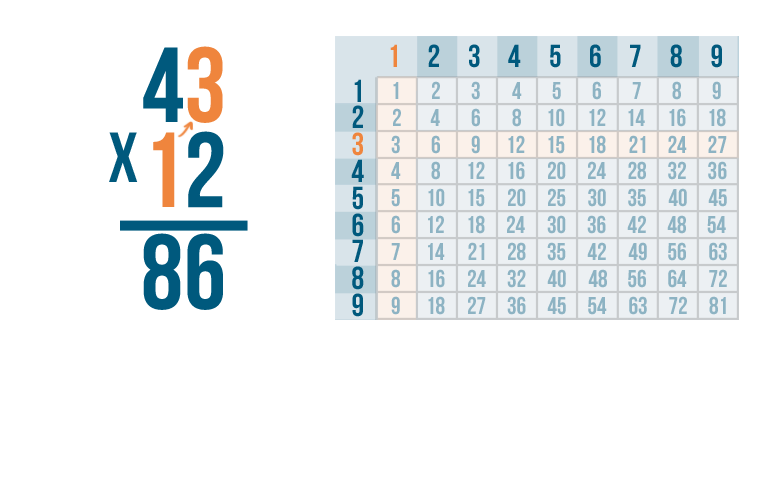
First, multiply 1 by the top number on the right. Here, that's 3.
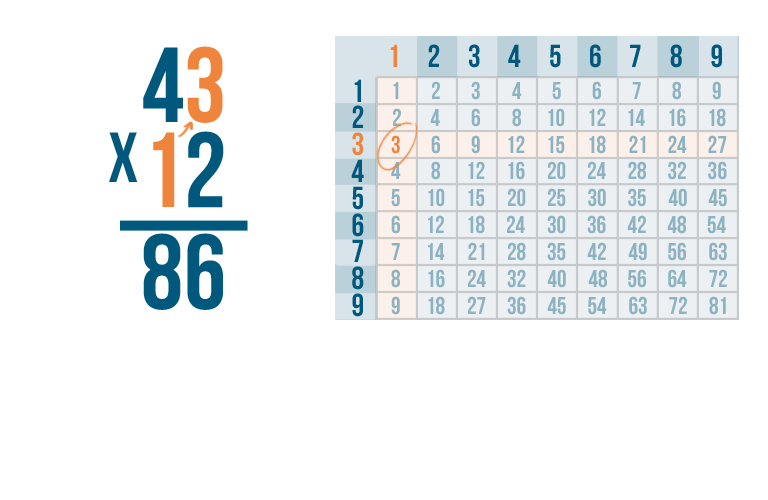
1 x 3 is 3...but we're not going to write 3 in the usual place.
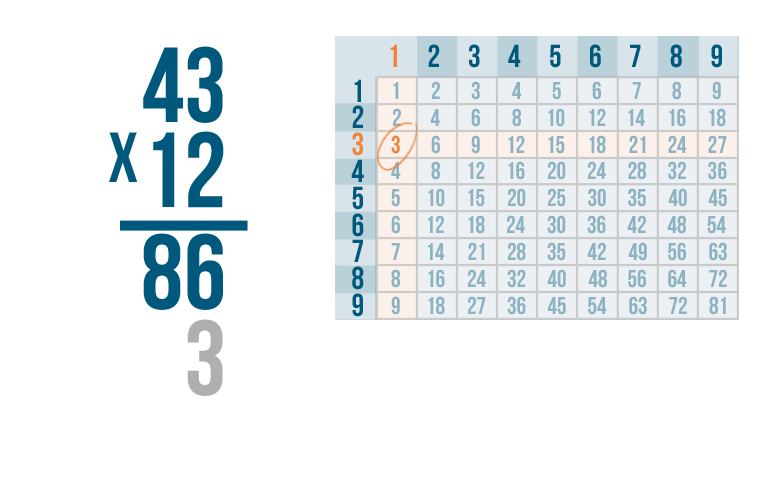
Instead of writing the 3 to the right, like we usually do...
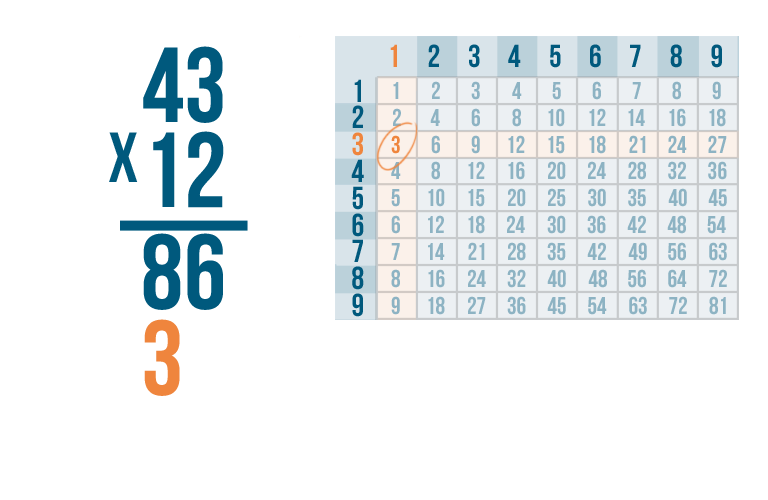
Instead of writing the 3 to the right, like we usually do... we're going to write it one place to the left, under the second set of digits.
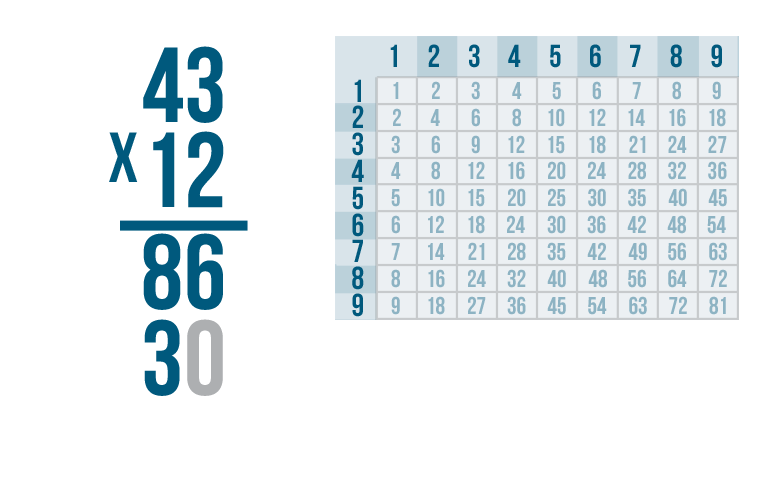
It's a good idea to mark the space you left blank. That way, you'll know not to accidentally write anything there. We'll add a 0, since zero is the same as nothing.
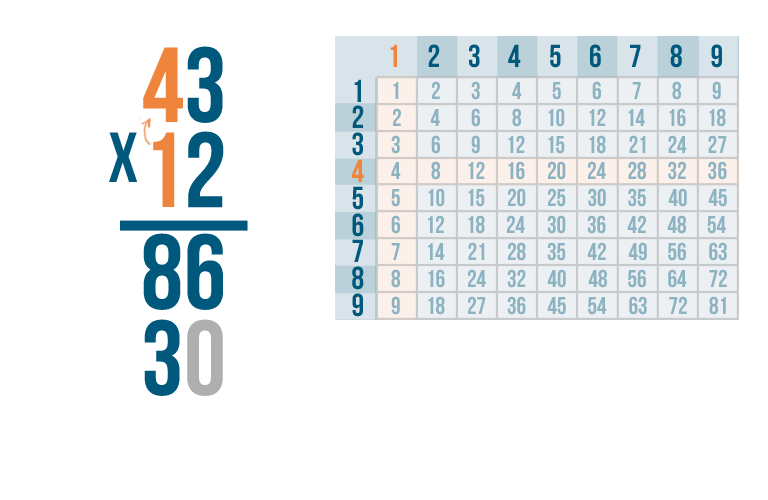
Now, let's multiply the last set of numbers. That's 1 x 4.
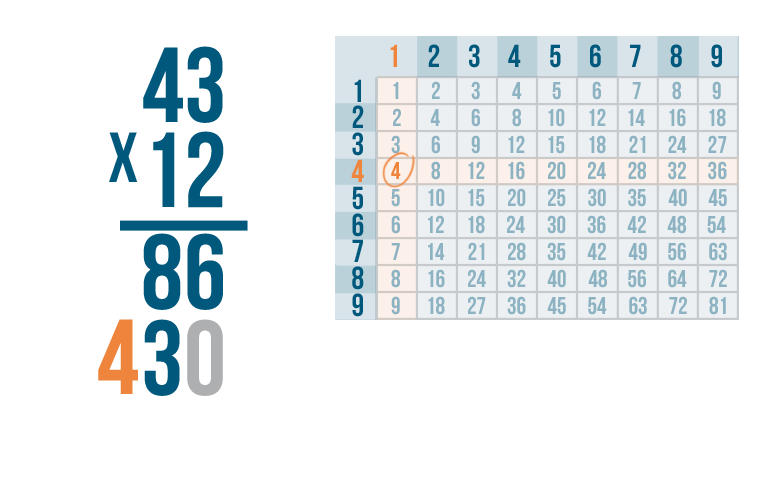
1 x 4 = 4. We'll write the 4 below the line, to the left of the 3 we just wrote.
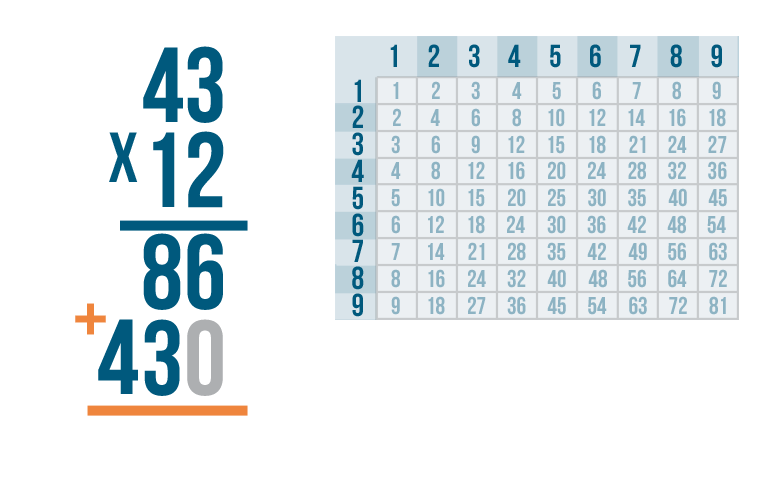
One last step. To get our final answer, we have to add the numbers we just got from multiplying.
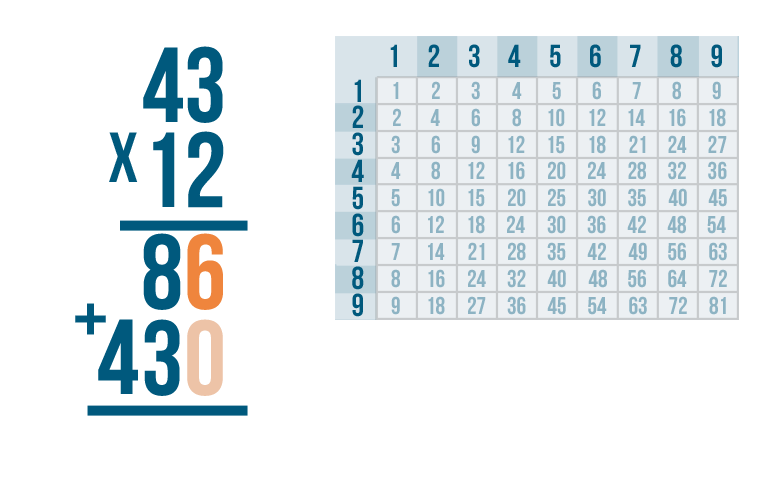
As always, we'll start adding from the right.
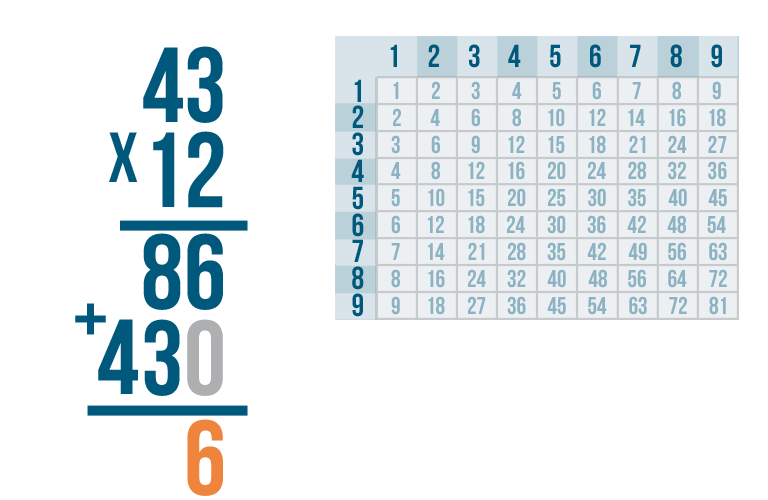
6 + 0 is 6. We'll write 6 below the line.
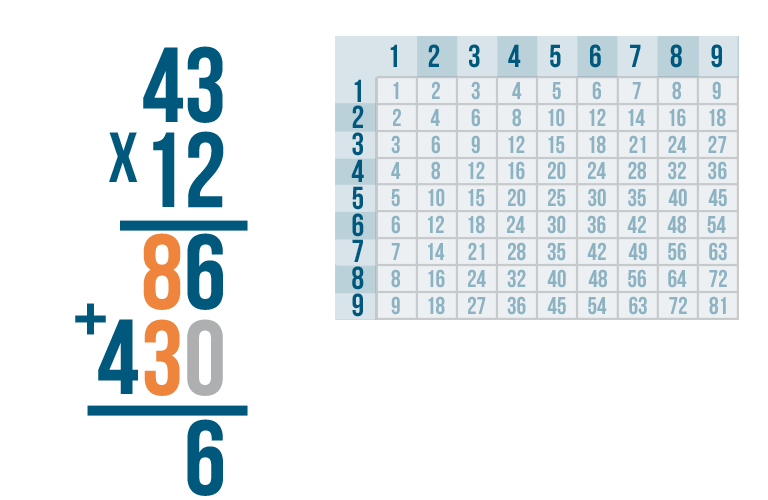
Next, 8 + 3.
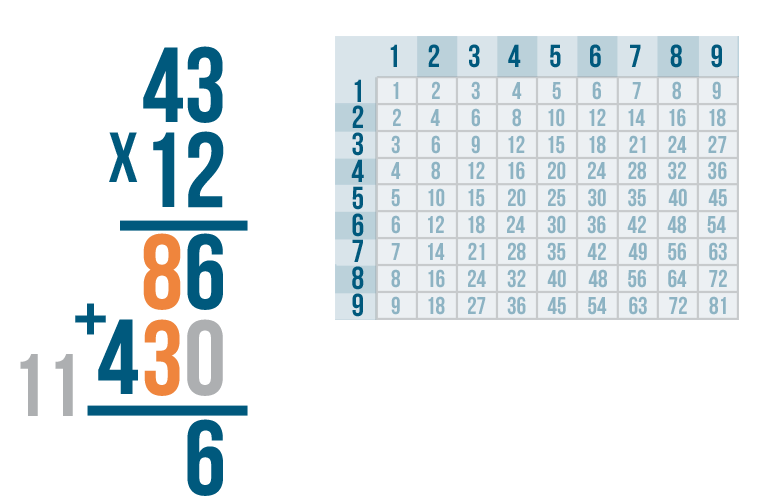
8 + 3 is 11. Since 11 is a 2-digit number, we'll have to carry.
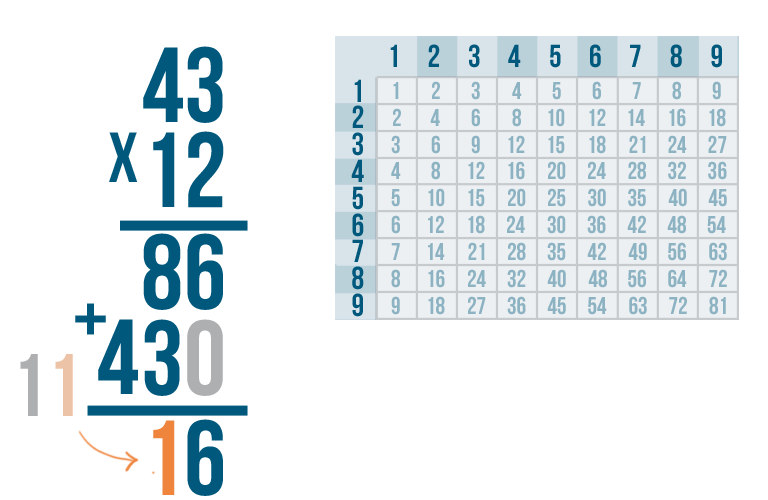
Write the right digit, 1, under the 8 and 3...

Write the left digit, 1, under the 8 and 3... then carry the right digit and place it above the digit to the left.
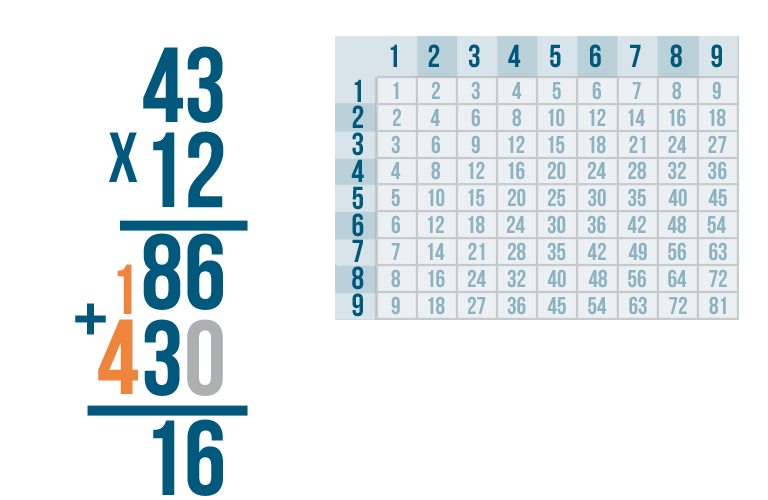
Finally, we'll add 4 to the 1 we just carried.
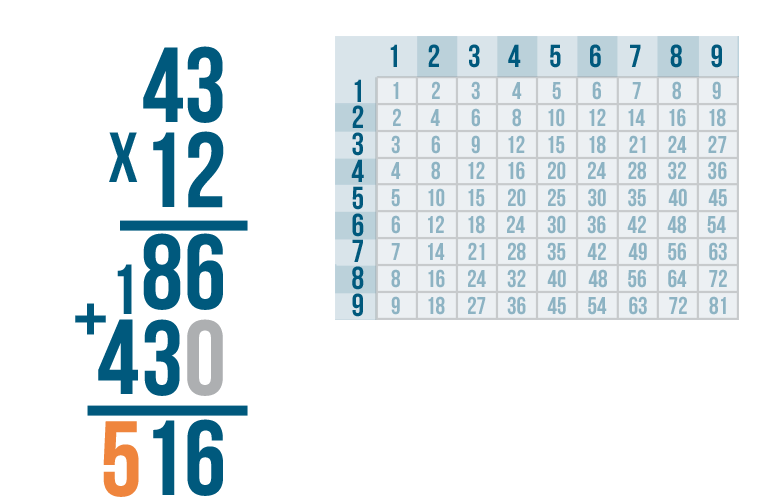
4 + 1 is 5.
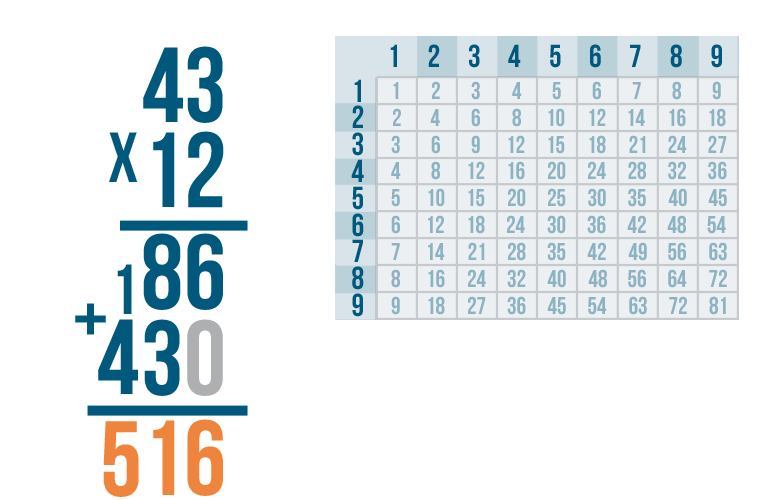
We're done! Our total is 516. In other words, 43 x 12 = 516.

Try this!
Stack and multiply these two-digit numbers. Then, check your answer by typing it in the box.
Multiplying two 3-digit numbers
Multiplying large numbers always works the same way, no matter how many digits the numbers have. When you're multiplying, be careful about writing the numbers in the correct places. Let's look at a problem with two 3-digit numbers to see how this works with even larger numbers.

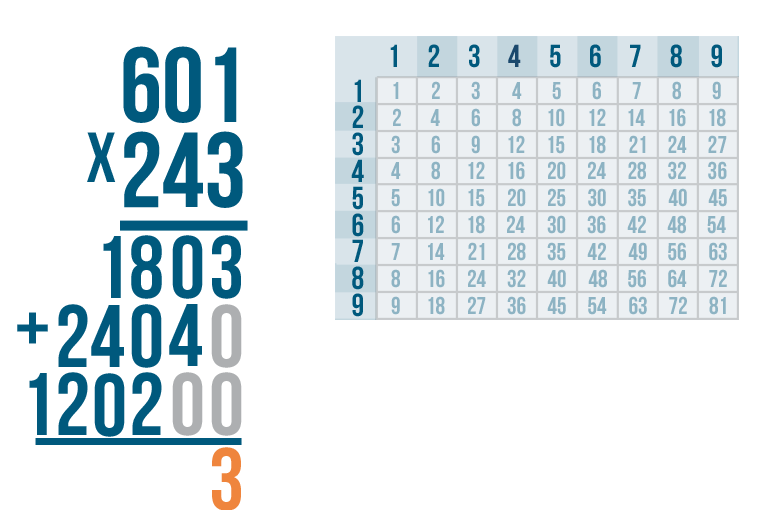
Let's try this problem: 601 x 243.

As always, start by multiplying the bottom-right digit by the top-right digit. So 3 x 1.
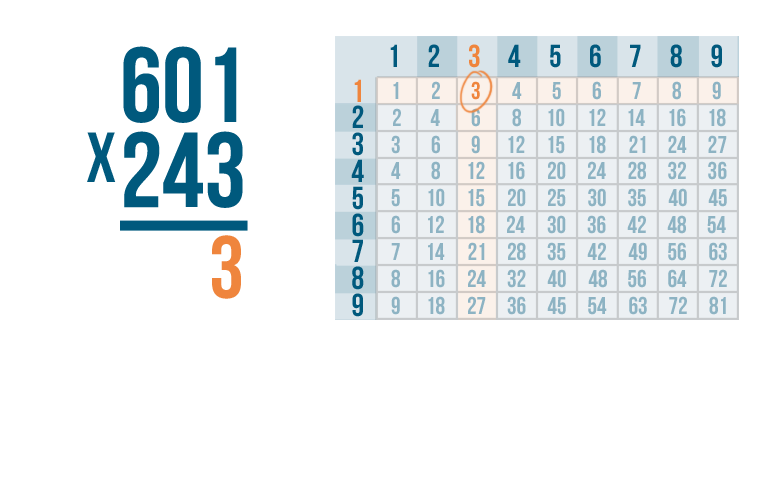
Thanks to our times table, we know that 3 x 1 is 3. Write the 3 underneath the line, to the far right.
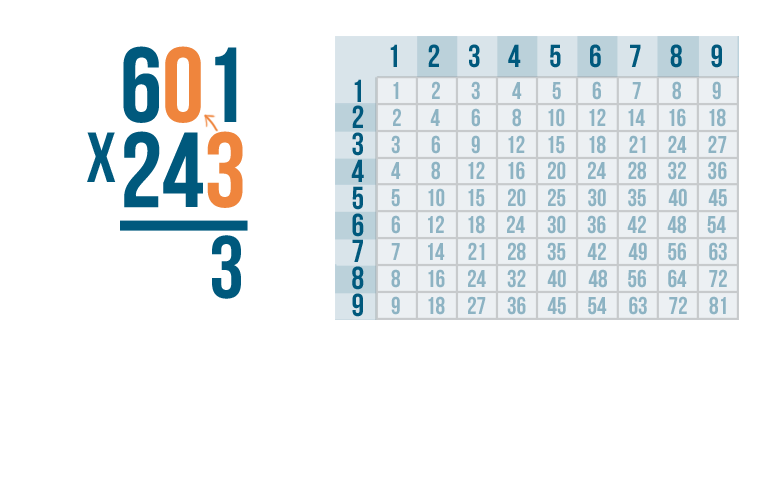
Now multiply 3 by the next number, 0.
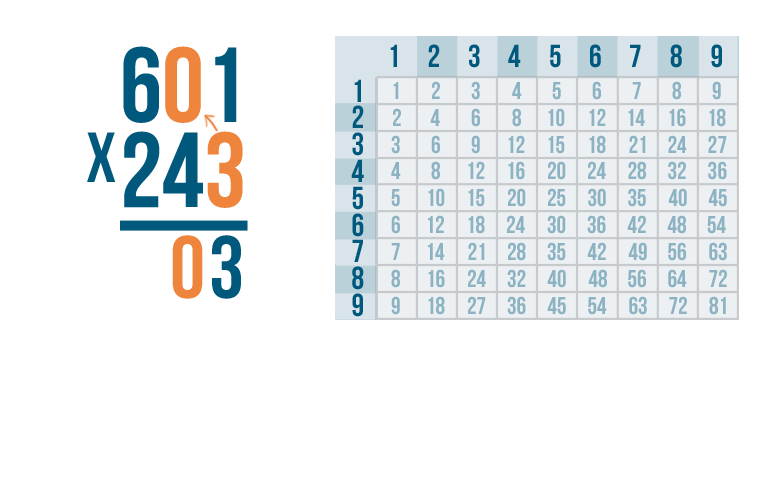
Anything times zero is 0, so write 0 underneath the line, next to the 3.
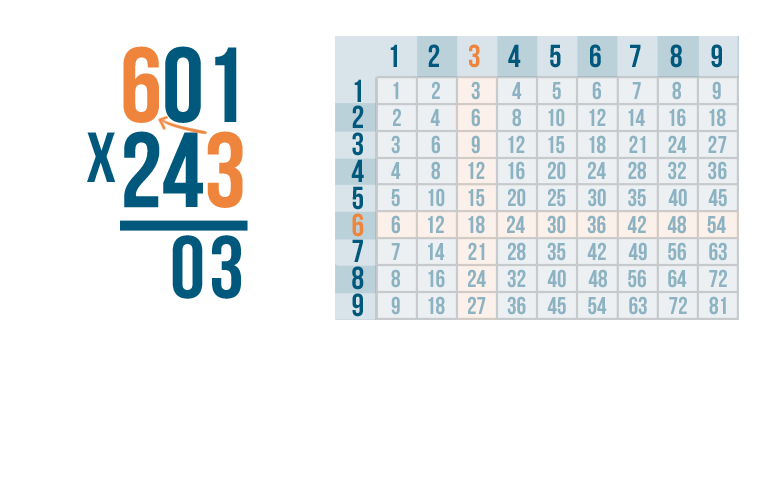
Next, 3 x 6.
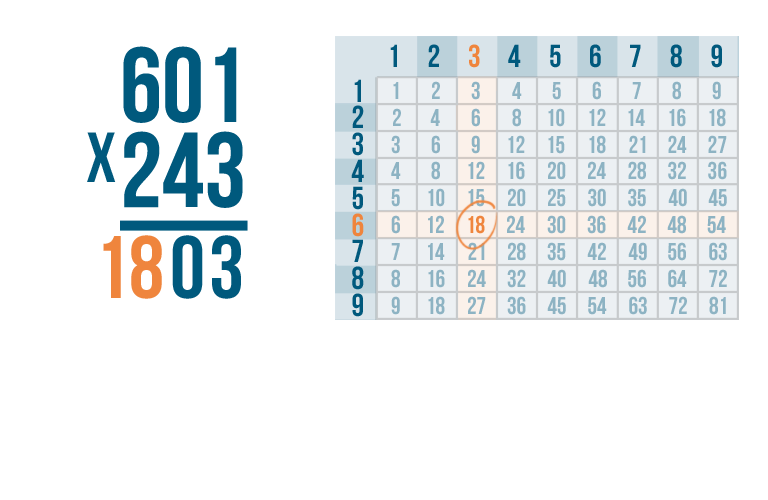
3 x 6 = 18. Write 18 beneath the line.

We're done with the first digit in the bottom number.

Next, multiply by the second number on the bottom, 4.
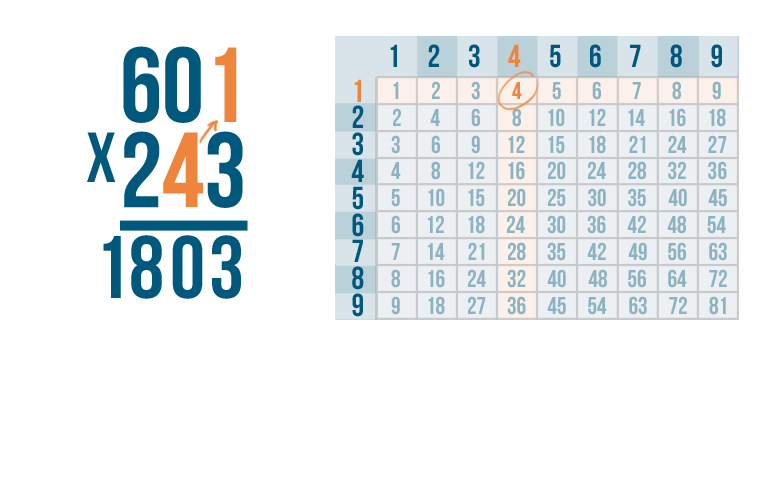
4 x 1 is 4. Remember, you're not going to write the 4 all the way to the right.
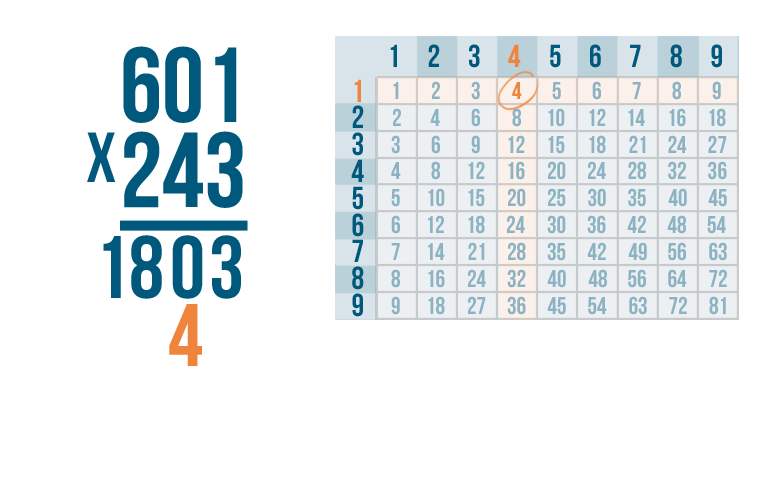
Instead, write the 4 one place to the left, underneath the second set of numbers.
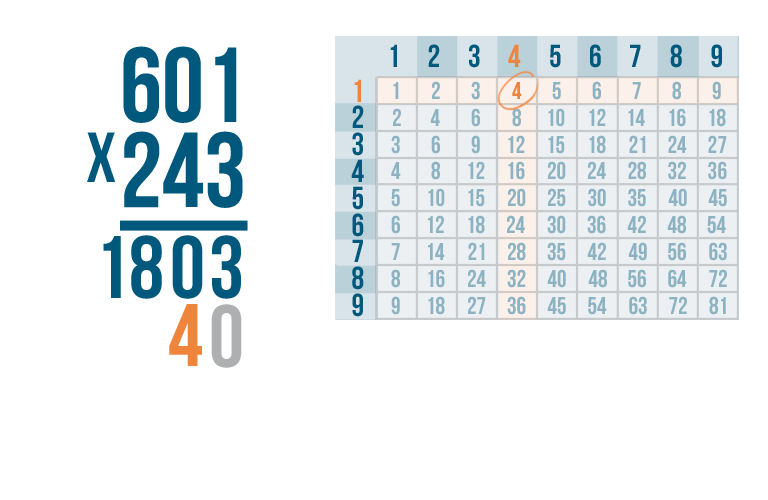
In order to help keep everything aligned, we'll put a zero as a placeholder on the right of the four.

Now, let's move on to the next number on top — 0.

4 x 0 is 0. Write the 0 underneath the line.
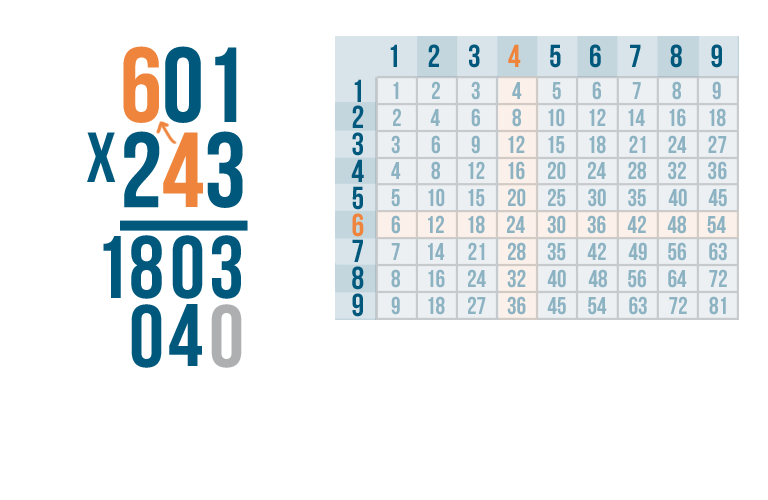
Next, multiply the 4 by the final digit in the top number — 6.
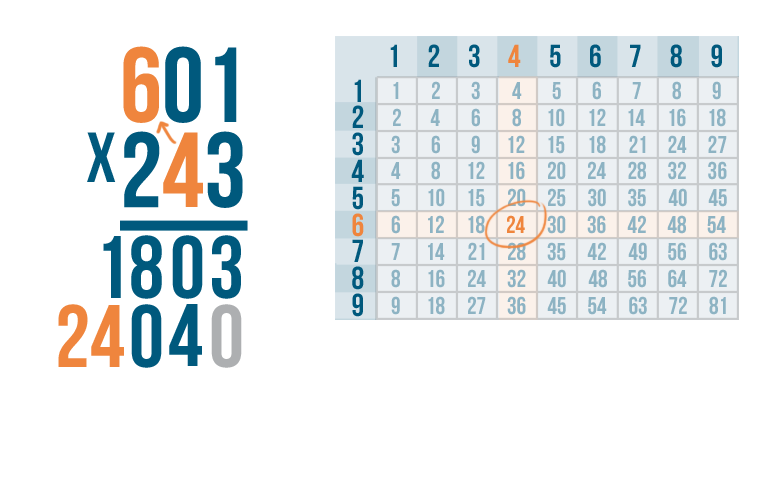
4 x 6 is 24. Write 24 underneath the line.

We're ready to multiply by the final digit in our bottom number — 2.
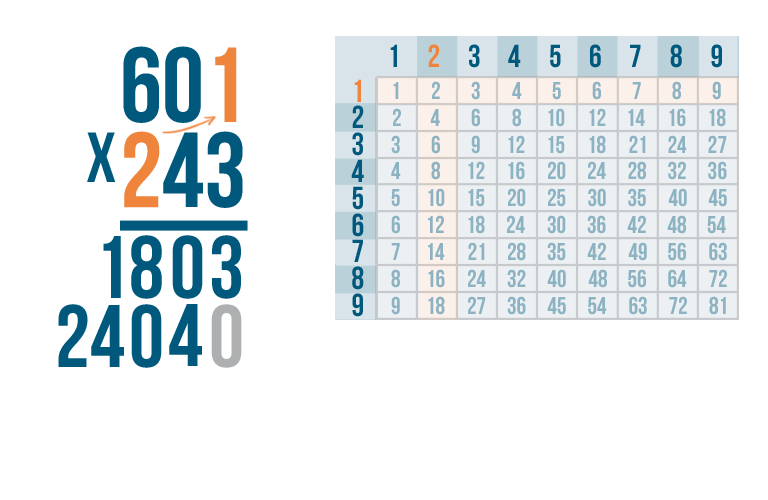
As always, start with the top right digit,1.
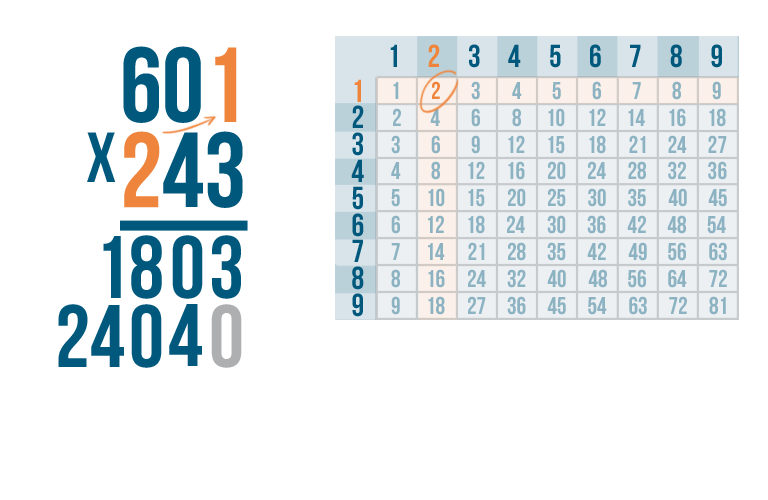
2 x 1 is 2.
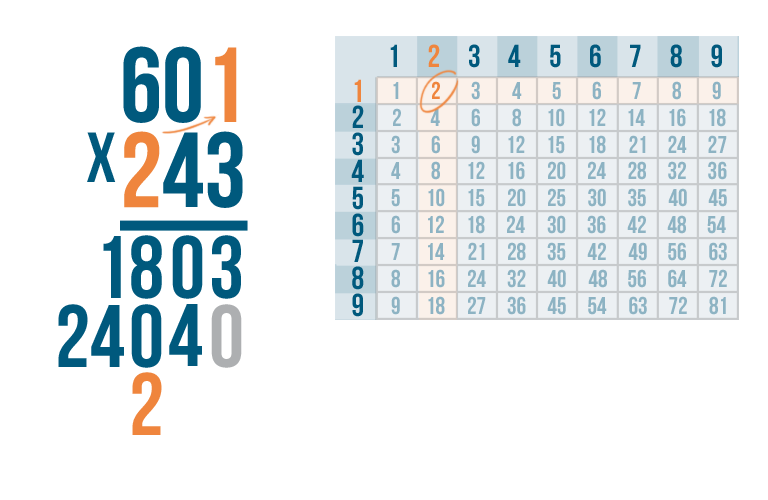
We'll write 2 beneath the line, two spaces over from the right.
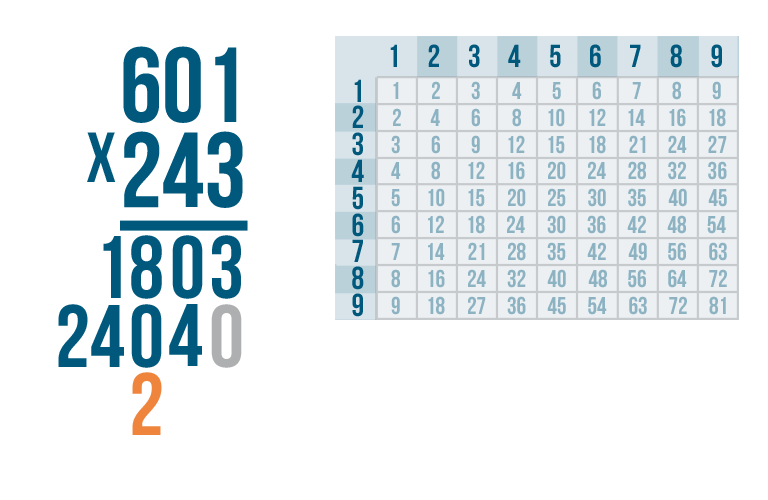
Notice where we put the 2.
When we multiplied with the first digit in the bottom number...
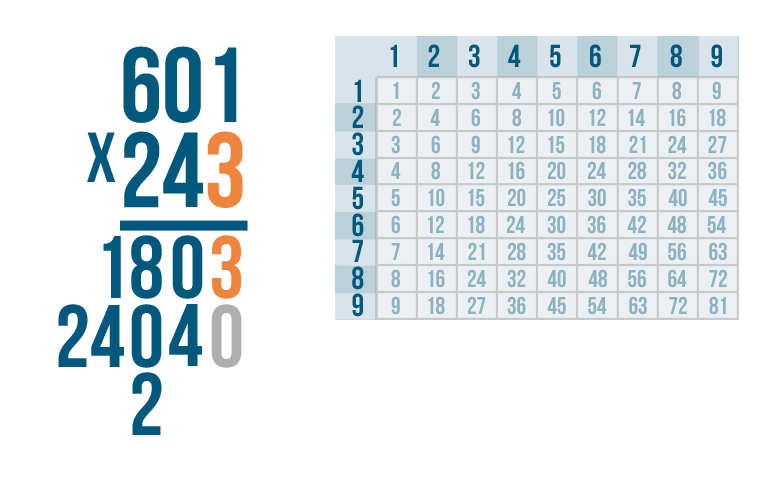
When we multiplied with the first digit in the bottom number... we lined up the product all the way to the right.

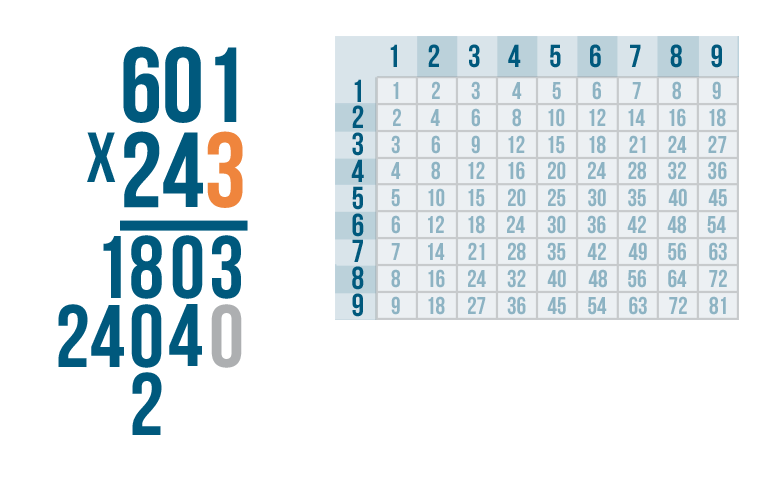
When we multiplied with the second digit...
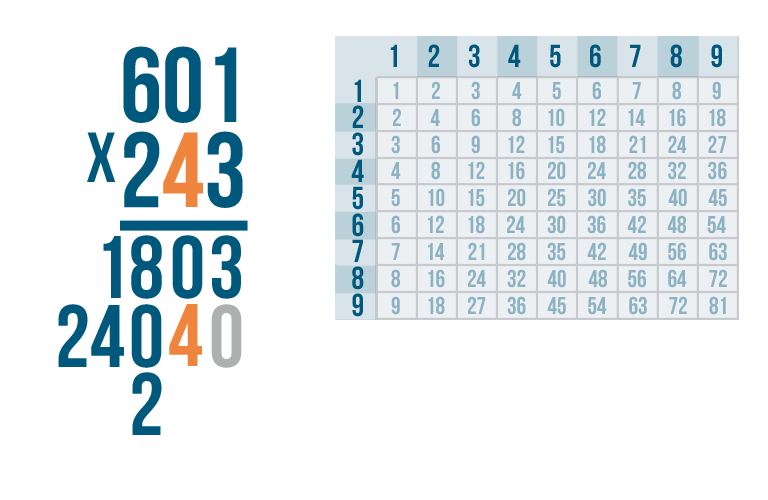
When we multiplied with the second digit... we wrote the product one space to the left.
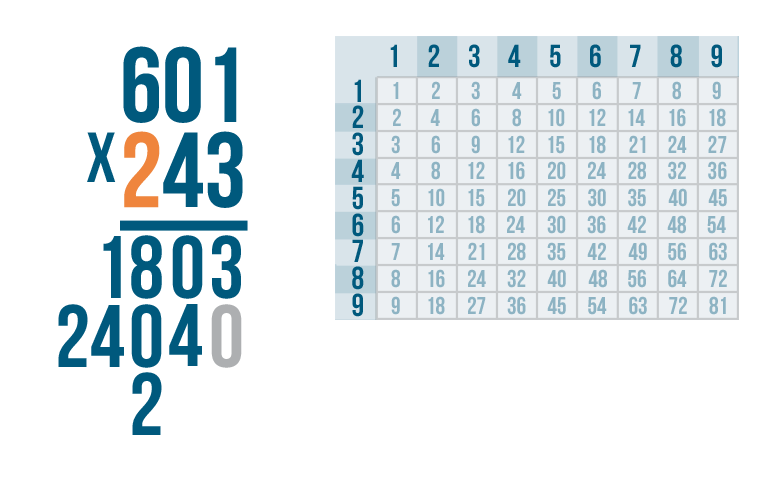
Now that we multiplied with the third digit...

Now that we multiplied with the third digit...we placed the product two spaces to the left.


You might have noticed a pattern. Each time we multiplied with a new digit, we wrote the product one digit further to the left. This is true no matter how many digits are in the numbers you're multiplying with.

Let's get back to our problem. We just multiplied 2 x 1.

The next digit is 0.

2 x 0 is 0. Write 0 underneath the line.
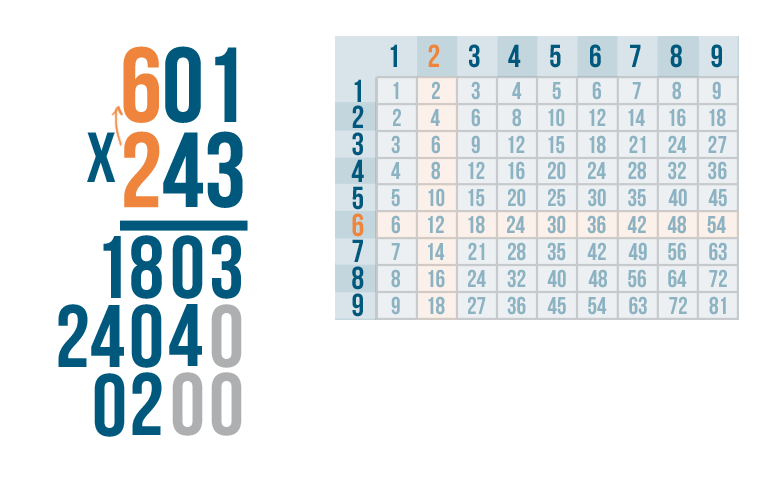
Finally, multiply 2 x 6.
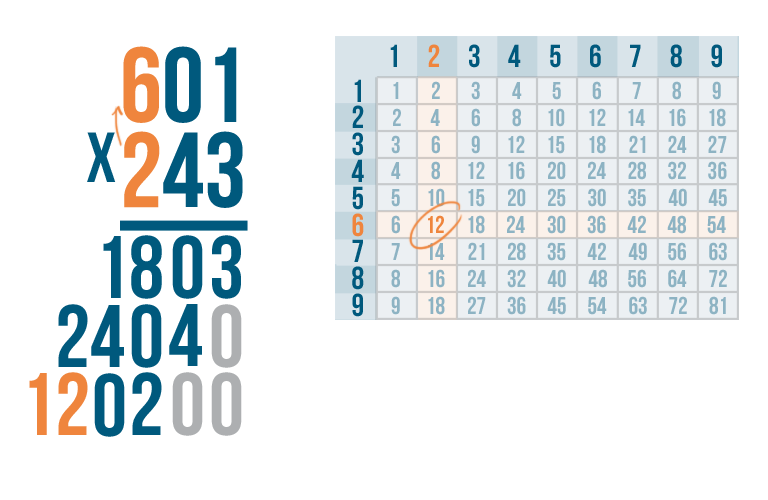
2 x 6 is 12. Write 12 below the line.

Time to add. As always, start with the digits on the far right. Here, that means we're adding 3 + 0 + 0.
3 + 0 + 0 = 3. Write 3 directly under the digits we just added.
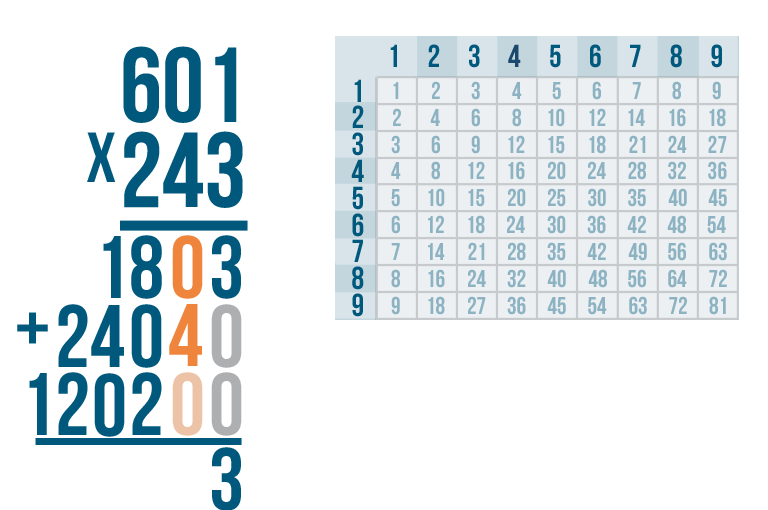
Next, we'll add 0 + 4 + 0.

0 + 4 + 0 is 4.

Now, the next set of digits, 8 + 0 + 2.

8 + 0 + 2 = 10. 10 is a two-digit number, so we'll have to carry. Write the 0 beneath the digits we just added, and place the 1 above the next set of digits.

It's time to add the 1 we just carried. That means we're solving for 1 + 1+ 4 + 0.

1 + 1 + 4 + 0 = 6. Write 6 below the line.

Next, 2 + 2.

2 + 2 = 4. Write 4 beneath the line.

There's only one digit to the left — 1.

One plus nothing is 1, so we'll write 1 below the line.

We're finally done! Our total is 146,043, or one hundred forty-six thousand and forty-three. 601 x 243 = 146,043.

What a huge number! If that problem seemed complicated, don't worry. You'll rarely need to multiply such large numbers. When you do, you can always use a calculator. Still, it's good to know how. If you can multiply these problems, you can multiply anything.
Practice!
Practice multiplying large numbers. Then check your answer by typing it in the box.
Set 1
Set 2
Set 3
/en/multiplicationdivision/video-multiplication/content/