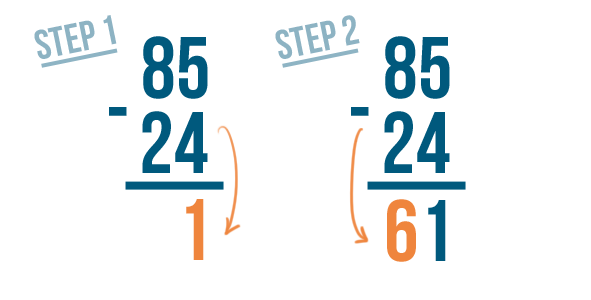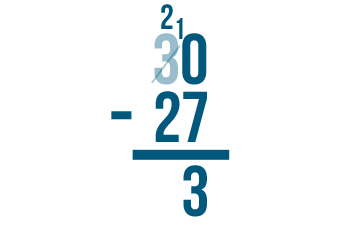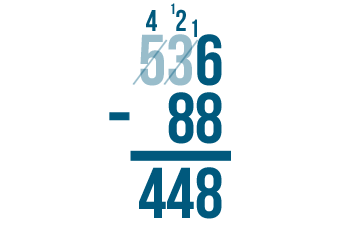Lesson 5: Subtracting Two- and Three-Digit Numbers
/en/additionsubtraction/introduction-to-subtraction/content/
Subtracting larger numbers
In Introduction to Subtraction, we learned that counting and using visuals can be useful for solving basic subtraction problems. For instance, say you have 9 apples and you use 6 to make a pie. To find out how many apples are left, you could represent the situation like this:
It's easy to count and see that 3 apples are left.
What if you need to solve a subtraction problem that starts with a large number? For instance, let's say instead of making an apple pie, you want to pick apples from an apple tree. The tree has 30 apples and you pick 21. We could write this as 30 - 21.
You might see why counting to solve this problem isn't a good idea. When you have a subtraction problem that starts with a large number, it could take a long time to set up the problem. Imagine the time it would take to count out 30 objects and then take away 21! Also, it would be easy to lose track as you counted. You could end up with the wrong answer.
For this reason, when people solve a subtraction problem with large numbers, they set up the problem in a way that makes it easy to solve one step at a time. Let's see how this works with another problem: 79 - 13.
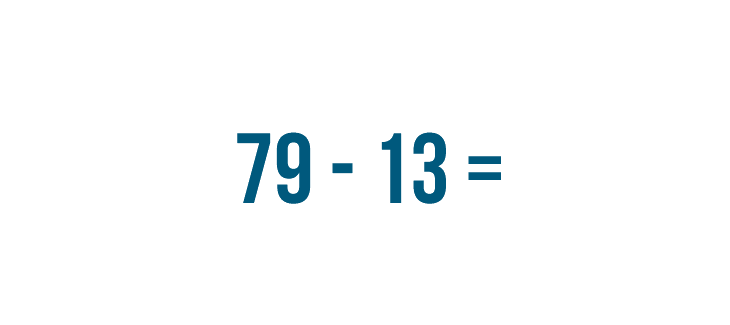
In the last lesson, we learned how to write expressions. However, subtracting with larger numbers is easier when the expressions are written in a different way.
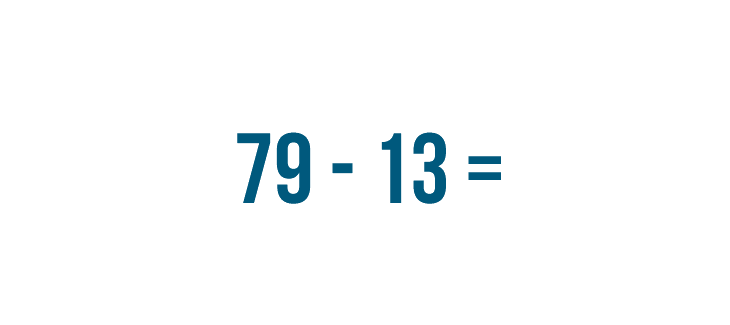
Instead of writing the numbers side by side…
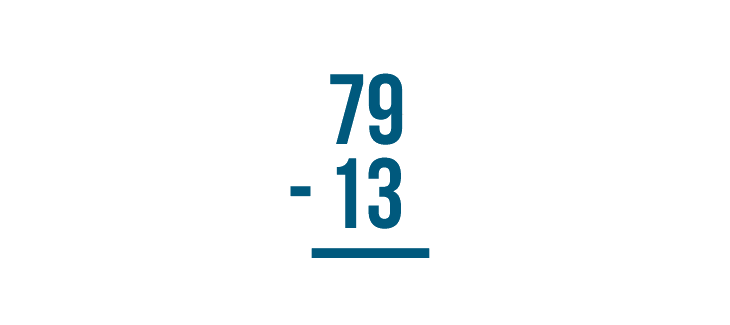
Place the numbers so they are stacked — one number on top and one number on the bottom.
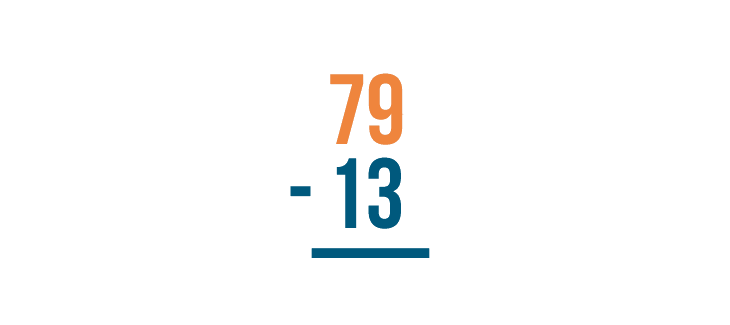
With a stacked subtraction expression, the larger number is always written on top. Here, that number is 79.
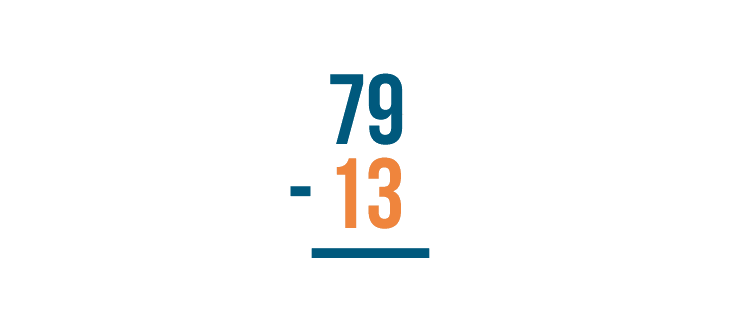
Write the amount being subtracted underneath the top number. That's 13.

Put the minus sign to the left of the numbers.
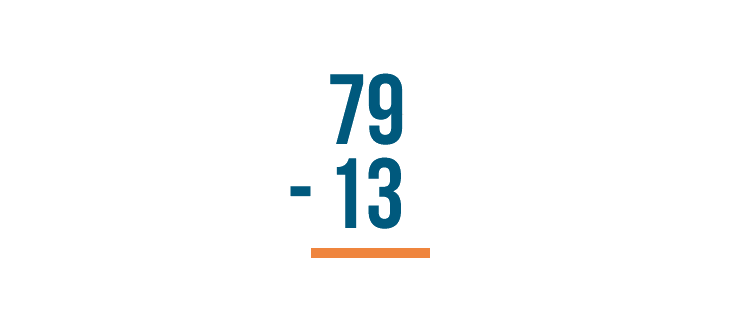
Instead of an equals sign, put a line underneath the bottom number.
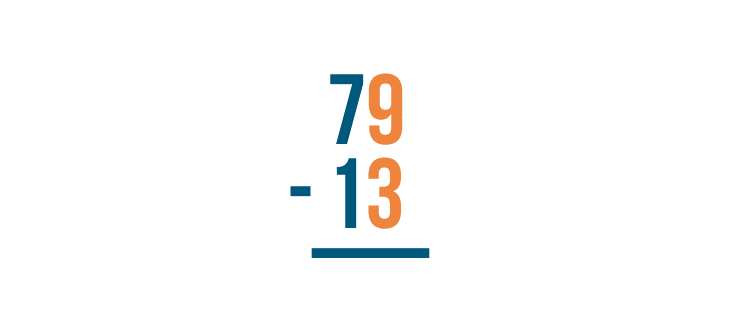
When you stack a subtraction expression, make sure the numbers are lined up correctly. They are always lined up on the right. Here, we lined up 9 and 3.

Here's another problem, 576 - 2. With this problem, see how we lined up the numbers to the right?
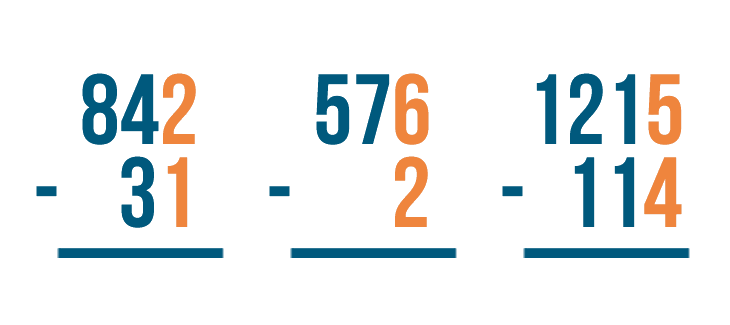
No matter how many digits are in the numbers, always line up the numbers to the right.

We can see that 79 - 13 and 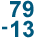 mean the same thing — they're just written differently.
mean the same thing — they're just written differently.
Solving Stacked Subtraction Problems
If you feel comfortable with the subtraction skills from Introduction to Subtraction, you're ready to start solving stacked subtraction problems.
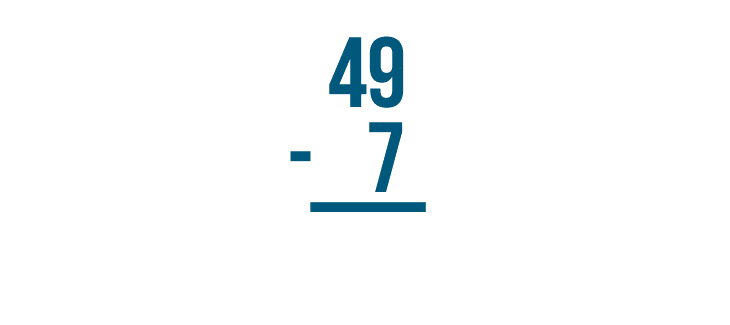
Let's try to solve 49 - 7.
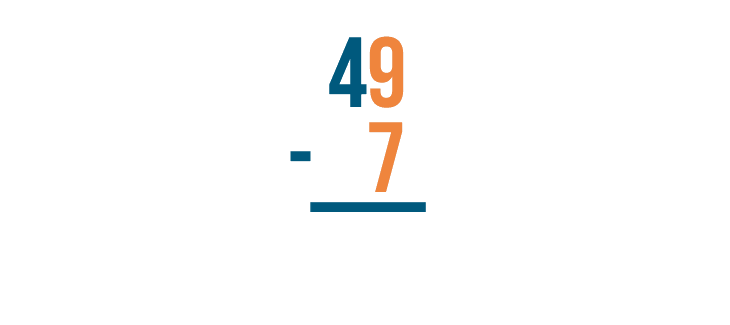
With all stacked subtraction problems, we start with the digits that are farthest to the right. Here, we'll begin with 9 and 7.
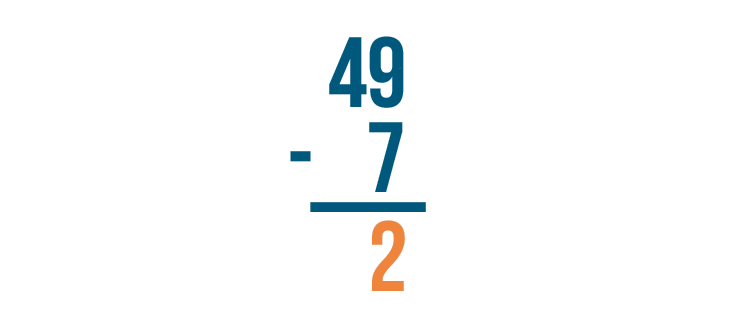
9 - 7 = 2. The difference is 2. It's important to write 2 directly beneath the digits we just subtracted.
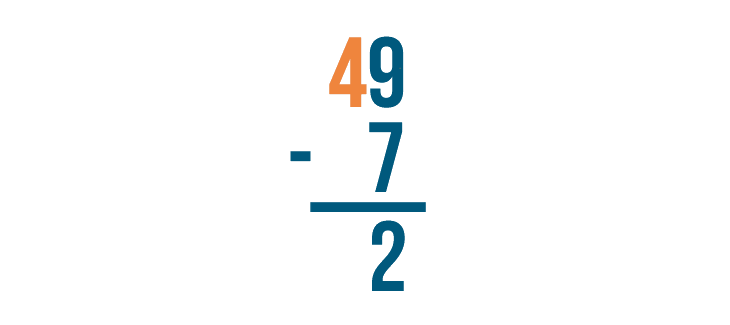
Now let's find the difference of the digits to the left. The top digit is 4, but there's nothing beneath it.
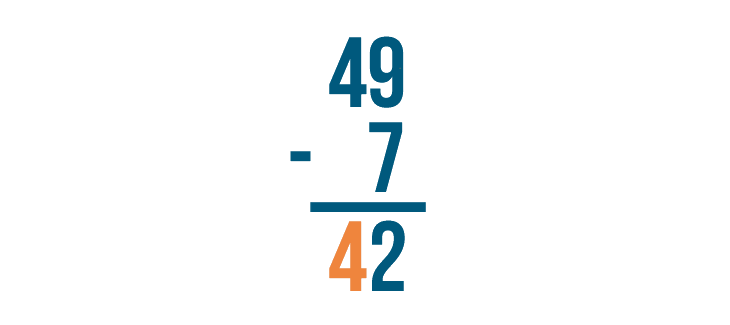
4 minus nothing is 4, so we'll write 4 beneath the line.
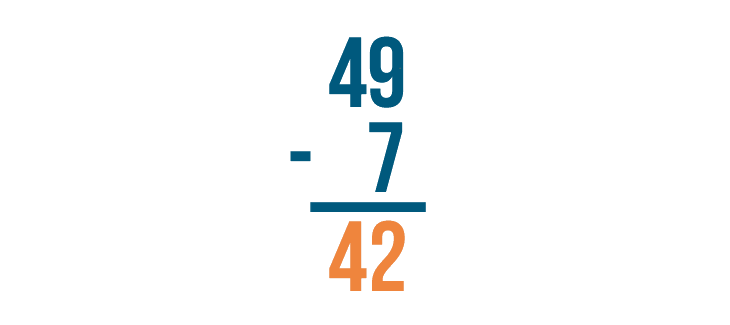
Our result is 42. 49 - 7 = 42.

Let's see how this works with another problem: 88 - 62.
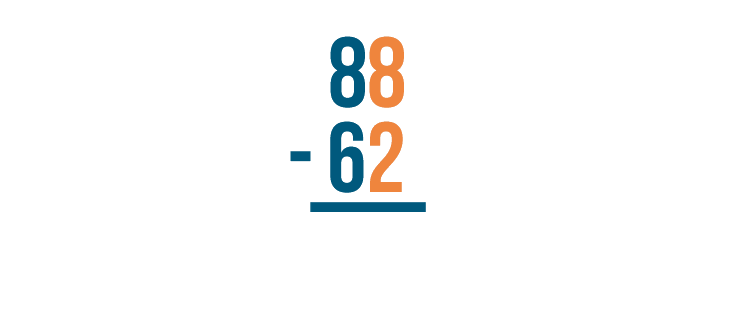
As always, start with the digits that are farthest to the right. Here, they are 8 and 2.
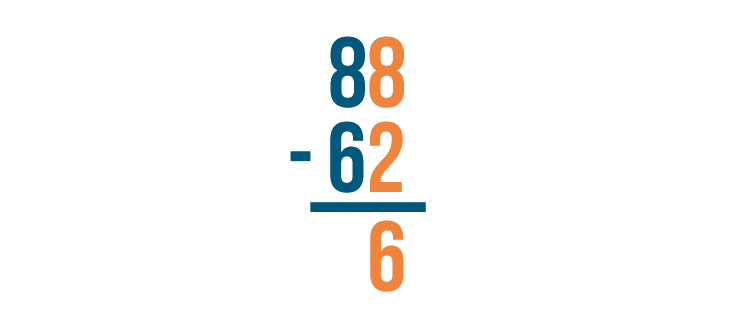
8 - 2 = 6. Make sure to write 6 below the line.
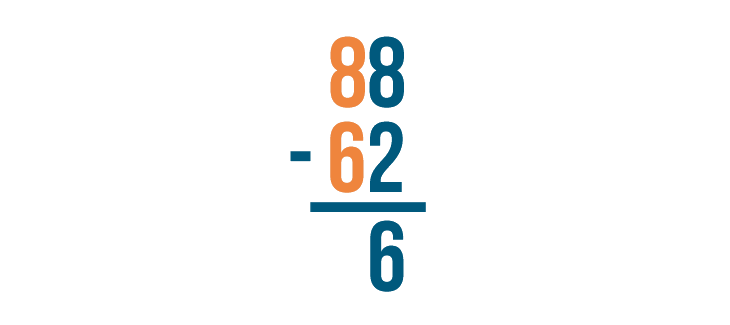
Next, find the difference of the digits to the left, 8 and 6.
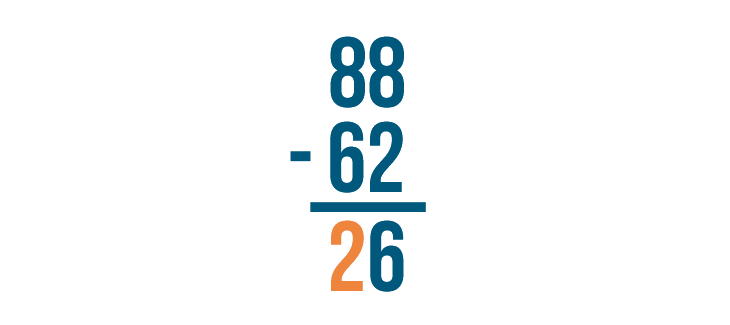
8 - 6 is 2. Write 2 below the line.

The answer is 26. 88 - 62 = 26.

In the slideshow, you saw that stacked subtraction problems are always solved from right to left. The expressions below are solved the same way. First, the bottom right digit is subtracted from the top right digit. Then, the bottom left digit is subtracted from the top left digit.
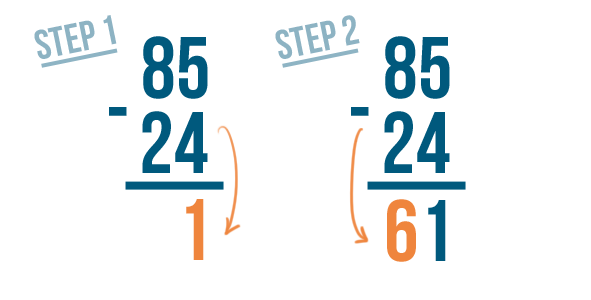
Try This!
Stack these subtraction problems and solve them. Then, check your answer by typing it into the box.
Subtracting Larger Numbers
Stacked subtraction can also be used for finding the difference of larger numbers. No matter how many digits there are, you subtract the same way every time — from right to left.
Try This!
These subtraction problems have larger numbers. Solve them, and then check your answer by typing it into the box.
Borrowing
Sometimes when you subtract, you will notice that the top digit is smaller than the bottom. For example, take a look at this problem:
Normally, we'd start on the right with 5 - 9. However, since 9 is bigger than 5, we can't subtract normally. Instead, we have to use a technique called borrowing.
Let's see how it works.

First, we'll make sure the expression is set up correctly. The larger number is stacked on top of the smaller number.
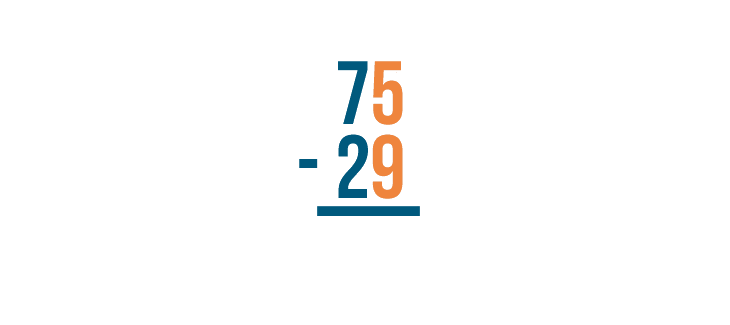
As with all stacked subtraction problems, begin with the digits farthest to the right. Here, they are 5 and 9.
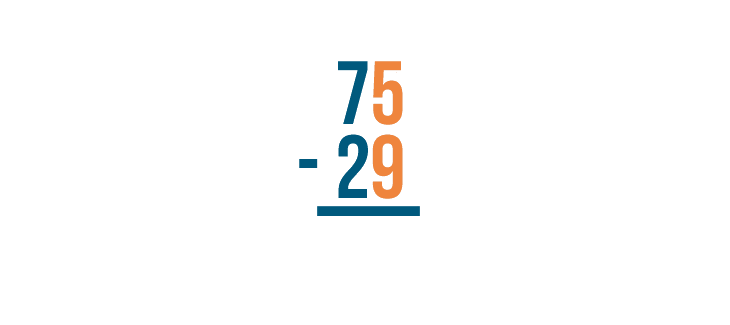
5 is smaller than 9, so we'll need to borrow to make 5 larger.
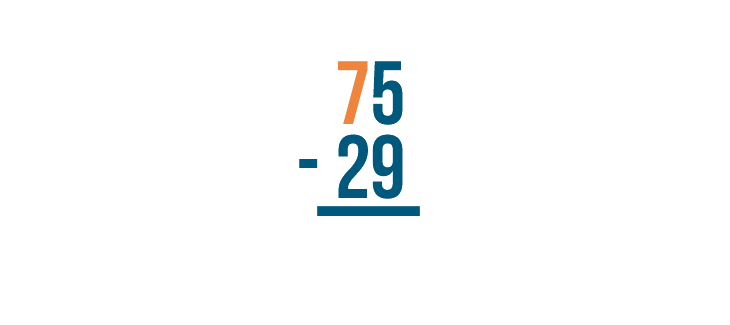
We'll borrow from the digit to the left of 5. Here, it's 7. We'll take 1 from it....
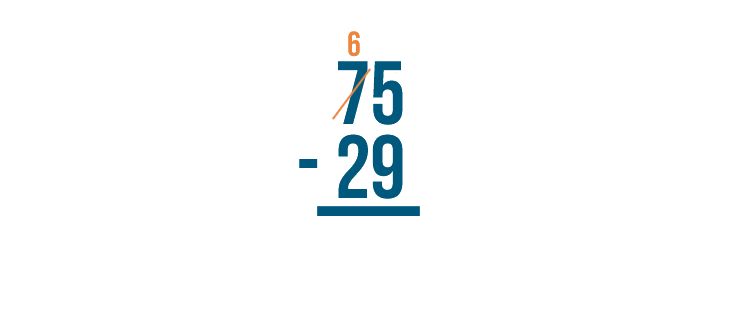
7 - 1 = 6. To help us remember that we subtracted 1, we'll cross out the 7 and write 6 above it.

Then, we'll place the 1 we took next to the 5...
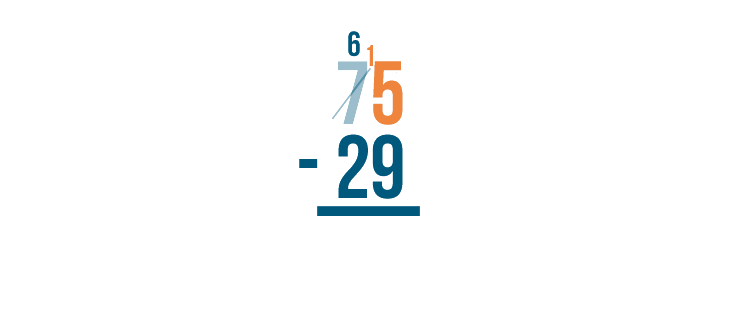
5 becomes 15. See how it looks like 15?
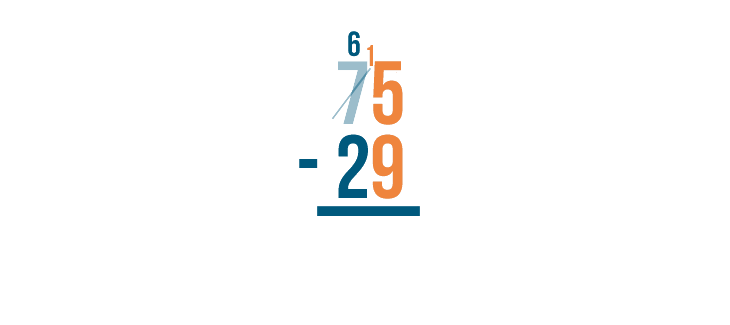
15 is larger than 9, which means we can subtract. We'll solve for 15 - 9.
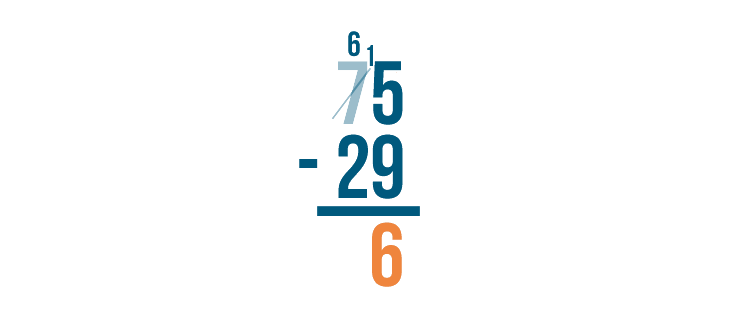
15 - 9 = 6. We'll write 6 beneath the line.
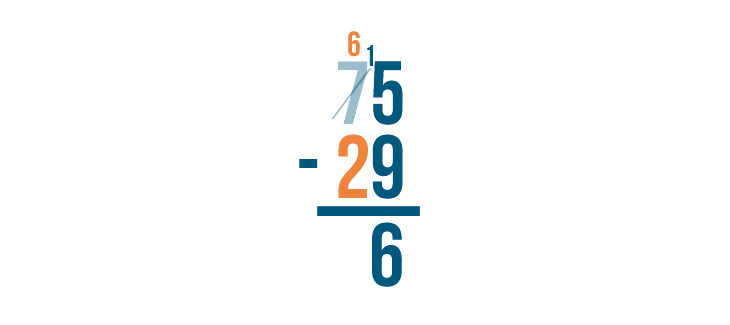
Next, find the difference of the digits to the left: 6 - 2.
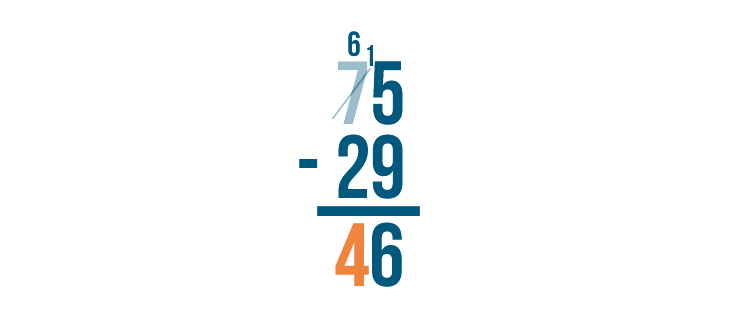
6 - 2 = 4. We'll write 4 beneath the line.
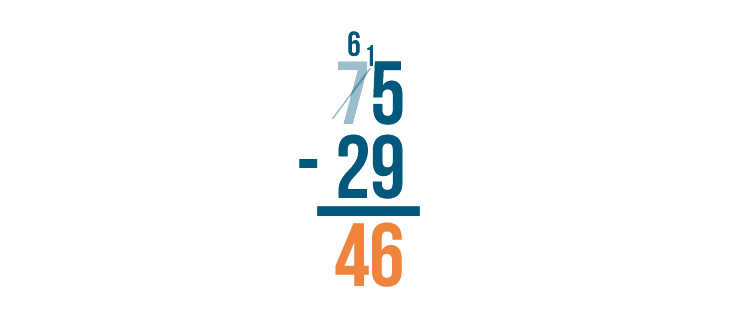
Our answer is 46. 75 - 29 = 46.

As you borrow, always cross out the digit you borrow from and write the new value above it. Remember to always place the 1 next to the smaller digit.
Try This!
Try these problems to practice borrowing. Check your answer by typing it into the box.
Borrowing More Than Once
Sometimes the top number might have two or more digits that are smaller than the digits beneath them. In that case, you'll need to borrow more than once. It will always work the same way. You'll always subtract 1 from the digit to the left and place 1 next to the smaller digit.
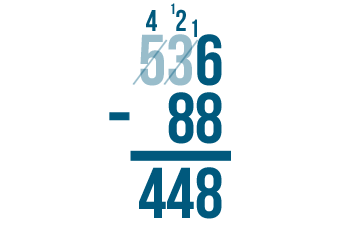
In some cases, you might notice that the number to the left is zero. Check out the slideshow below to see an example of what to do.
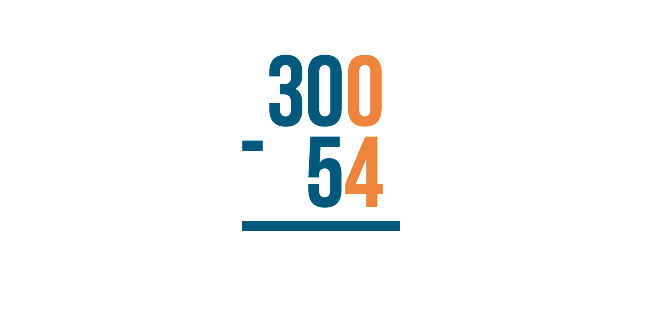
Let's look at the example 300 minus 54. We would begin on the right with 0 minus 4. However, zero is smaller than 4, so we would need to borrow from the next digit to the left.
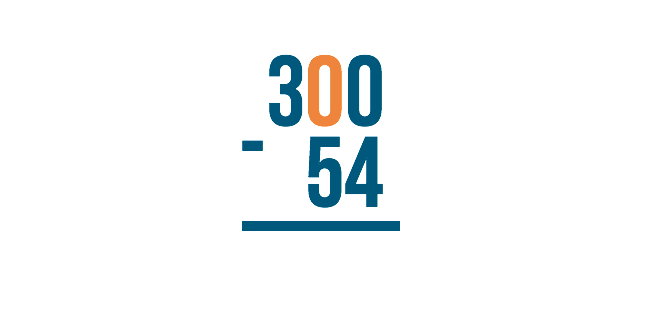
The next digit to the left, however, is zero! We can't borrow if nothing is there. So what do we do?
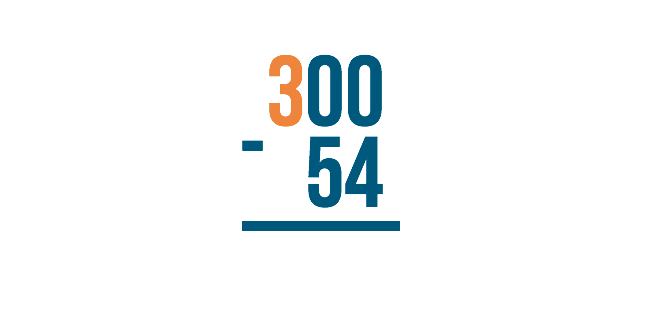
We have to go to the next digit to the left. Think of it like asking your neighbor for a cup of sugar. If the first neighbor doesn't have any, you would move to the next neighbor over to ask for some to borrow.
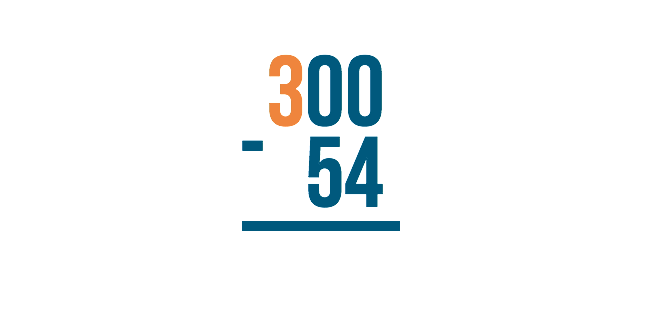
Since the next number over is 3, we'll borrow from that.
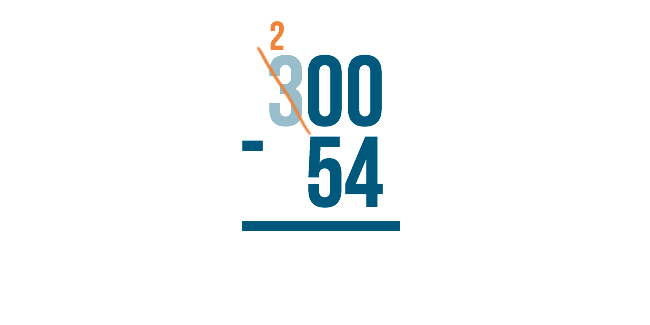
Just like when we borrow normally, we'll subtract 1 from 3 to make it 2. We'll place the 1 next to the number on the right to make it 10.

Just like when we borrow normally, we'll subtract 1 from 3 to make it 2. We'll place the 1 next to the number on the right to make it 10.

Remember though, we originally needed to borrow in order to do 0 minus 4. Now that we have 10 in the middle, we can borrow from it.
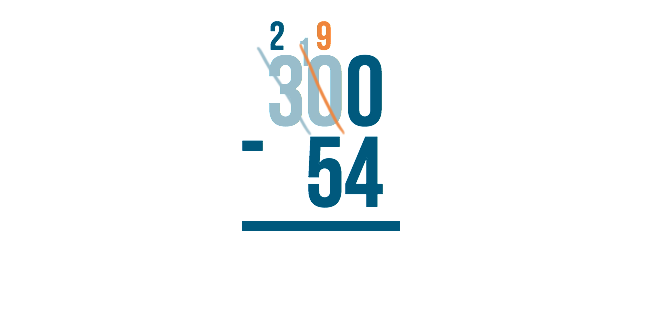
Cross out the 10 and subtract 1 to make it 9.

Then, place the 1 next to the 0 in order to make it 10. Now you're ready to subtract.
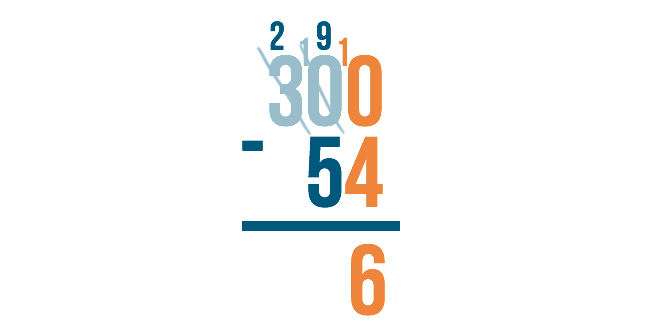
10 minus 4 is 6.
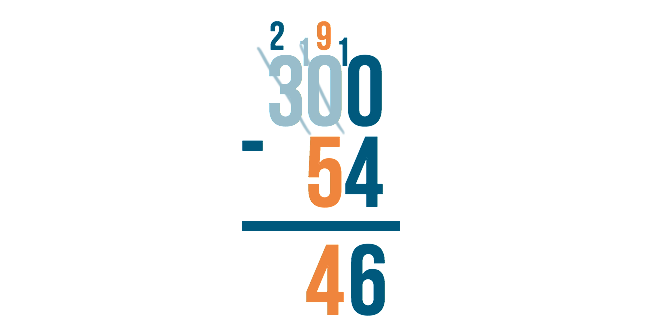
9 minus 5 is 4.
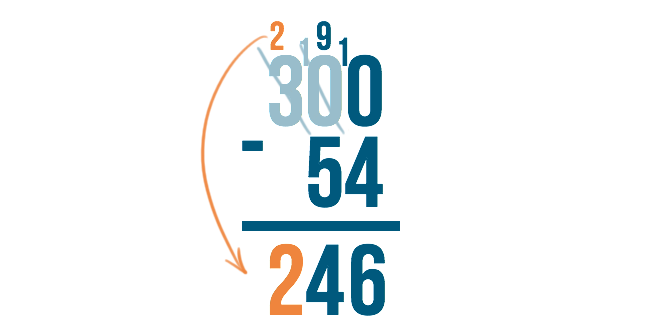
There is nothing to subtract from the 2, so we just bring it down, and we're finished!
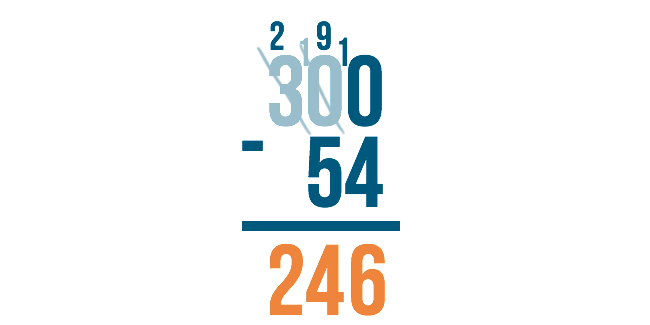
The answer is 246.

Try This!
Try solving these subtraction problems to practice borrowing more than one time. Check your answer by typing it in the box.
Checking Your Work
In the last few lessons, you learned how to solve addition and subtraction problems. As you practice these math skills, it's a good idea to get into the habit of checking your work. Checking will help you know if your answers are correct. When you're ready to check the answer to subtraction problems, you'll need to use addition.
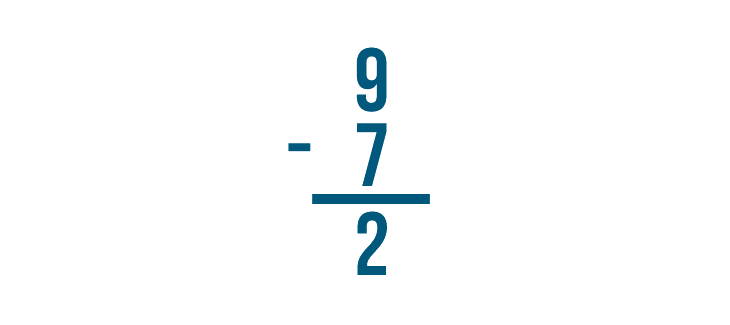
Let's look at this problem: 9 - 7 = 2.
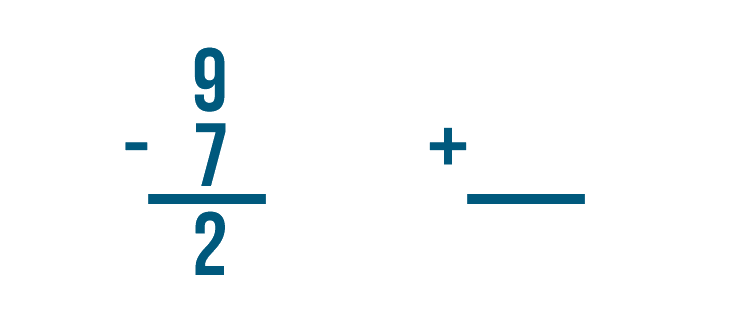
How do we know that 2 is the correct answer? We can check by adding.
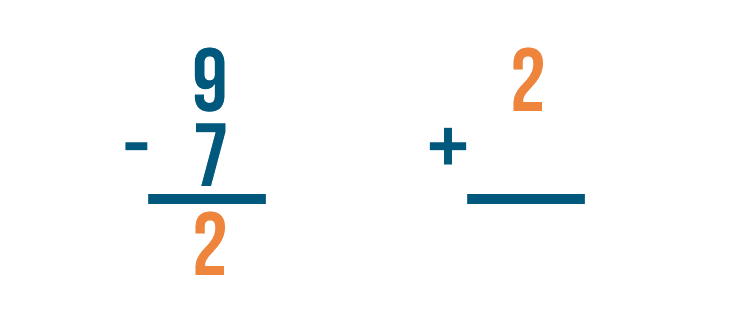
Let's set up our addition problem. First, we'll write the subtraction problem's answer. That means we'll write 2.
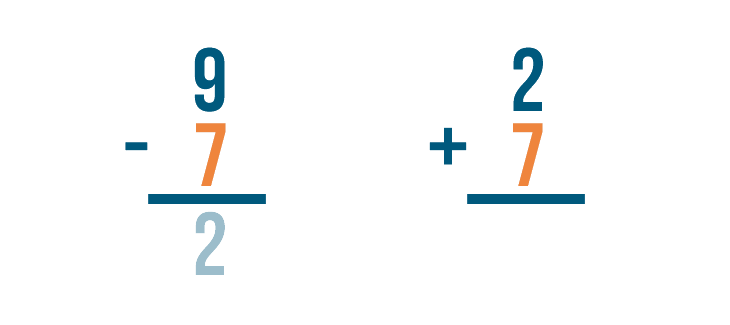
Next, we'll add the amount that was subtracted, 7.
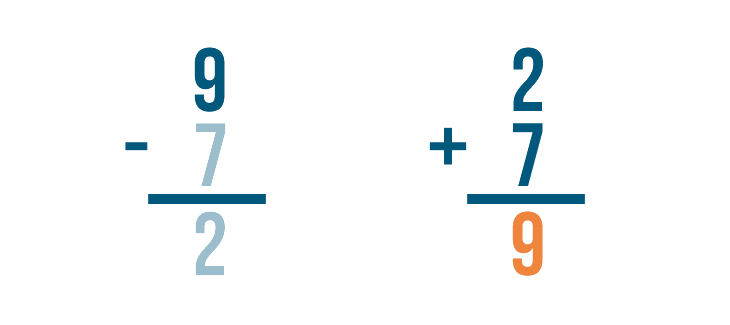
Time to add. 2 + 7 = 9.
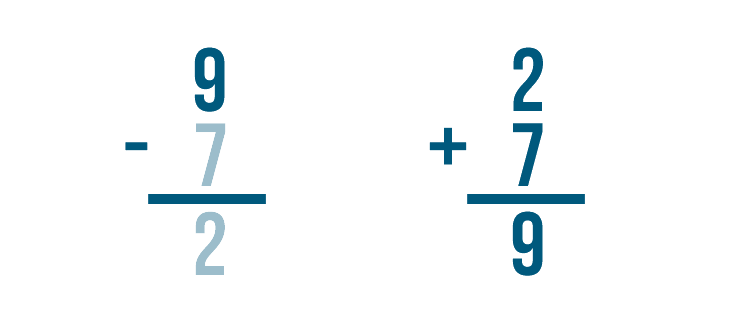
If we subtracted correctly, the answer will match the larger number in our subtraction problem.
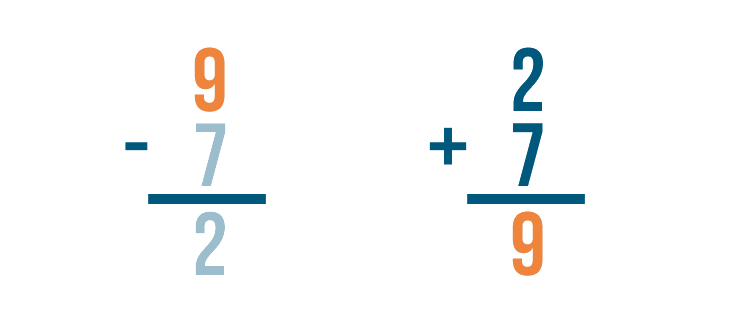
They match — 9 and 9. Our answer was correct.
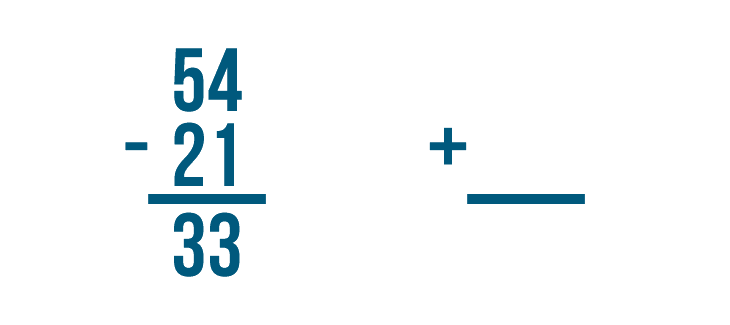
Let's try using addition to check the answer to another subtraction problem: 54 - 21 = 33.
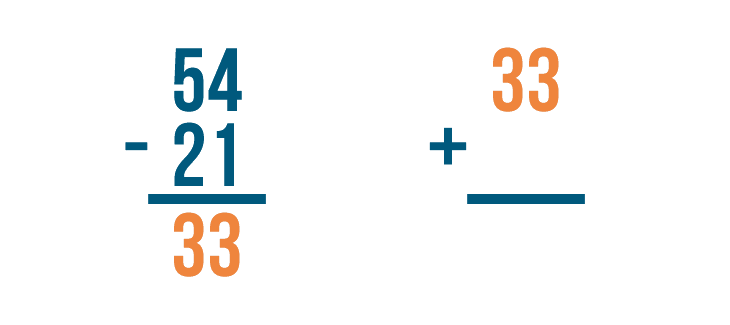
Let's set up our addition problem. First write the answer to the subtraction problem, 33.
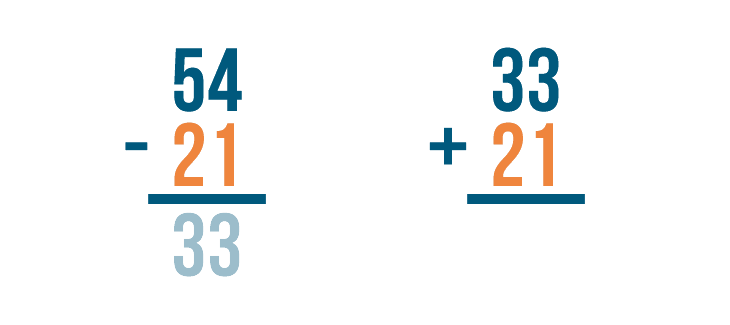
Then add back the number that was subtracted, 21.
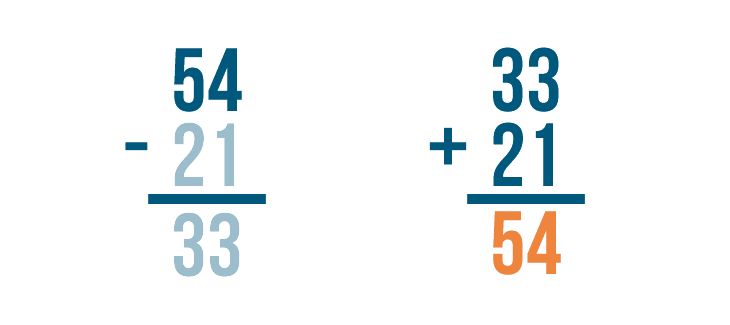
Now it's time to add. 33 + 21 = 54.
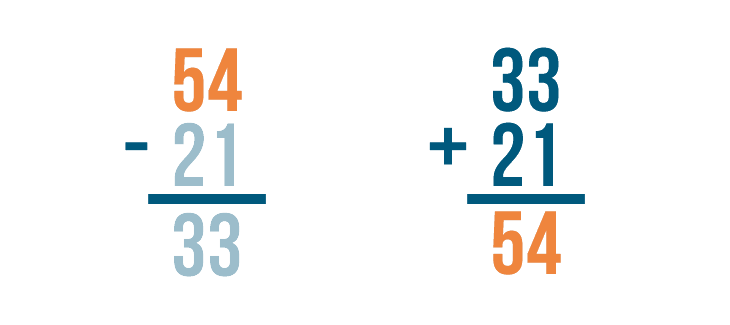
Finally, we'll check to see if 54 matches the larger number in our subtraction problem. It does!

Practice!
Practice subtracting these problems. You'll have to use borrowing to solve some of the problems. There are 4 sets of problems with 3 problems each.
Set 1
Set 2
Set 3
Set 4
/en/additionsubtraction/video-subtraction/content/





![]() mean the same thing — they're just written differently.
mean the same thing — they're just written differently.