When you're adding or subtracting decimal numbers, it's important to set up the expression correctly. The numbers need to be in a certain place, and so do the decimals.
Click through the slideshow below to learn how to set up these expressions.
Now that we know how to set up problems with decimals, let's practice by solving a few. First, we'll work on adding. If you feel comfortable adding larger numbers, you're ready to add decimal numbers.
Click through the slideshow to learn how to add decimals.
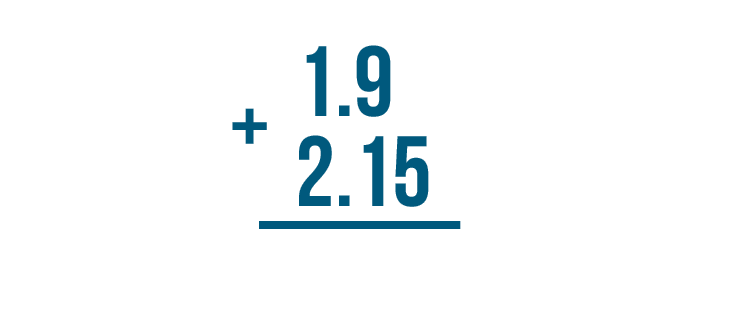
Let's try solving this problem: 1.9 + 2.15.
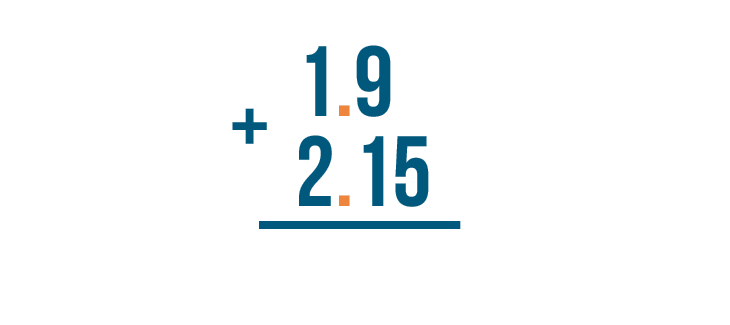
First, we'll make sure the decimals are lined up.
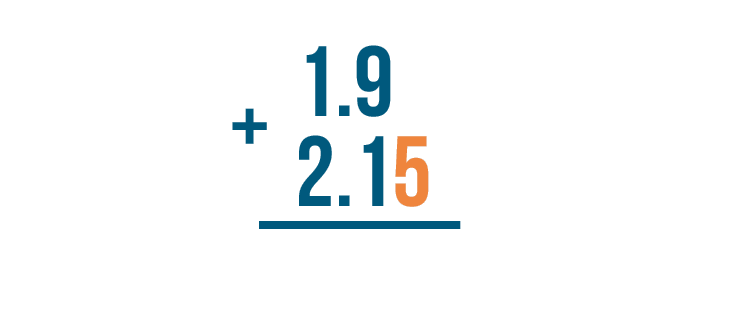
We'll start by adding the digits farthest to the right. In this case, we have nothing on top and 5 on the bottom.
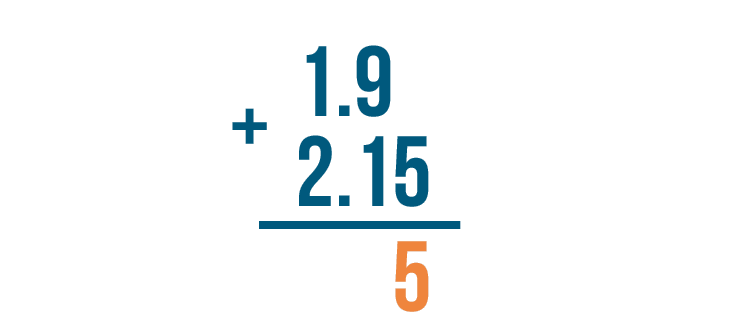
Nothing plus 5 equals 5. We'll write 5 beneath the line.
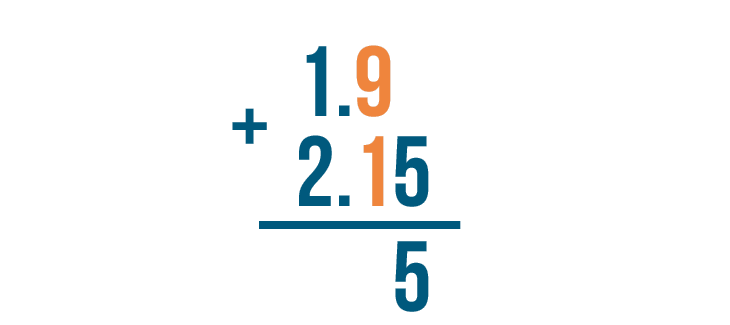
Now we'll add the next set of digits to the left: 9 and 1.
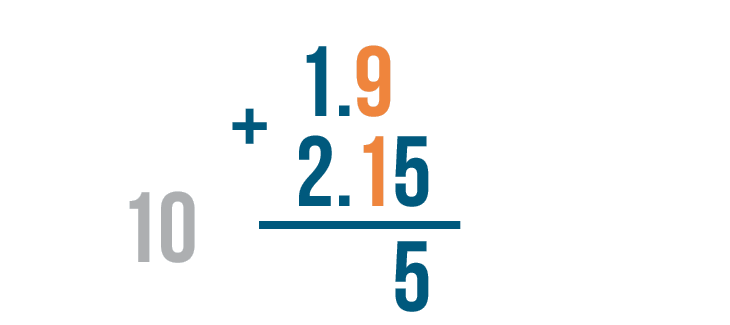
9 + 1 equals 10, but there's no room to write both digits in 10 underneath the 9 and 1. We'll have to carry.
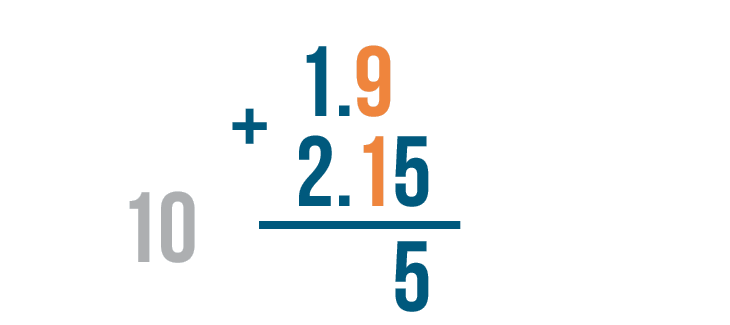
We learned how to carry numbers in the lesson on Adding Two- and Three-Digit Numbers.
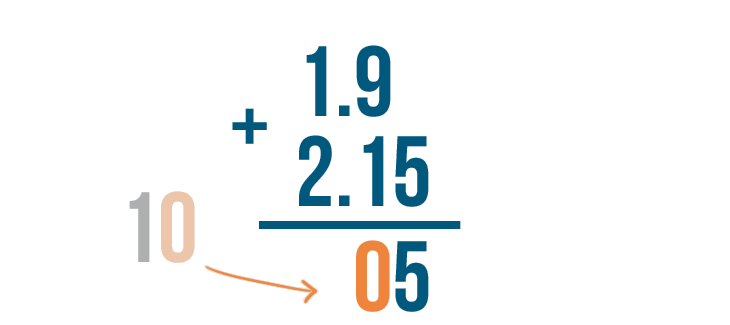
We'll write the right digit, 0, under the line...
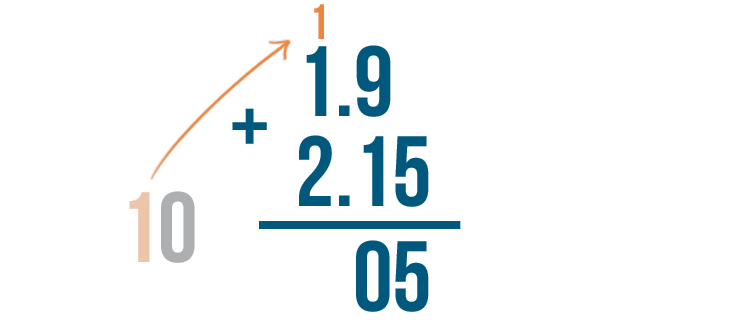
We'll write the right digit, 0, under the line...then we'll carry the left digit, 1, up to the next set of digits in the problem.
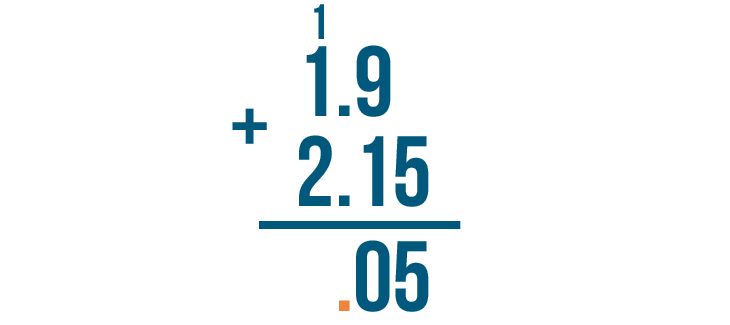
Now we'll write the decimal point. We'll place it directly beneath the other two decimal points.
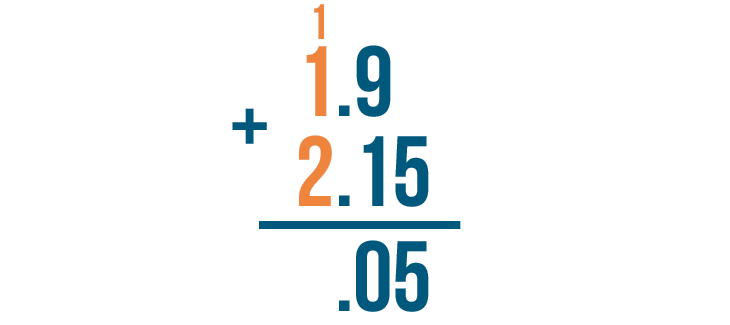
Next, we'll move left to add the next set of digits: 1 and 2. Since we carried the 1, we'll add it too.
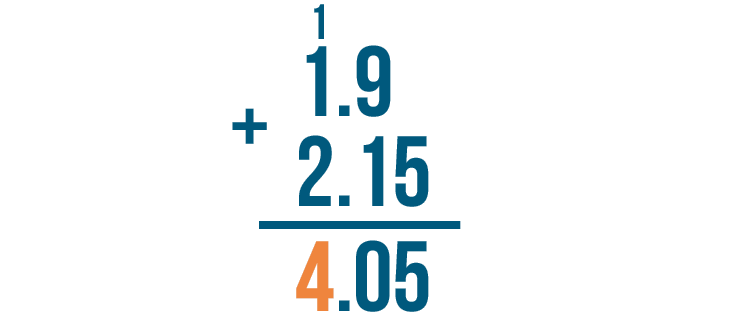
1 + 1 + 2 equals 4. We'll write 4 below the line.
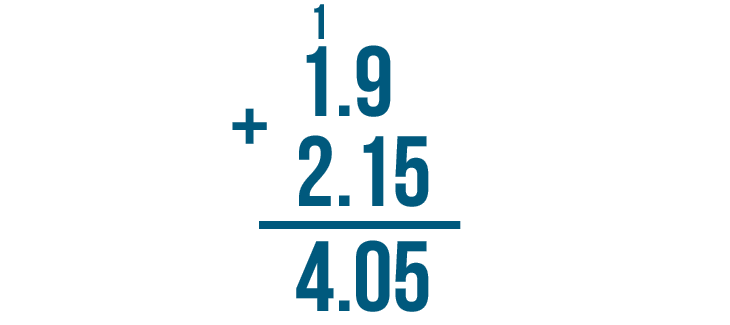
We're done. 1.9 + 2.15 = 4.05. We can read this answer as four and five-hundredths.
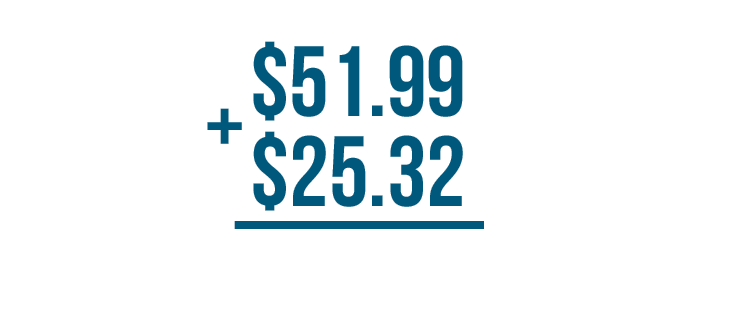
Let's try it with a money problem: $51.99 + $25.32.
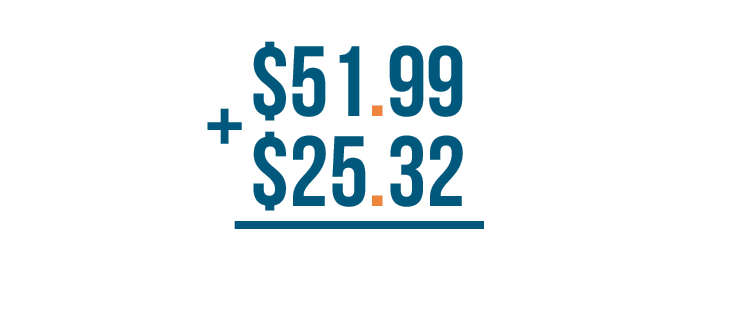
We'll make sure our decimal points are lined up properly.
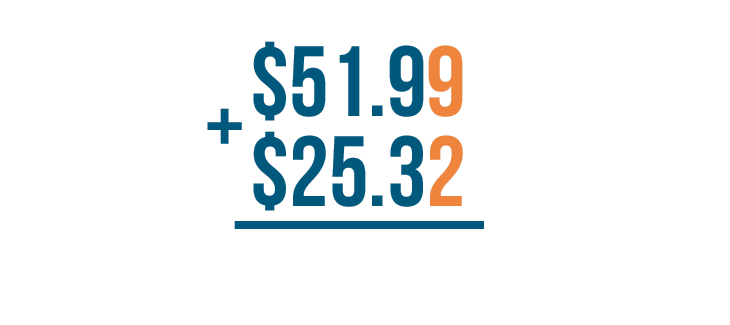
As always, we'll start by adding the digits on the right. Here, that's 9 and 2.
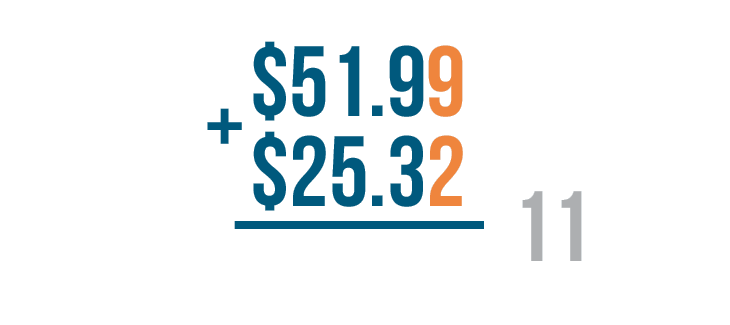
9 + 2 equals 11, so it looks like we'll have to carry.
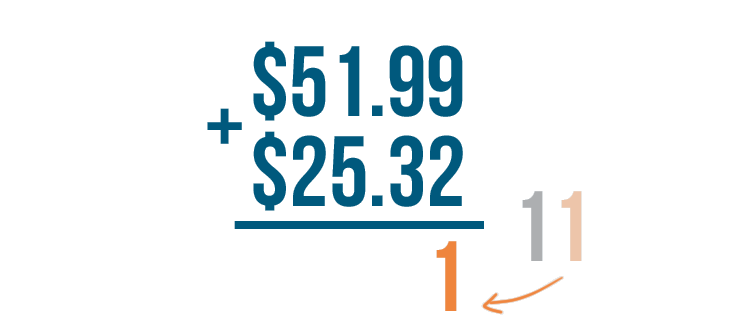
The 1 on the right stays underneath the 9 and the 2.
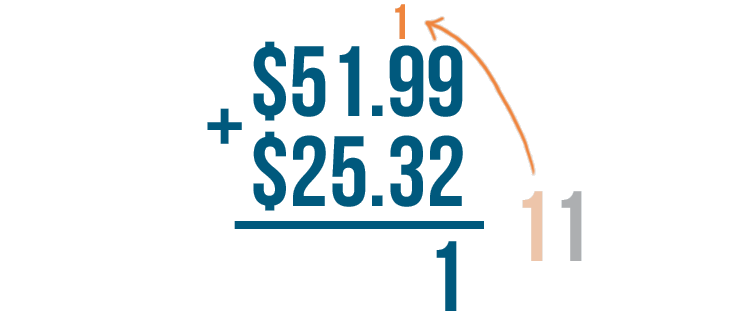
We'll carry the 1 on the left and place it above the next set of digits to the left.
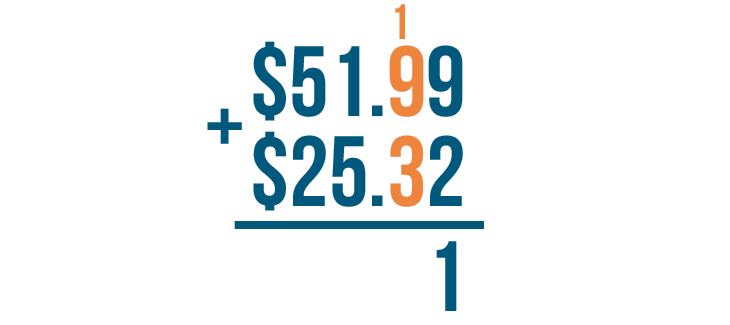
Now we'll move left to add the next set of digits. Since we carried the 1, we'll add it too.
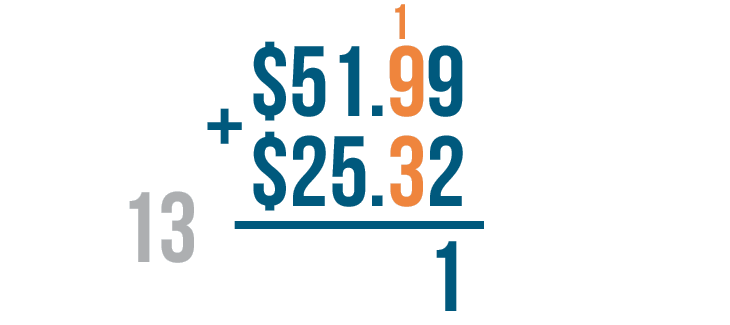
1 + 9 + 3 = 13.
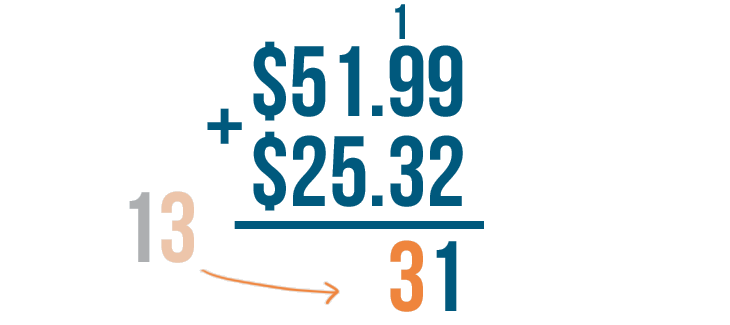
We'll put the 3 under the digits we added.
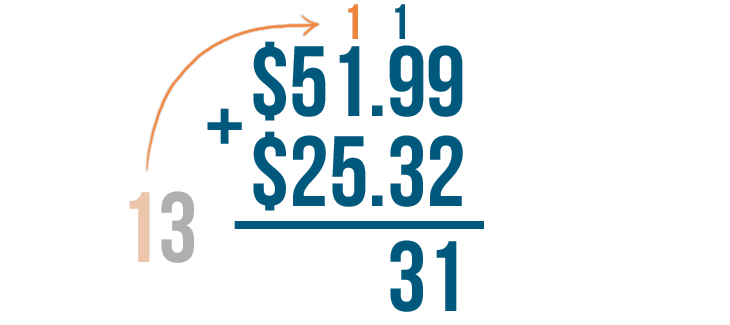
We'll carry the 1 and place it above the next column to the left.
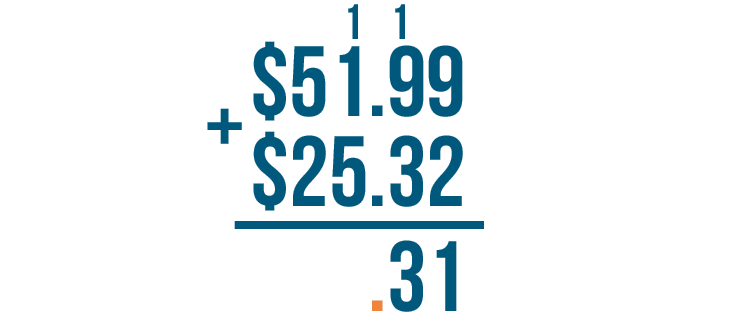
Now it's time to write the decimal point. Remember to place it directly beneath the other two decimal points.
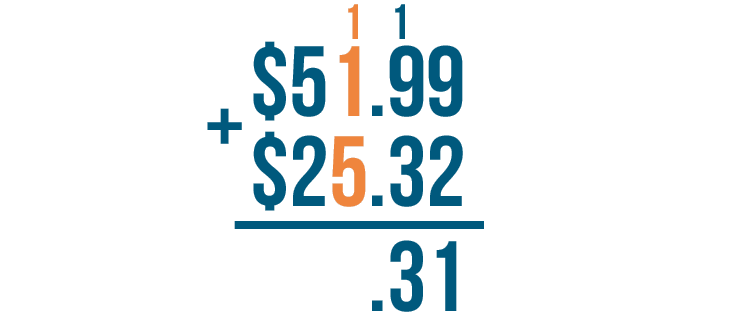
Next, we'll move left and add the next set of digits. We'll make sure to add the 1 we carried.
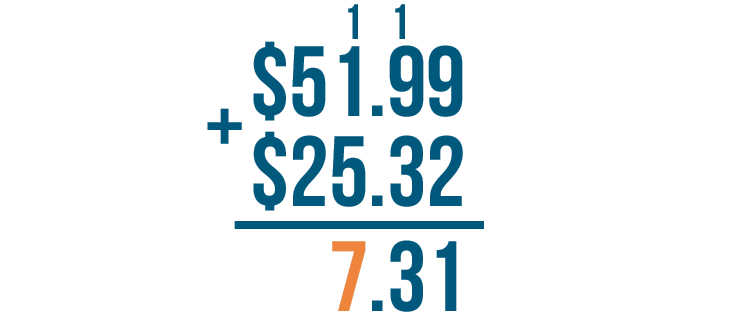
1 + 1 + 5 = 7. We'll write 7 beneath the line.
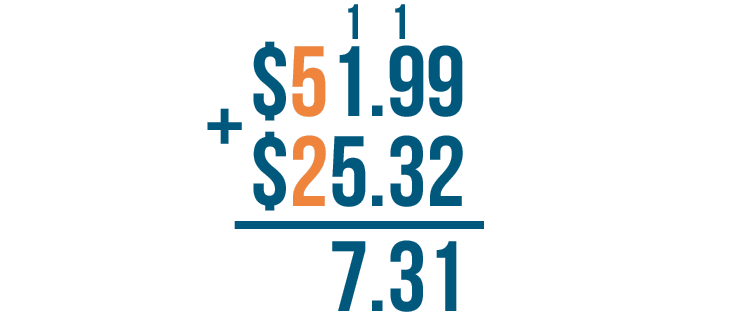
To finish, we'll add the next column to the left: 5 and 2.
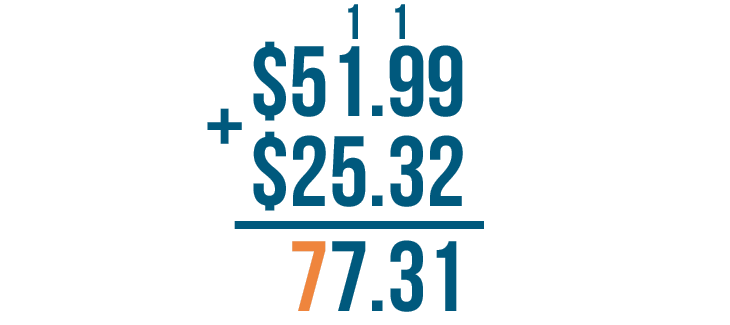
5 + 2 equals 7. We'll write 7 underneath the 2.
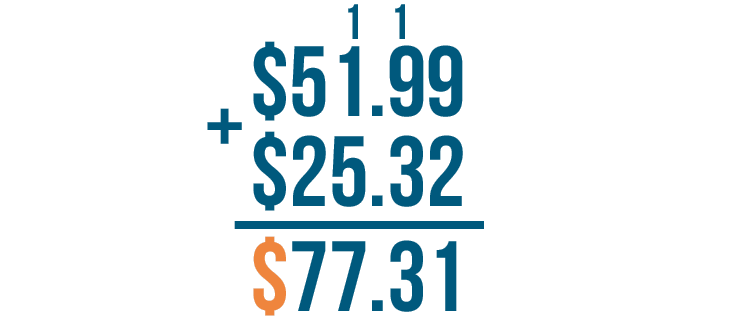
We'll finish by writing the dollar sign ($).
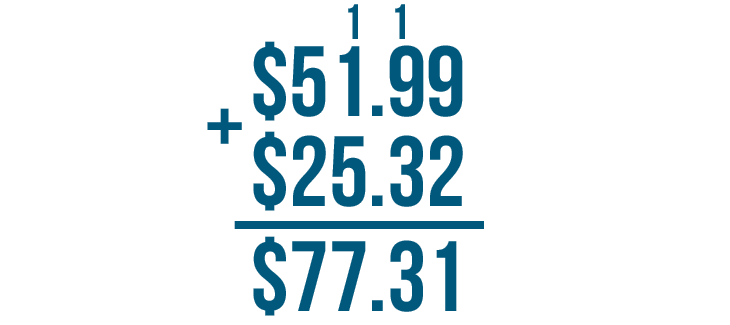
We're done. $51.99 + $25.32 = $77.31. We can read this answer as seventy-seven dollars and thirty-one cents.

Try solving these problems to practice adding decimal numbers.
Click through the slideshow to learn how to subtract decimals.

Let's try to solve this problem: 41.2 - 3.09.

First, we'll make sure the expression is set up correctly. Here, 41.2 is the larger number, so we'll put it on top.

The decimal points are lined up.

As always, we’ll begin with the digits farthest to the right. Here, we have nothing on top and 9 on the bottom.

We can’t take 9 away from nothing. We'll need to place a digit after 41.2 so we can subtract from it.

The value of our number won't change if we use the digit that means nothing: 0. We'll place a 0 after 41.2.

Now we can subtract the digits on the right. 0 is smaller than 9, so we’ll need to borrow to make 0 larger.

We learned how to borrow in the lesson on Subtracting Two- and Three-Digit Numbers.

We'll borrow from the digit to the left of 0. Here, it's 2. We'll take 1 from it.

2 - 1 = 1. To help us remember we subtracted 1, we'll cross out the 2 and write 1 above it.

Then we'll place the 1 we took next to the 0.

0 becomes 10.

10 is larger than 9, which means we can subtract. We'll solve for 10 - 9.
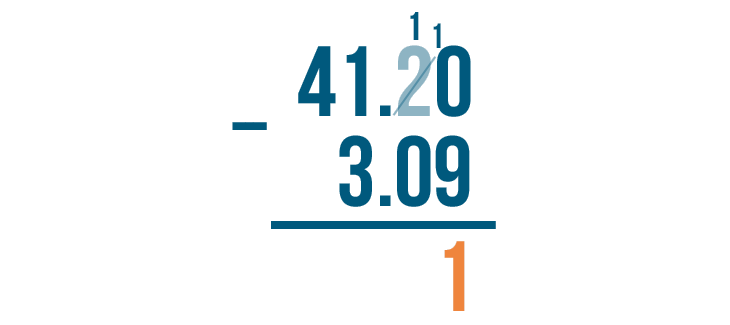
10 - 9 = 1. We'll write 1 beneath the line.

Now we'll move left to subtract the next set of digits: 1 - 0.
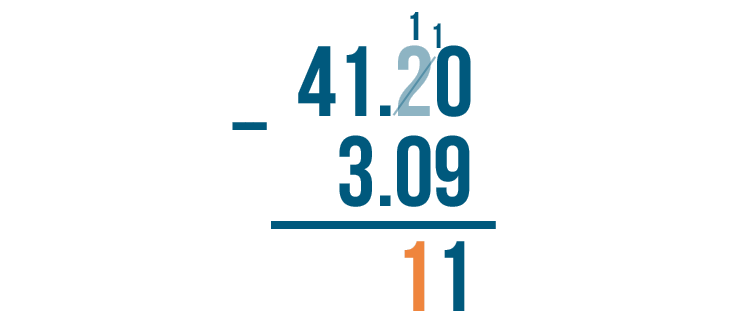
1 - 0 = 1. We'll write 1 beneath the line.
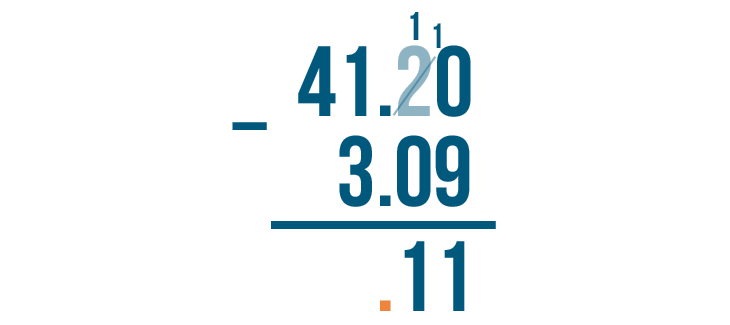
Now it's time to write the decimal point. We'll place it directly beneath the other two decimal points.
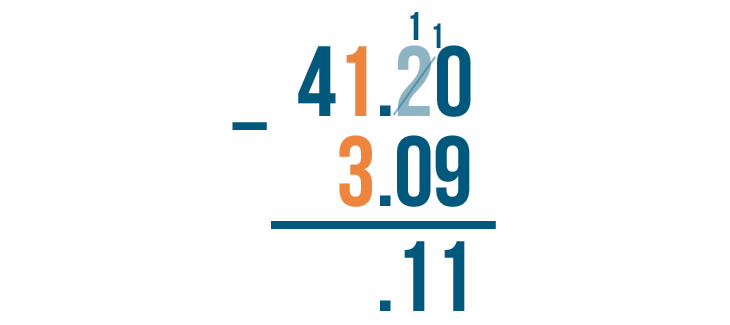
Now we'll find the difference of the next set of digits to the left: 1 - 3.
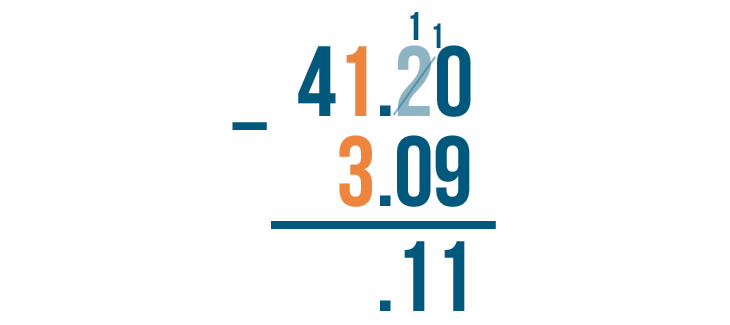
Because 1 is smaller than 3, it looks like we'll need to borrow again. We need to make the 1 larger.
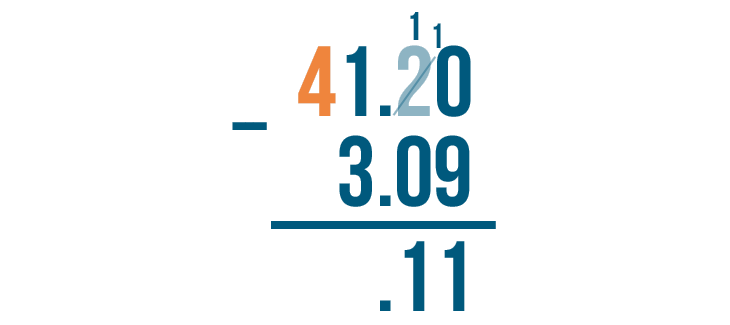
We'll borrow from the digit to the left of 1. Here, we'll borrow 1 from the 4.
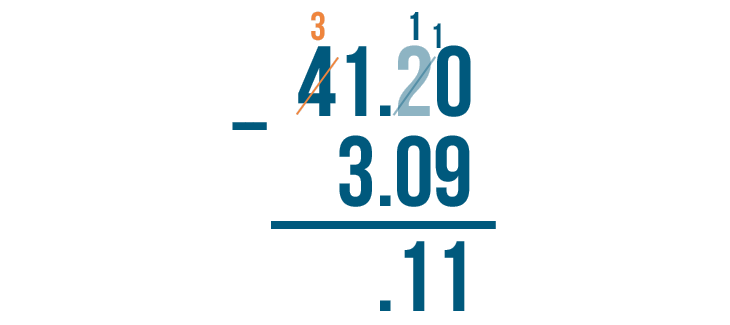
4 - 1 = 3. We'll write 3 above the 4.
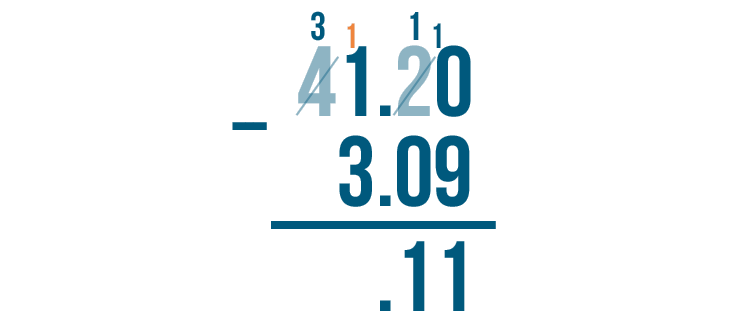
Then we'll place the 1 we took next to the 1.
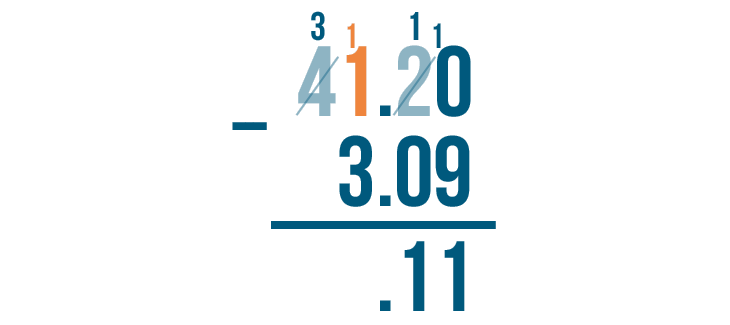
1 becomes 11.
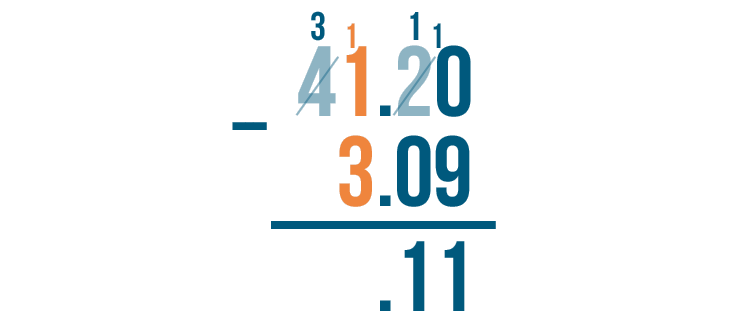
11 is larger than 3, which means we can subtract. We'll solve for 11 - 3.
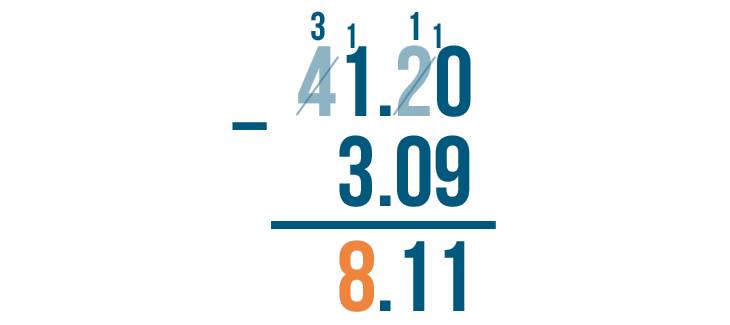
11 - 3 = 8. We'll write 8 beneath the line.
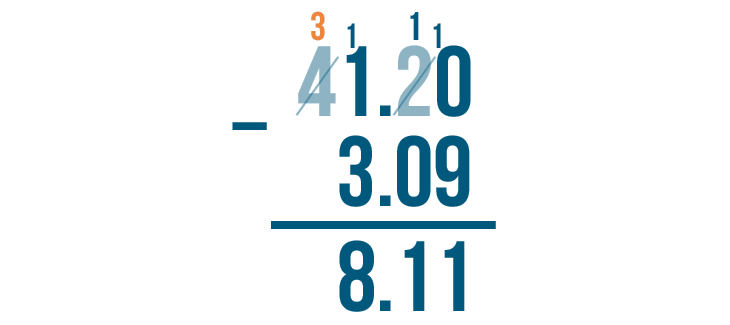
Finally, we'll move to the left to subtract the last set of digits. The top digit is 3, but there's nothing beneath it.
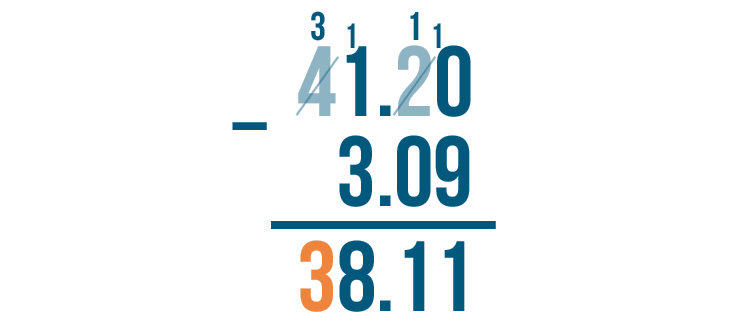
3 minus nothing equals 3, so we'll write 3 beneath the line.
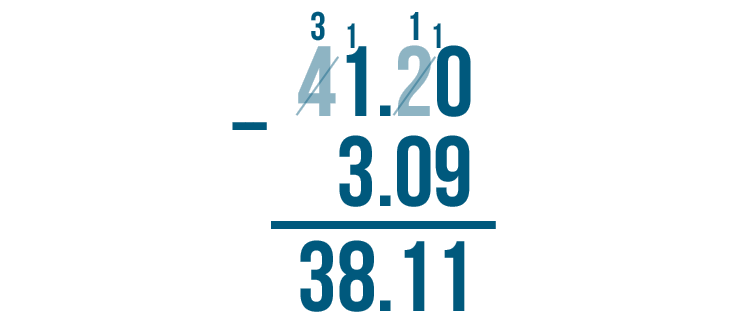
41.2 - 3.09 = 38.11. We can read this as thirty-eight and eleven-hundredths.
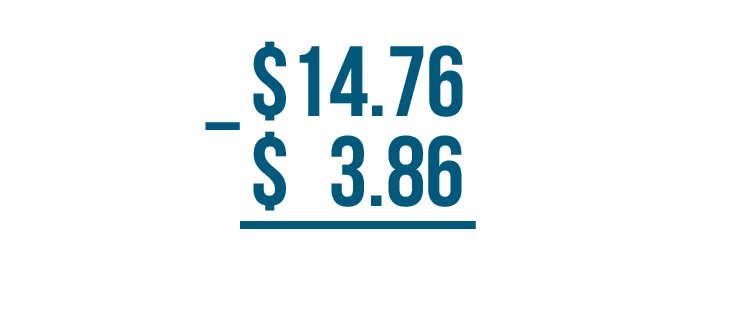
Let's try subtracting money. Let's see if we can solve $14.76 - $3.86.
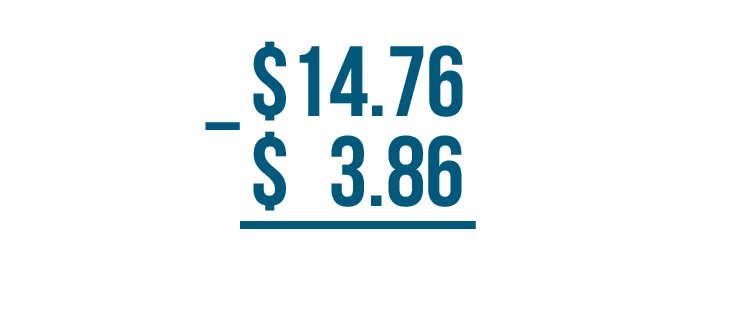
First, let's make sure the expression is set up correctly. The larger number is on top, and the decimal points are lined up.
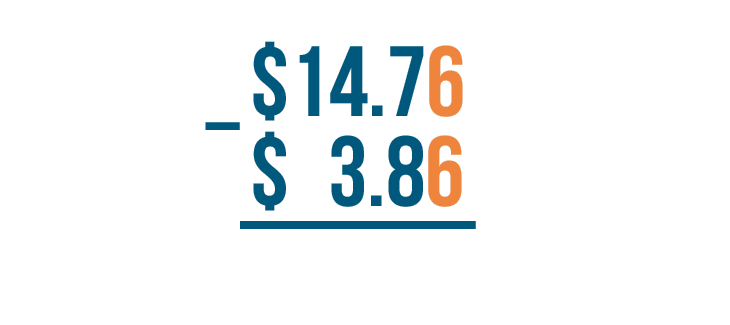
As always, let's start by finding the difference of the digits on the right. Here, that's 6 - 6.
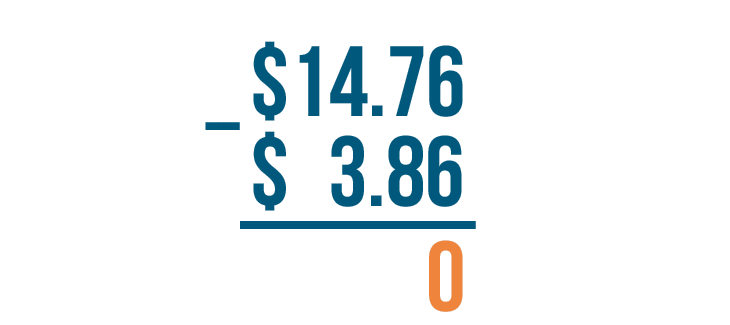
6 - 6 = 0. We'll write 0 beneath the line.
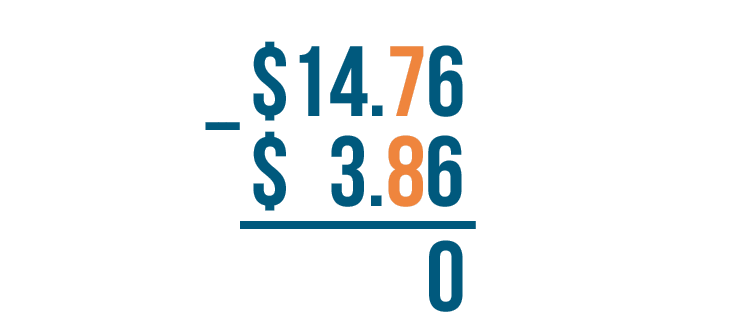
We'll move left to the next set of digits: 7 and 8. 7 is smaller than 8, so we'll borrow to make 7 larger.
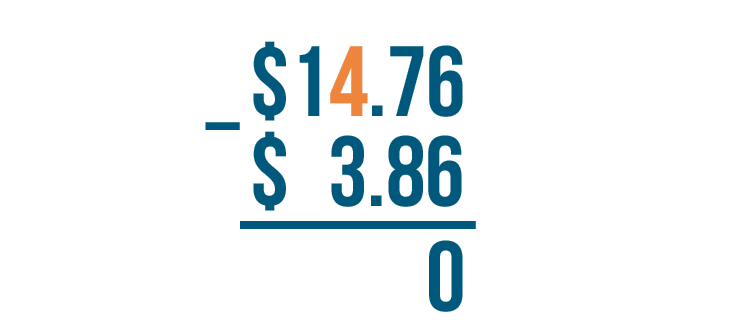
Let's look at the digit to the left of 7. Here, it's 4. We'll take 1 from it.
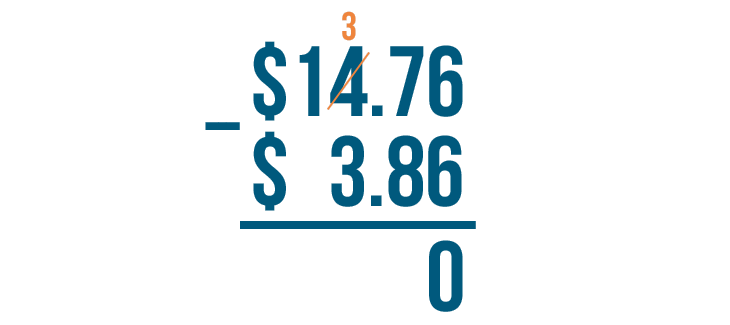
4 - 1 = 3. We'll cross out the 4 and write 3 above it.
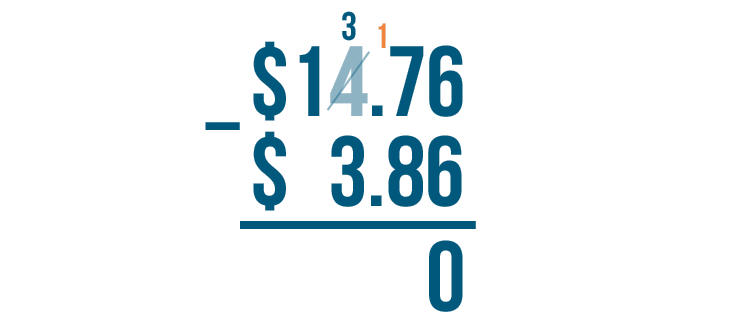
Then we'll place the 1 we took next to the 7.
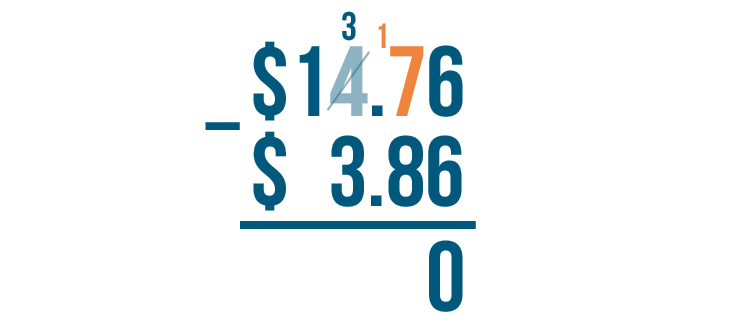
7 becomes 17.
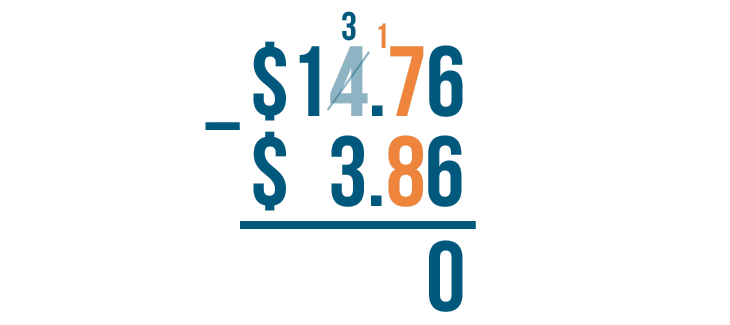
Now it's time to subtract. We'll solve for 17 - 8.
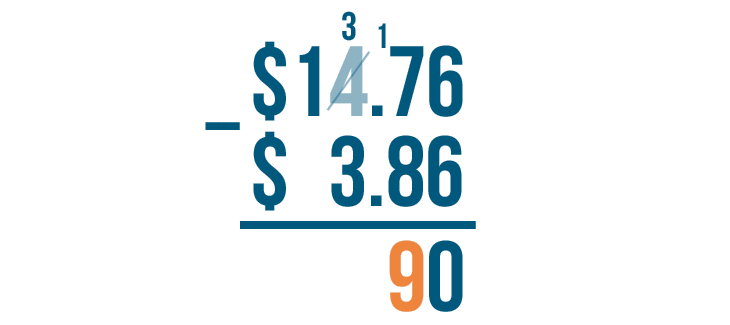
17 - 8 = 9. We'll write 9 beneath the line.
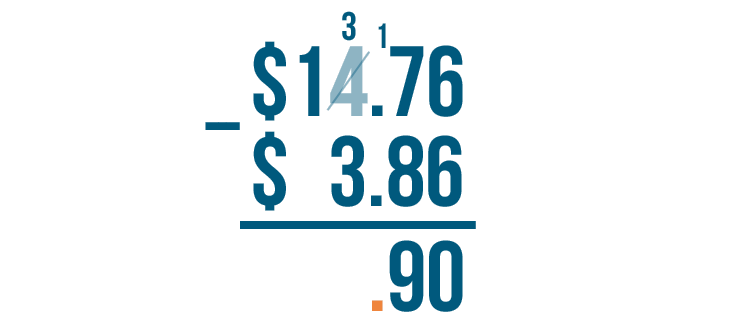
We'll put a decimal point directly beneath the other two decimal points.
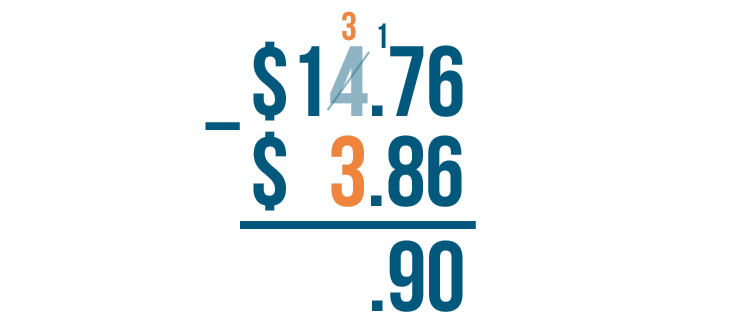
Next, we'll move left to find the difference of the next set of digits. Here, that's 3 - 3.
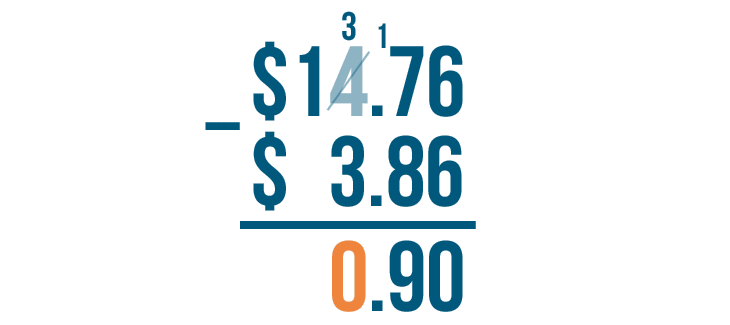
3 - 3 = 0. We'll write 0 below the line.
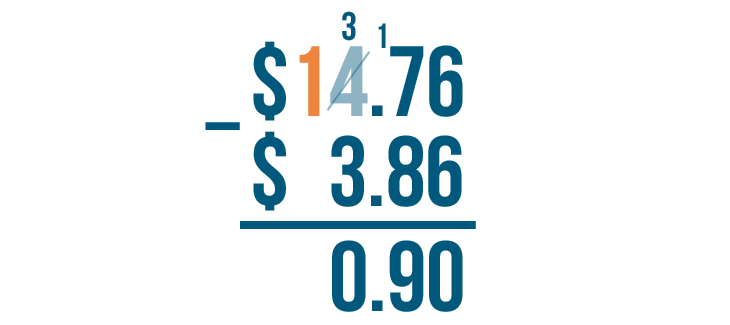
Finally, we'll move left to subtract the last set of digits. The top digit is 1, but there's nothing beneath it.
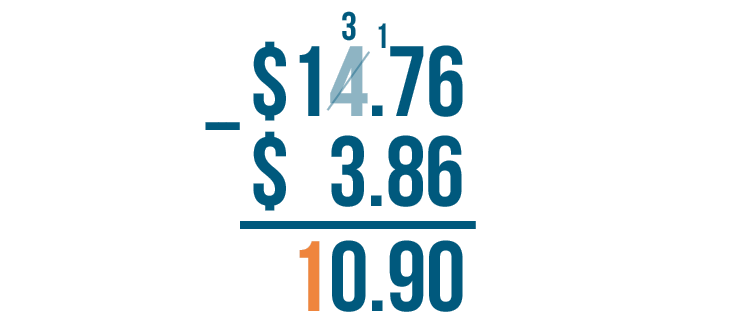
1 minus nothing equals 1. We'll write 1 beneath the line.
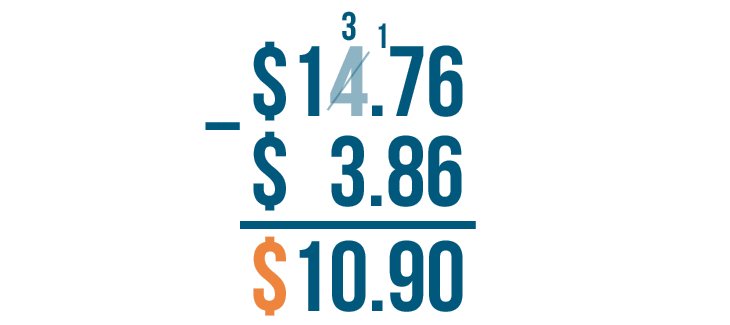
Next, we'll write a dollar sign ($) to the left of the 1.
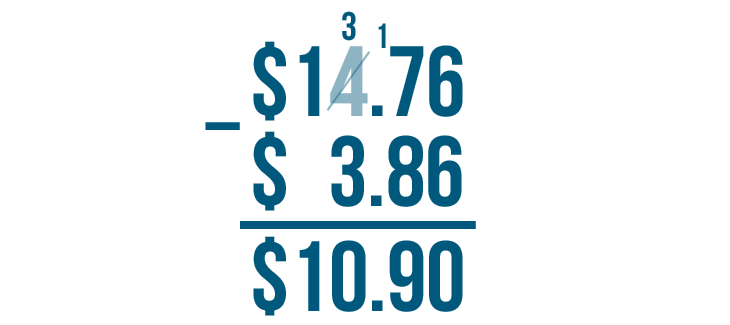
$14.76 - $3.86 = $10.90. We can read this as ten dollars and ninety cents.

Try solving these problems to practice subtracting decimal numbers.


