Excel Formulas -
Complex Formulas

Excel Formulas
Complex Formulas


/en/excelformulas/simple-formulas/content/
A simple formula is a mathematical expression with one operator, such as 7+9. A complex formula has more than one mathematical operator, such as 5+2*8. When there is more than one operation in a formula, the order of operations tells your spreadsheet which operation to calculate first. In order to use complex formulas, you will need to understand the order of operations.
Optional: Download our example file for this lesson.
Watch the video below to learn more about complex formulas.
All spreadsheet programs calculate formulas based on the following order of operations:
A mnemonic that can help you remember the order is PEMDAS, or Please Excuse My Dear Aunt Sally.
Click the arrows in the slideshow below to learn more about how the order of operations is used to calculate complex formulas.
Now let's look at a couple of examples that show how the order of operations can affect the result.
Using parentheses within a formula can be very important. Because of the order of operations, it can completely change an answer. Let's try the same problem from above, but this time we'll add parentheses to the last part.
In the example below, we'll demonstrate a complex formula using the order of operations. Here, we want to calculate the cost of sales tax for a catering invoice. To do this, we'll write our formula as =(D2+D3)*0.075 in cell D4. This formula will add the prices of our items together and then multiply that value by the 7.5% tax rate (which is written as 0.075) to calculate the cost of sales tax.
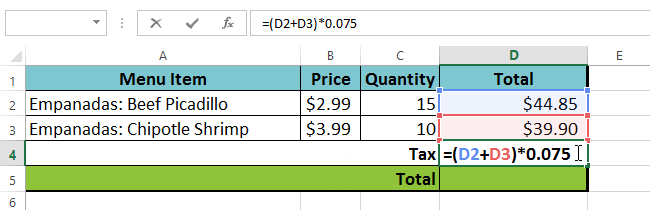
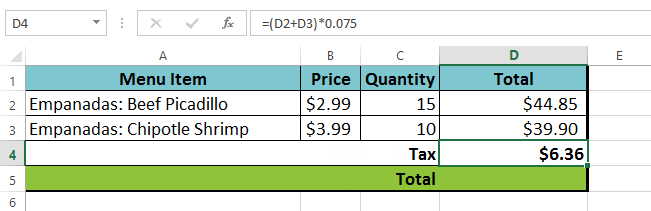
The spreadsheet then follows the order of operations and first adds the values inside the parentheses: (44.85+39.90) = $84.75. Then it multiplies that value by the tax rate: $84.75*0.075. The result will show that the sales tax is $6.36.
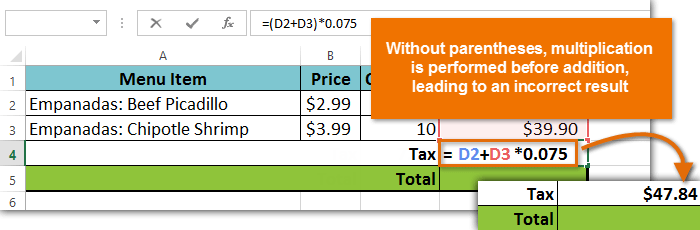
It is especially important to enter complex formulas with the correct order of operations. Otherwise, the spreadsheet will not calculate the results accurately. In our example, if the parentheses are not included, the multiplication is calculated first and the result is incorrect. Parentheses are the best way to define which calculations will be performed first in a formula.
In our example below, we will use cell references along with numerical values to create a complex formula that will calculate the total cost for a catering invoice. The formula will calculate the cost for each menu item and add those values together.
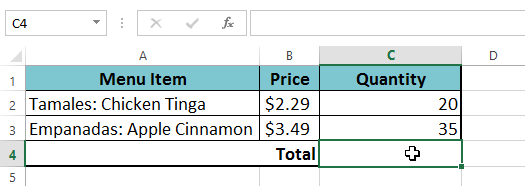
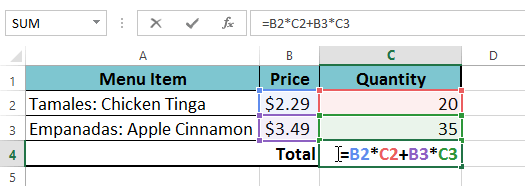
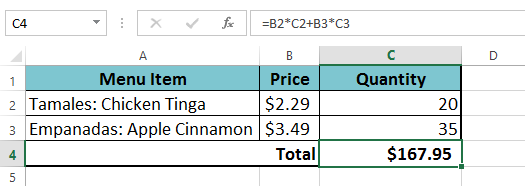
You can add parentheses to any equation to make it easier to read. While it won't change the result of the formula in this example, we could enclose the multiplication operations within parentheses to clarify that they will be calculated before the addition.
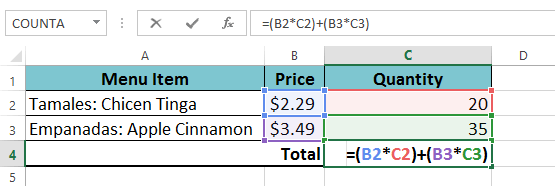
Your spreadsheet will not always tell you if your formula contains an error, so it's up to you to check all of your formulas. To learn how to do this, check out the Double-Check Your Formulas lesson.
/en/excelformulas/relative-and-absolute-cell-references/content/