Excel Formulas -
Percent-Off Sale

Excel Formulas
Percent-Off Sale


/en/excelformulas/overbudget-items/content/

Can you help me figure out how much it will cost after the discount? I added the basic info to a spreadsheet if that makes it any easier."
Once you've downloaded our spreadsheet, open the file in Excel or another spreadsheet application. Here, we have two main columns: one for the item name, and another for the item price. There's also a formula in cell B5 that calculates the original total cost of the items: =SUM(B2:B4)
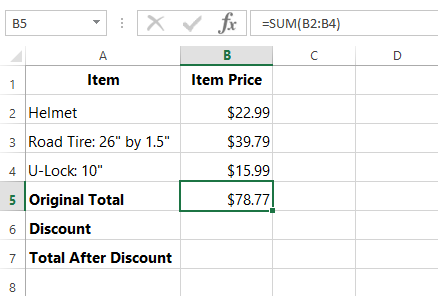
Let's think about the problem we're trying to solve. We want to know the total cost after the discount. A discount is a percentage of the original price. In this example, the discount is 15% of the original total.
To make this problem easier to solve with a spreadsheet, we'll break it down into two steps:
We know that we need a formula that will calculate 15% of $78.77. Whenever you see the phrase "of something" in a percentage problem, it's a hint that you need to multiply. So we'll need to multiply $78.77 by 15% to find the discount. When you're using percentages within formulas, you'll want to write them as decimals.
Excellent! Now that we know how to write 15% as a decimal, we're ready to write our formula:
=B5*0.15
We'll type this formula in cell B6 and then press Enter:
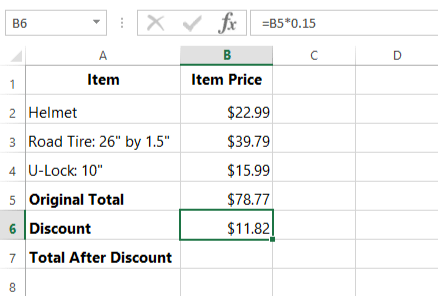
And here's our answer: The discount is $11.82.
Now that we've calculated our discount, we'll subtract that value from the original total. Here's our formula:
=B5-B6
We'll type this formula in cell B7 and press Enter:
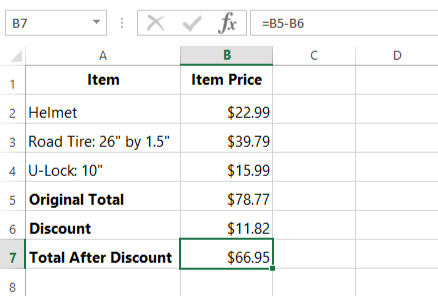
The final price after the discount will be $66.95.

Nice! I figured it'd be around that much, but I always like to know exactly how much I'm spending! Thanks so much—and let me know if you want to hit the bike trail soon!"
In the example above, we found the discount and then subtracted that from the original total. To make this simpler, we broke the problem down into two smaller steps. However, if you're comfortable working with percentage problems, we could have found the same answer with only one formula.
Can you figure out which formula we could have used instead? Here's a hint: Because we know we'll get 15% off, you could also say the final cost would be 85% of the original total.
/en/excelformulas/basketball-team-player-statistics/content/