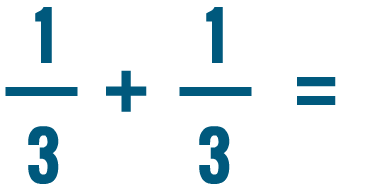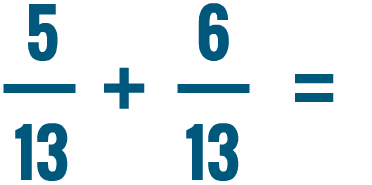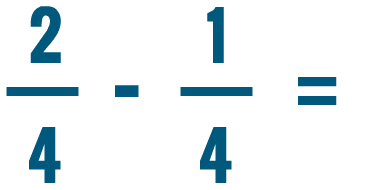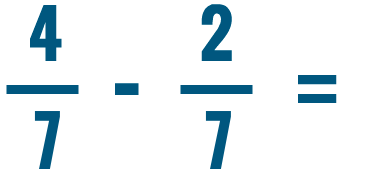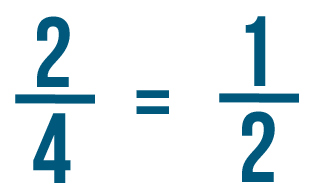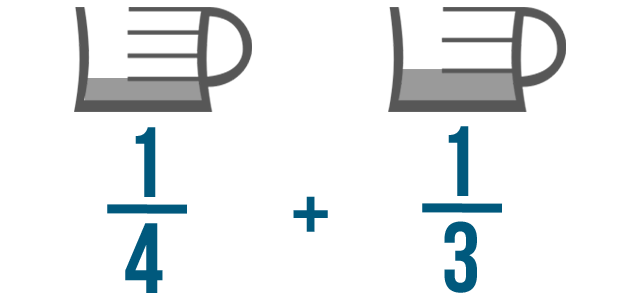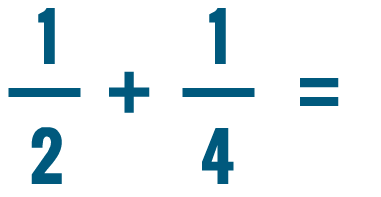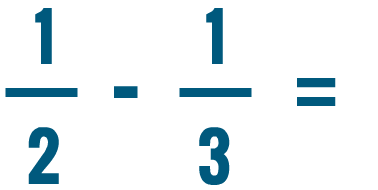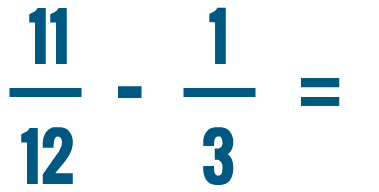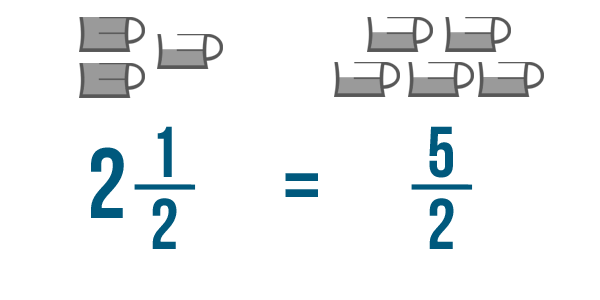Lesson 3: Adding and Subtracting Fractions
/en/fractions/comparing-and-reducing-fractions/content/
Adding and subtracting fractions
In the previous lessons, you learned that a fraction is part of a whole. Fractions show how much you have of something, like 1/2 of a tank of gas or 1/3 of a cup of water.
In real life, you might need to add or subtract fractions. For example, have you ever walked 1/2 of a mile to work and then walked another 1/2 mile back? Or drained 1/4 of a quart of gas from a gas tank that had 3/4 of a quart in it? You probably didn't think about it at the time, but these are examples of adding and subtracting fractions.
Click through the slideshow to learn how to set up addition and subtraction problems with fractions.

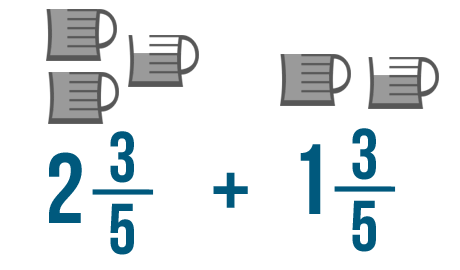
Let's imagine that a cake recipe tells you to add 3/5 of a cup of oil to the batter.

You also need 1/5 of a cup of oil to grease the pan. To see how much oil you'll need total, you can add these fractions together.
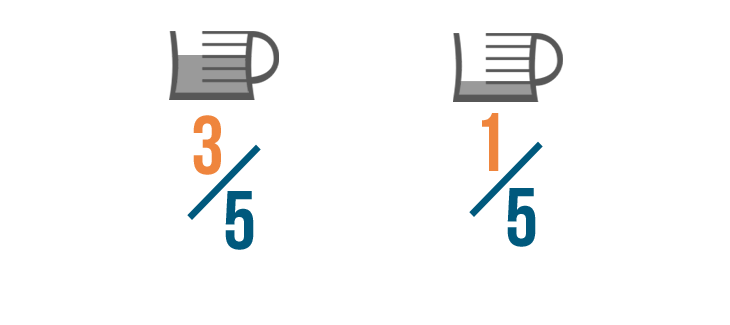
When you add fractions, you just add the top numbers, or numerators.
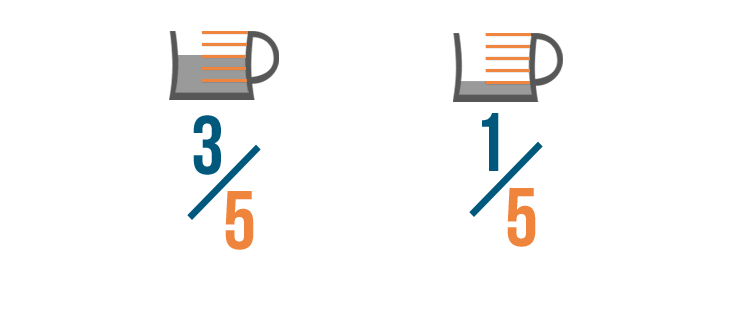
That's because the bottom numbers, or denominators, show how many parts would make a whole.

We don't want to change how many parts make a whole cup (5). We just want to find out how many parts we need total.
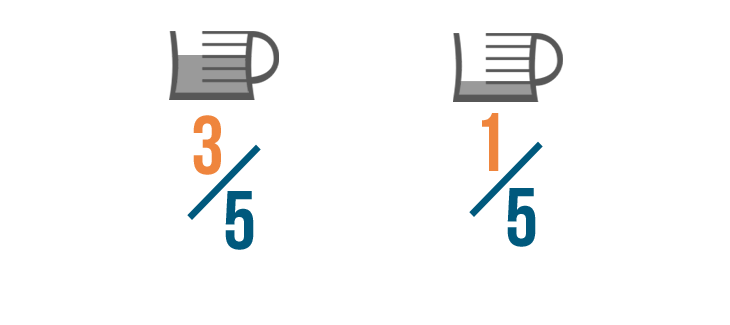
So we only need to add the numerators of our fractions.
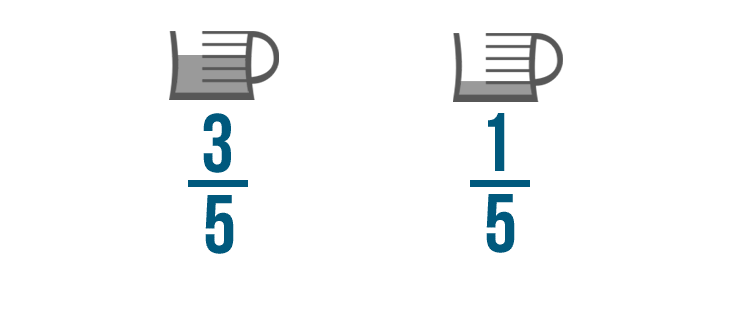
We can stack the fractions so the numerators are lined up. This will make it easier to add them.
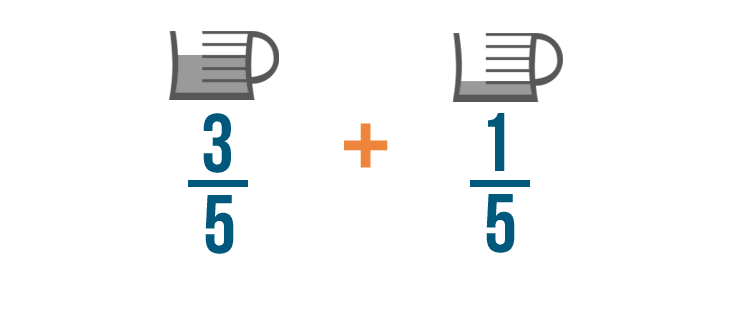
And that's all we have to do to set up an addition example with fractions. Our fractions are now ready to be added.

We'll do the same thing to set up a subtraction example. Let's say you had 3/4 of a tank of gas when you got to work.
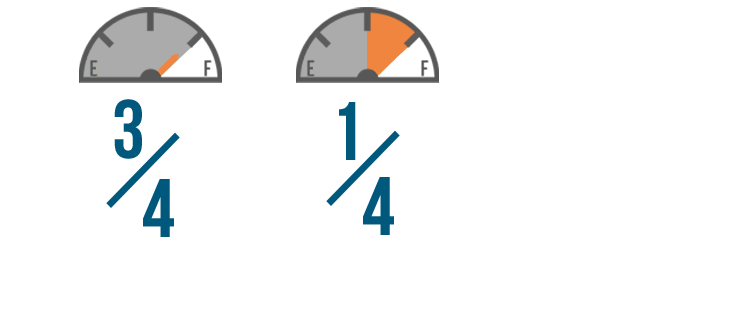
If you use 1/4 of a tank to drive home, how much will you have left? We can subtract these fractions to find out.
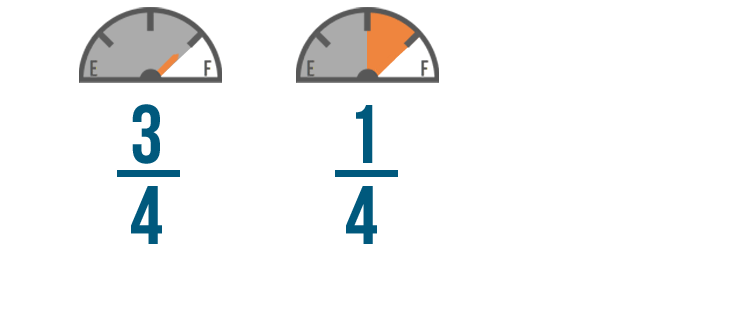
Just like when we added, we'll stack our fractions to keep the numerators lined up.
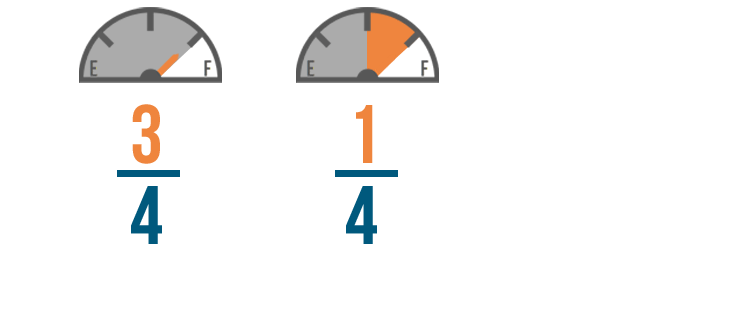
This is because we want to subtract 1 part from 3 parts.
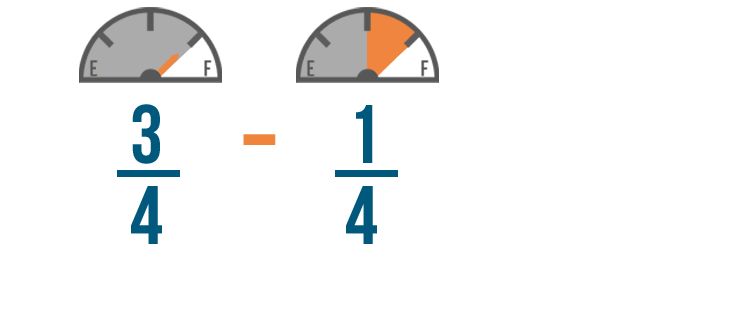
Now that our example is set up, we're ready to subtract!

Try This!
Try setting up these addition and subtraction problems with fractions. Don't try solving them yet!
You run 4/10 of a mile in the morning. Later, you run for 3/10 of a mile.
You had 7/8 of a stick of butter and used 2/8 of the stick while cooking dinner.
Your gas tank is 2/5 full, and you put in another 2/5 of a tank.
Solving addition problems with fractions
Now that we know how to write addition problems with fractions, let's practice solving a few. If you can add whole numbers, you're ready to add fractions.
Click through the slideshow to learn how to add fractions.
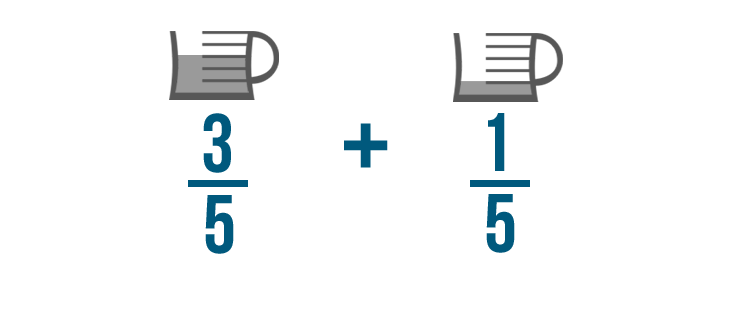
Let's continue with our previous example and add these fractions: 3/5 of cup of oil and 1/5 of a cup of oil.
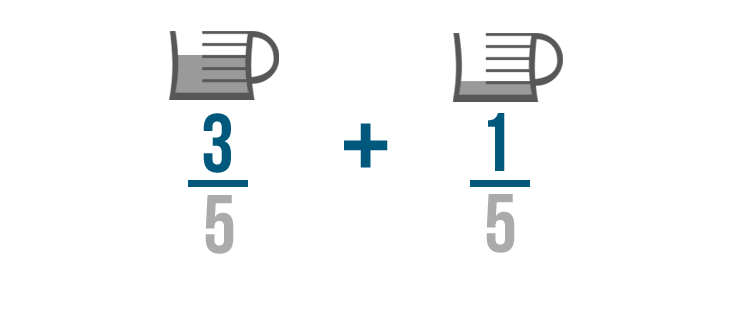
Remember, when we add fractions, we don't add the denominators.
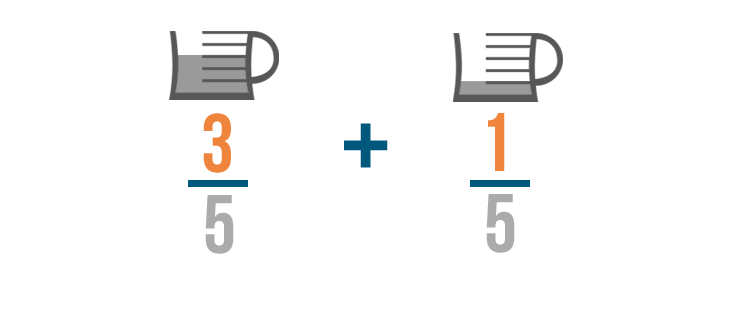
This is because we're finding how many parts we need total. The numerators show the parts we need, so we'll add 3 and 1.
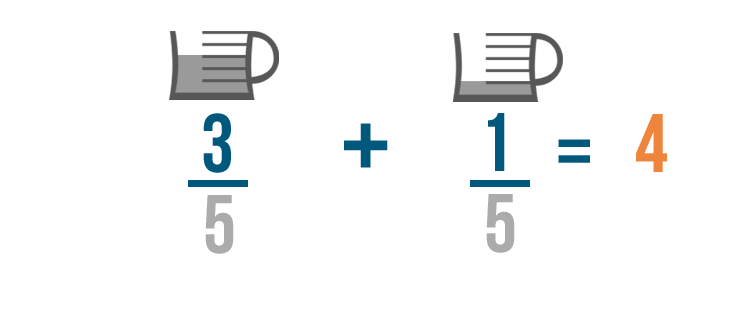
3 plus 1 equals 4. Make sure to line up the 4 with the numbers you just added.
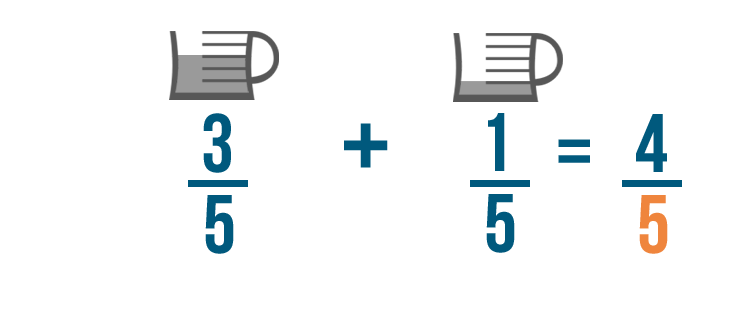
The denominators will stay the same, so we'll write 5 on the bottom of our new fraction.
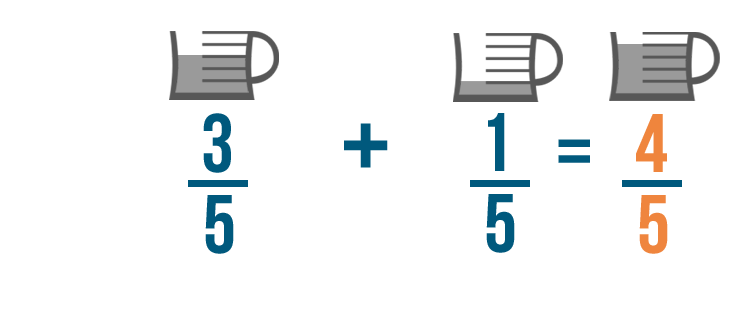
3/5 plus 1/5 equals 4/5. So you'll need 4/5 of a cup of oil total to make your cake.
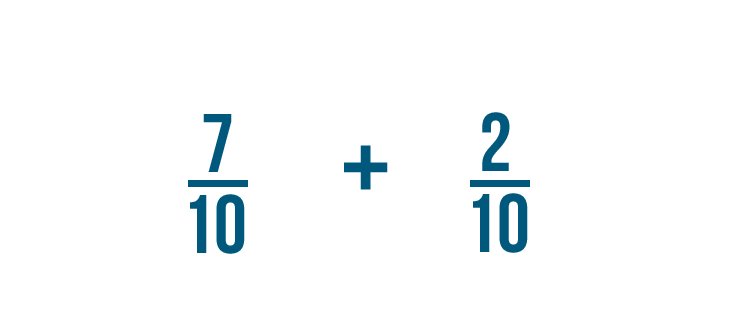
Let's try another example: 7/10 plus 2/10.
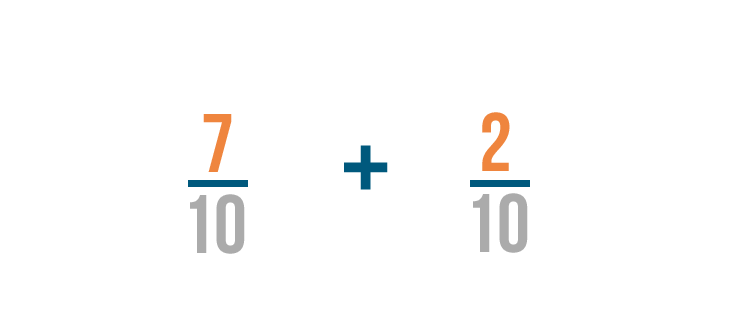
Just like before, we're only going to add the numerators. In this example, the numerators are 7 and 2.
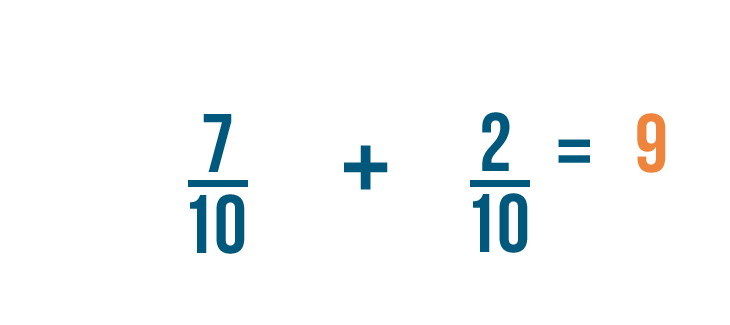
7 plus 2 equals 9, so we'll write that to the right of the numerators.
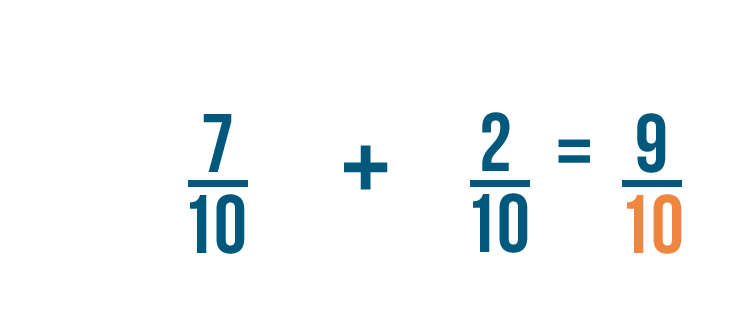
Just like in our earlier example, the denominator stays the same.
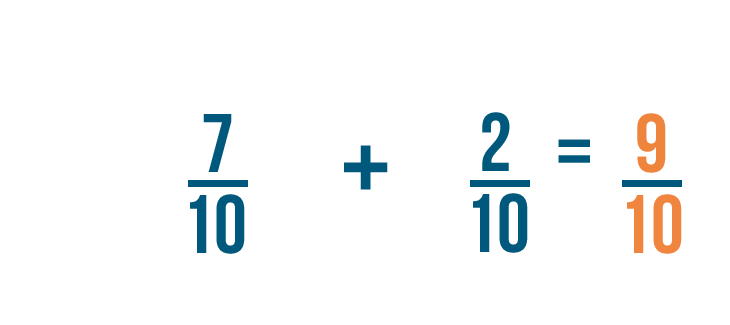
So 7/10 plus 2/10 equals 9/10.

Try This!
Try solving some of the addition problems below.
Solving subtraction problems with fractions
Subtracting fractions is a lot like regular subtraction. If you can subtract whole numbers, you can subtract fractions too!
Click through the slideshow to learn how to subtract fractions.
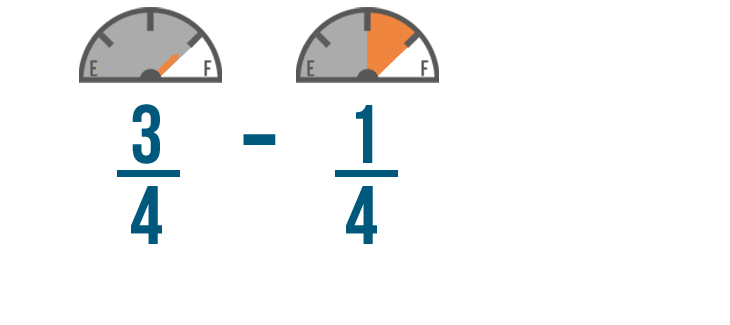
Let's use our earlier example and subtract 1/4 of a tank of gas from 3/4 of a tank.
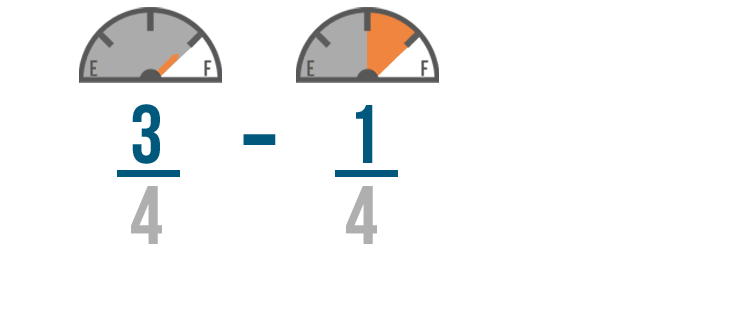
Just like in addition, we're not going to change the denominators.
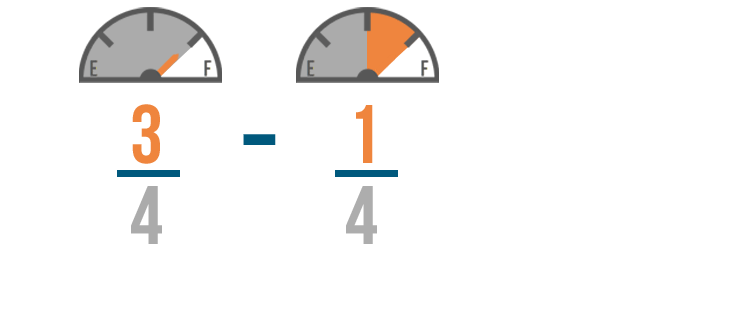
We don't want to change how many parts make a whole tank of gas. We just want to know how many parts we'll have left.
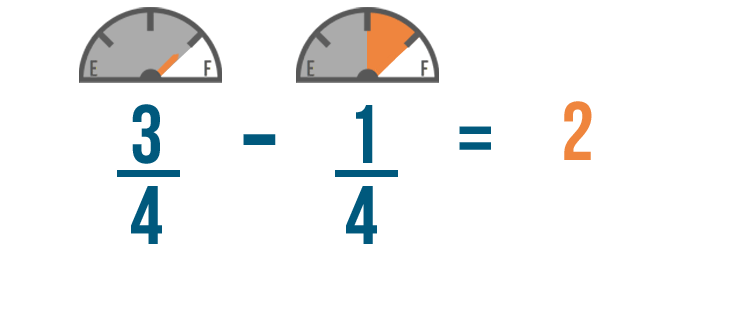
We'll start by subtracting the numerators. 3 minus 1 equals 2, so we'll write 2 to the right of the numerators.
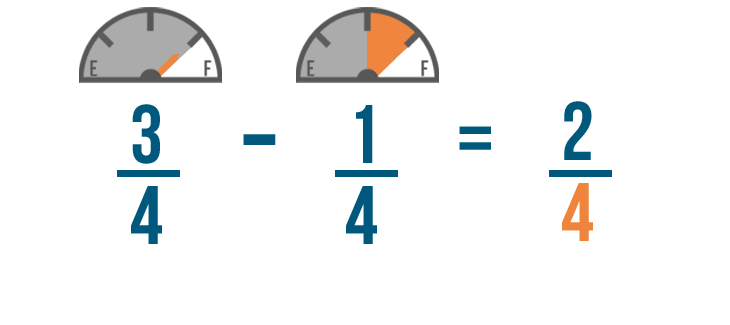
Just like when we added, the denominator of our answer will be the same as the other denominators.
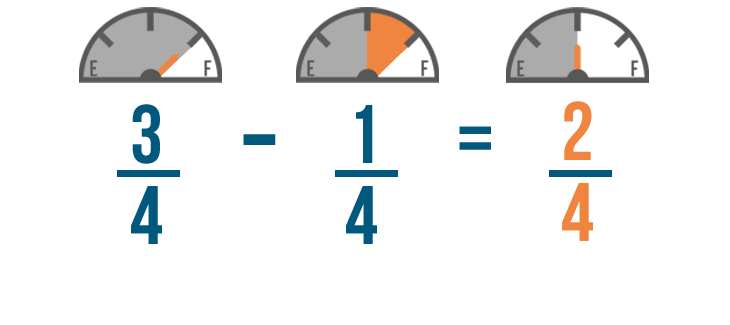
So 3/4 minus 1/4 equals 2/4. You'll have 2/4 of a tank of gas left when you get home.
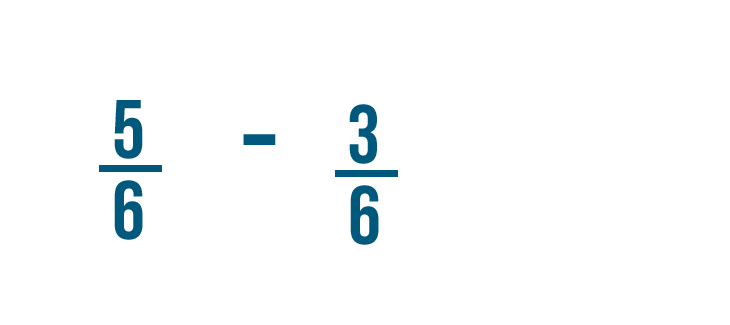
Let's try solving another problem: 5/6 minus 3/6.
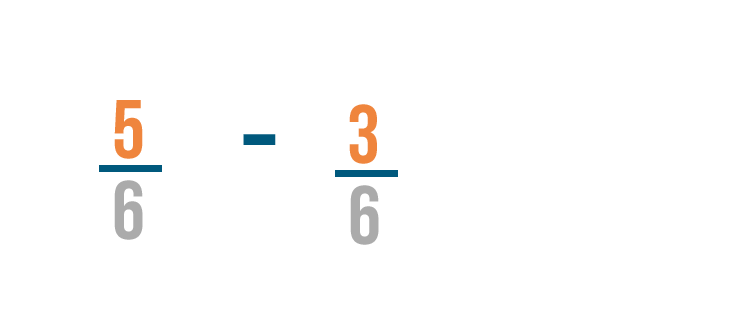
We'll start by subtracting the numerators.
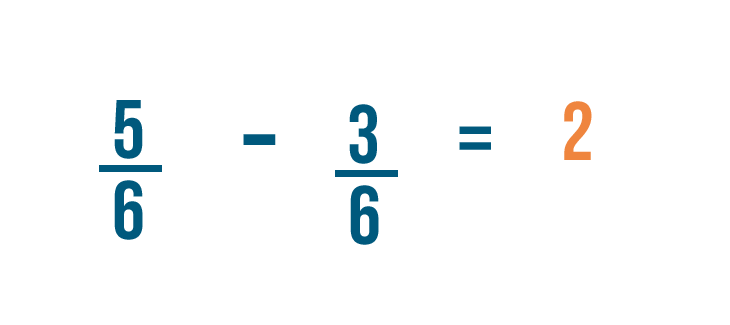
5 minus 3 equals 2. So we'll put a 2 to the right of the numerators.
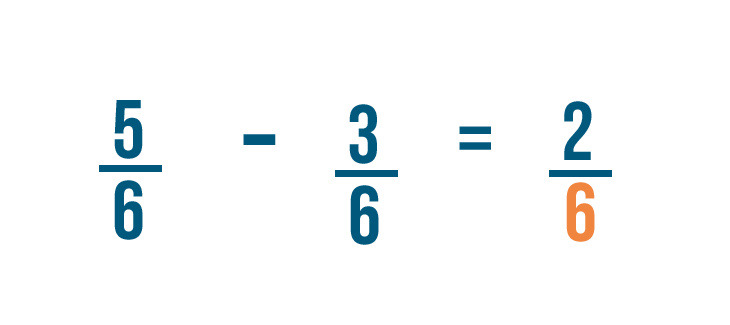
As usual, the denominator stays the same.
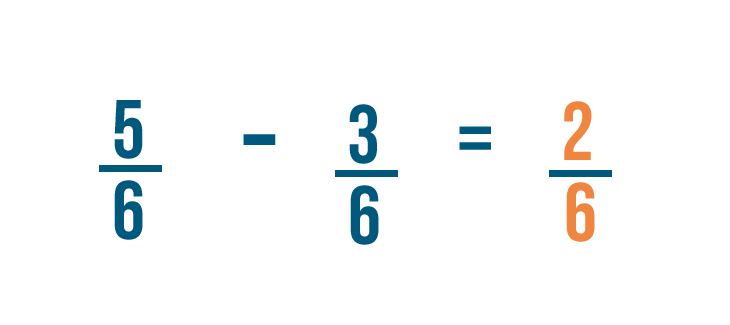
So 5/6 minus 3/6 equals 2/6.

Try This!
Try solving some of the subtraction problems below.
After you add or subtract fractions, you may sometimes have a fraction that can be reduced to a simpler fraction. As you learned in Comparing and Reducing Fractions, it's always best to reduce a fraction to its simplest form when you can. For example, 1/4 plus 1/4 equals 2/4. Because 2 and 4 can both be divided 2, we can reduce 2/4 to 1/2.
Adding fractions with different denominators
On the last page, we learned how to add fractions that have the same denominator, like 1/4 and 3/4. But what if you needed to add fractions with different denominators? For example, our cake recipe might say to blend 1/4 cup of milk in slowly and then dump in another 1/3 of a cup.
In Comparing and Reducing Fractions, we compared fractions with a different bottom number, or denominator. We had to change the fractions so their denominators were the same. To do that, we found the lowest common denominator, or LCD.
We can only add or subtract fractions if they have the same denominators. So we'll need to find the lowest common denominator before we add or subtract these fractions. Once the fractions have the same denominator, we can add or subtract as usual.
Click through the slideshow to learn how to add fractions with different denominators.
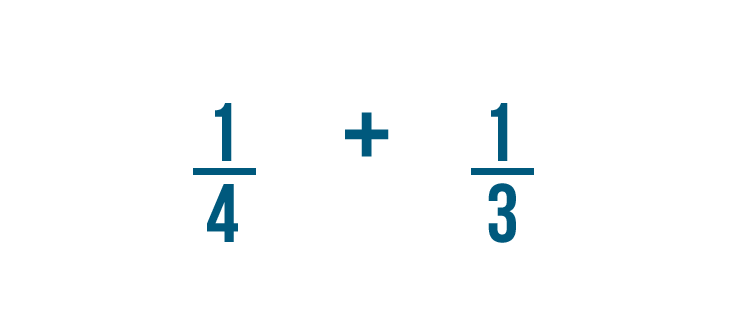
Let's add 1/4 and 1/3.
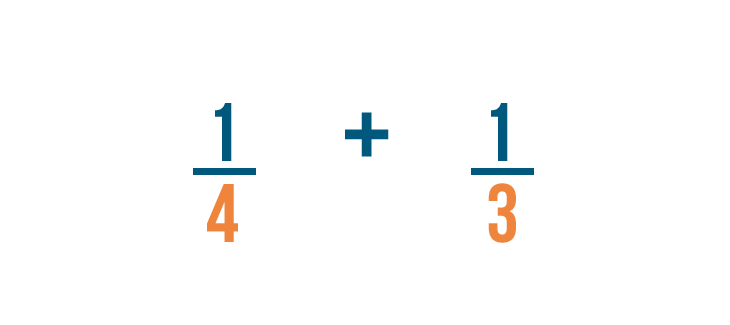
Before we can add these fractions, we'll need to change them so they have the same denominator.
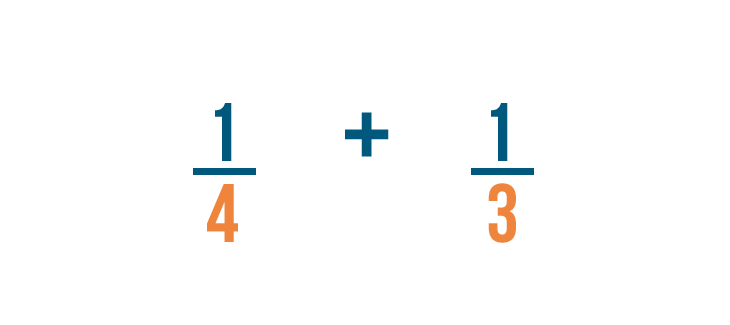
To do that, we'll have to find the LCD, or lowest common denominator, of 4 and 3.
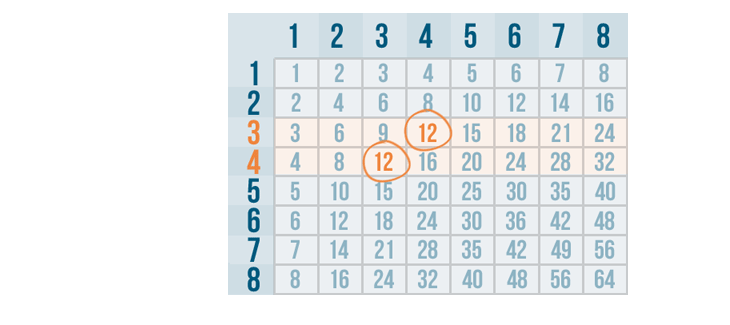
It looks like 12 is the smallest number that can be divided by both 3 and 4, so 12 is our LCD.
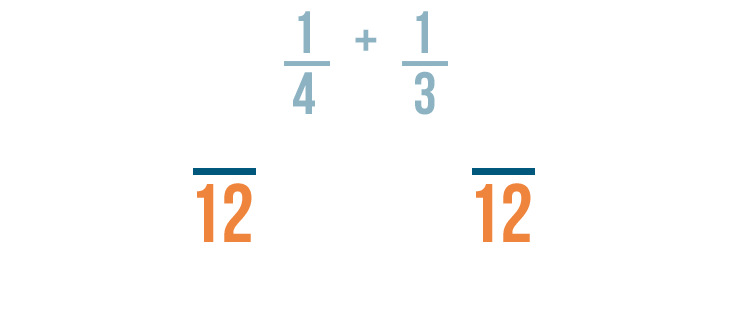
Since 12 is the LCD, it will be the new denominator for our fractions.
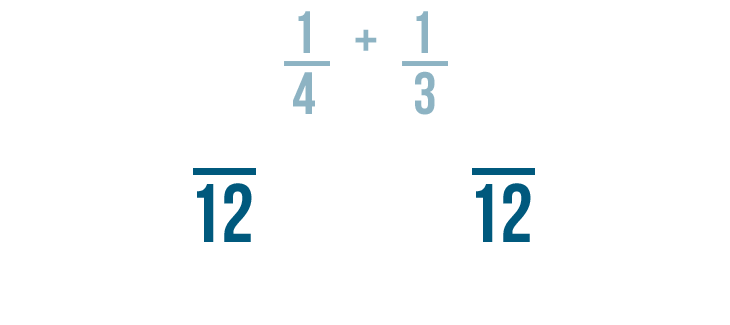
Now we'll change the numerators of the fractions, just like we changed the denominators.
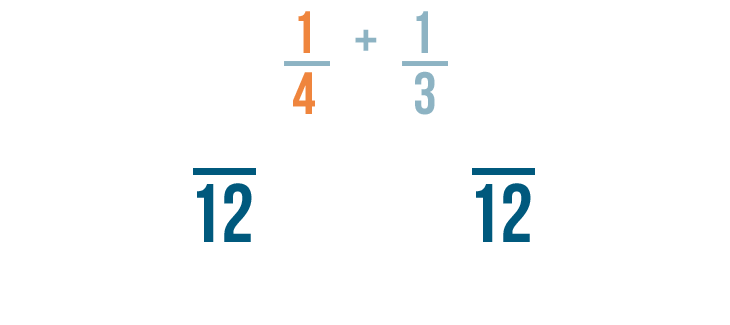
First, let's look at the fraction on the left: 1/4.
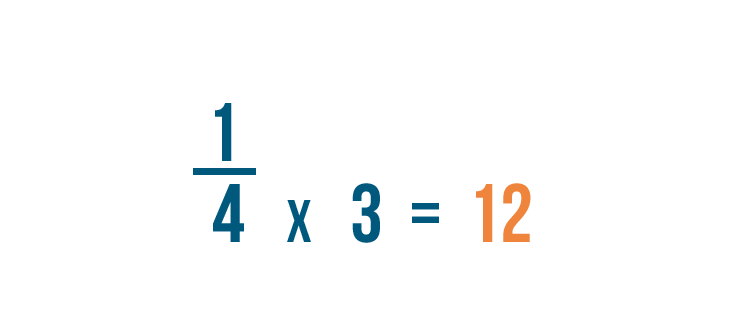
To change 4 into 12, we multiplied it by 3.
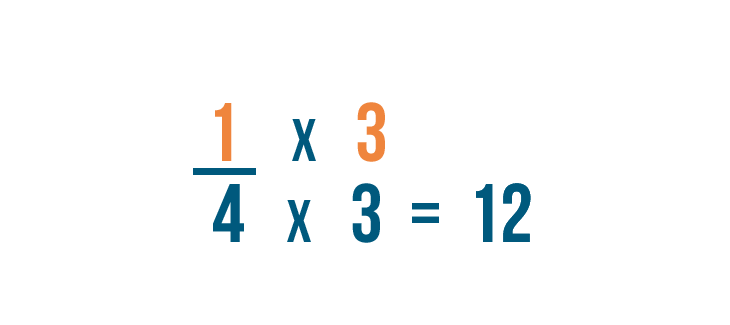
Since the denominator was multiplied by 3, we'll also multiply the numerator by 3.
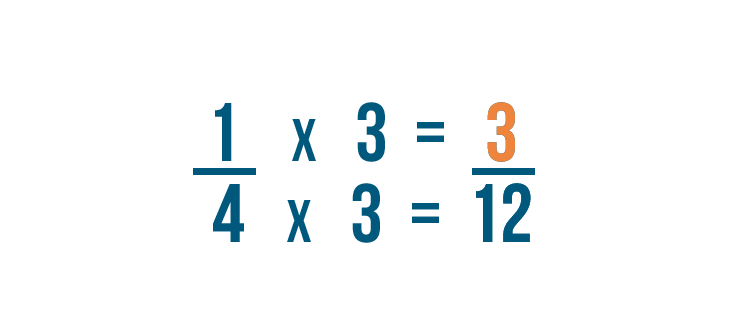
1 times 3 equals 3.
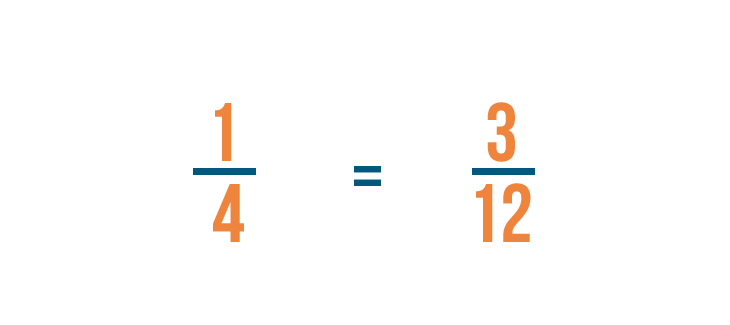
1/4 is equal to 3/12.
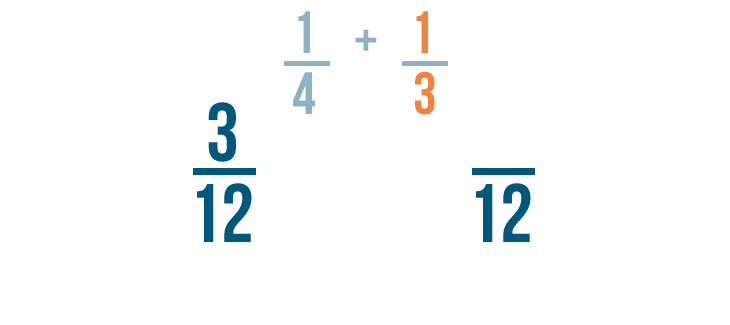
Now let's look at the fraction on the right: 1/3. We changed its denominator to 12 as well.
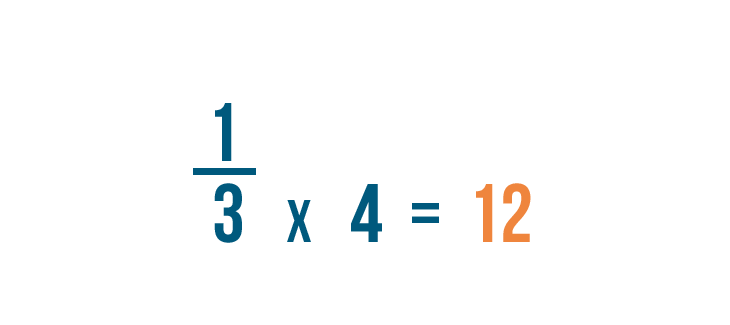
Our old denominator was 3. We multiplied it by 4 to get 12.
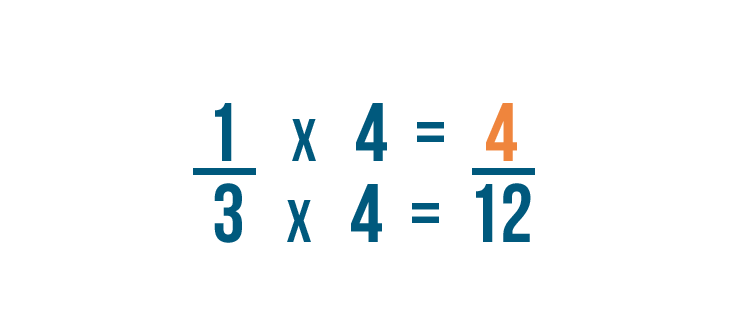
We'll also multiply the numerator by 4. 1 times 4 equals 4.
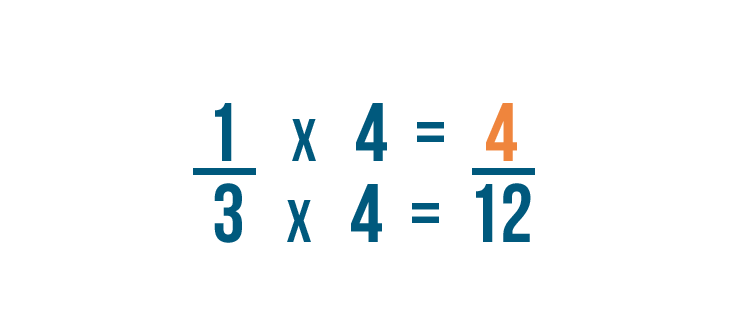
So 1/3 is equal to 4/12.
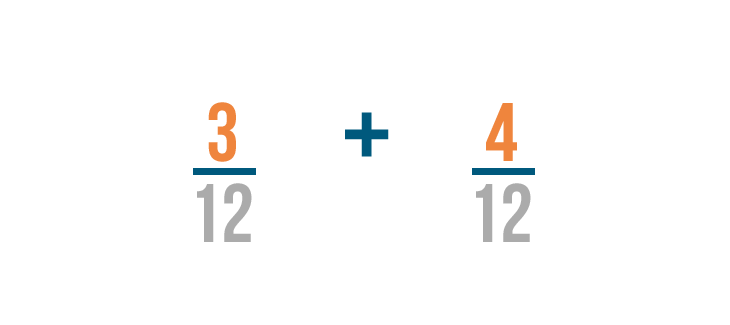
Now that our fractions have the same denominator, we can add them like we normally do.
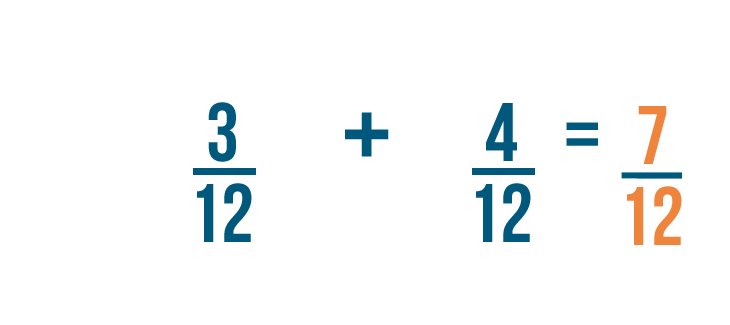
3 plus 4 equals 7. As usual, the denominator stays the same. So 3/12 plus 4/12 equals 7/12.

Try This!
Try solving the addition problems below.
Subtracting fractions with different denominators
We just saw that fractions can only be added when they have the same denominator. The same thing is true when we're subtracting fractions. Before we can subtract, we'll have to change our fractions so they have the same denominator.
Click through the slideshow to learn how to subtract fractions with different denominators.
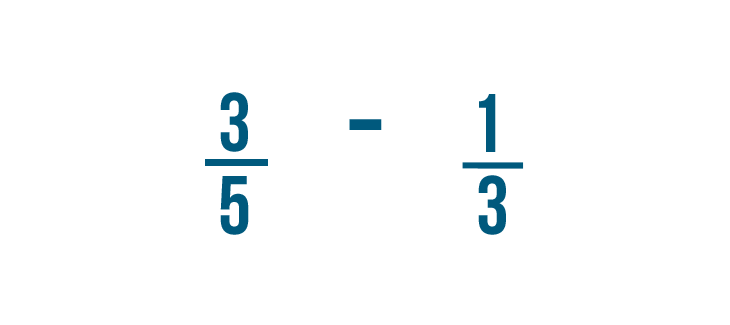
Let's try subtracting 1/3 from 3/5.
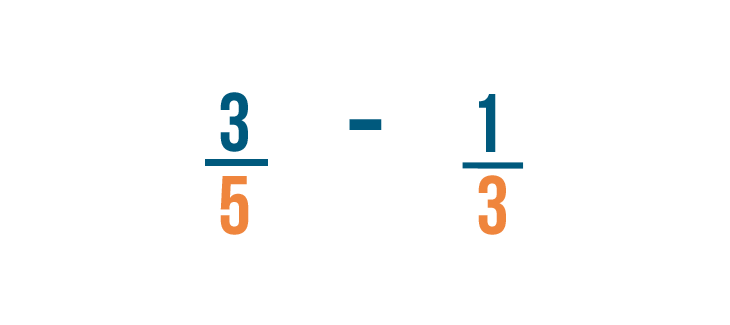
First, we'll change the denominators of both fractions to be the same by finding the lowest common denominator.
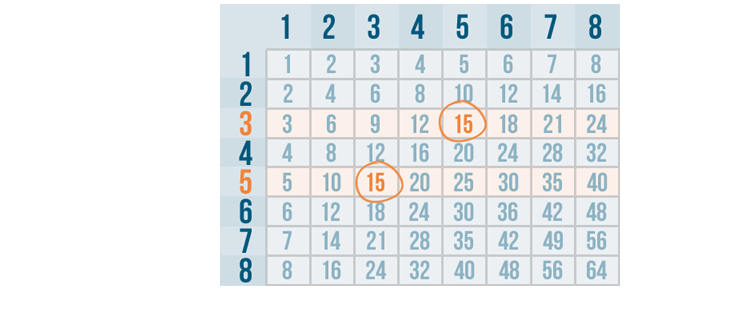
It looks like 15 is the smallest number that can be divided evenly by 3 and 5, so 15 is our LCD.
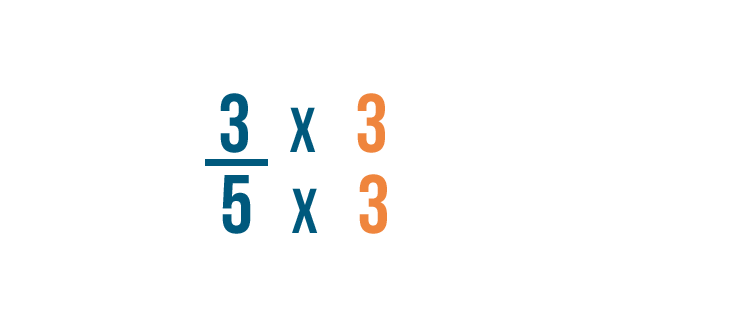
Now we'll change our first fraction. To change the denominator to 15, we'll multiply the denominator and the numerator by 3.
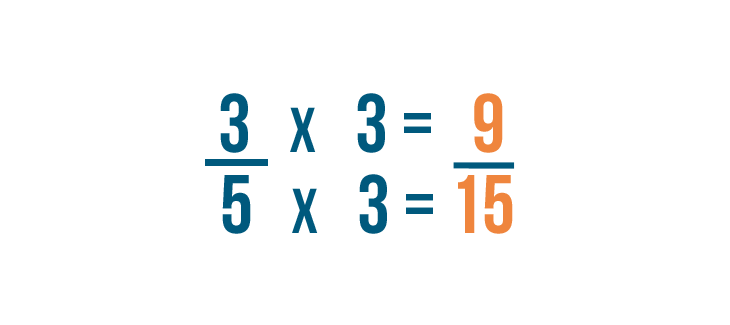
5 times 3 equals 15. So our fraction is now 9/15.
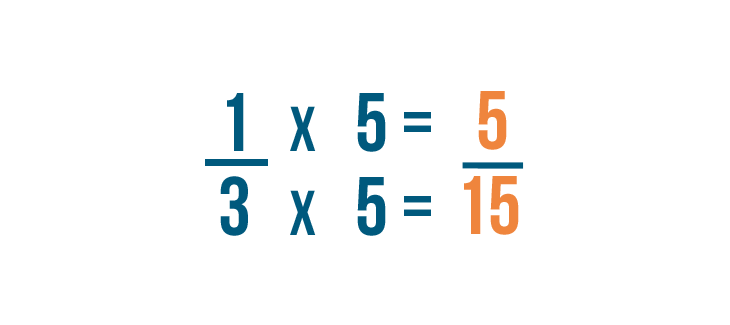
Now let's change the second fraction. To change the denominator to 15, we'll multiply both numbers by 5 to get 5/15.
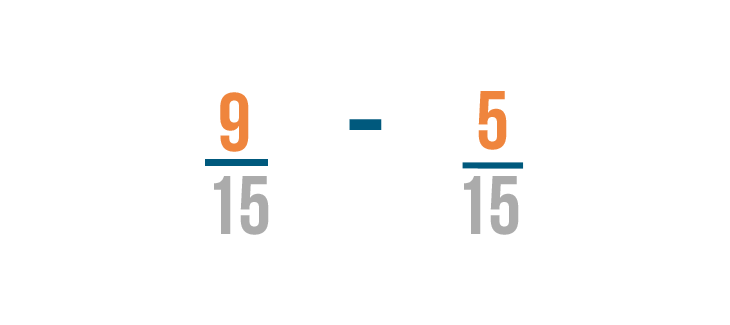
Now that our fractions have the same denominator, we can subtract like we normally do.
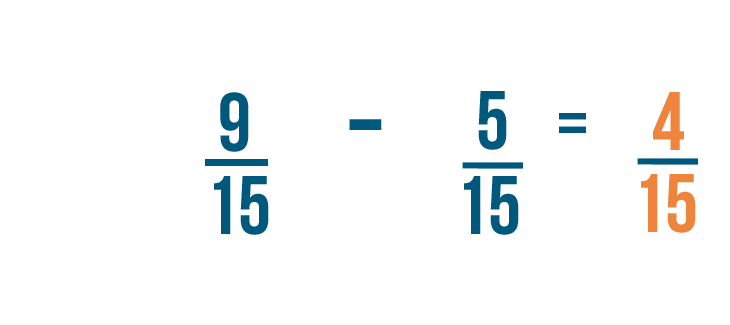
9 minus 5 equals 4. As always, the denominator stays the same. So 9/15 minus 5/15 equals 4/15.

Try This!
Try solving the subtraction problems below.
Adding and subtracting mixed numbers
Over the last few pages, you've practiced adding and subtracting different kinds of fractions. But some problems will need one extra step. For example, can you add the fractions below?
In Introduction to Fractions, you learned about mixed numbers. A mixed number has both a fraction and a whole number. An example is 2 1/2, or two-and-a-half. Another way to write this would be 5/2, or five-halves. These two numbers look different, but they're actually the same.
5/2 is an improper fraction. This just means the top number is larger than the bottom number. Even though improper fractions look strange, you can add and subtract them just like normal fractions. Mixed numbers aren't easy to add, so you'll have to convert them into improper fractions first.
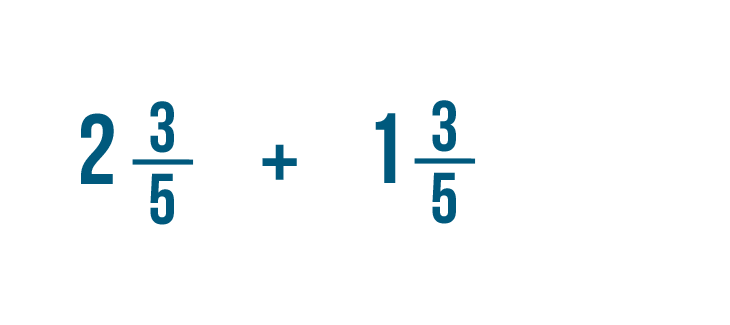
Let's add these two mixed numbers: 2 3/5 and 1 3/5.
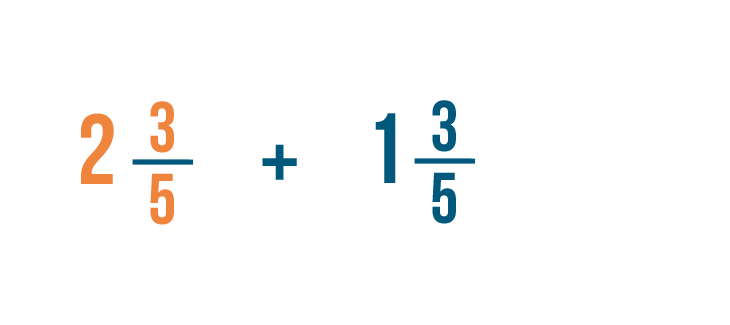
We'll need to convert these mixed numbers to improper fractions. Let's start with 2 3/5.
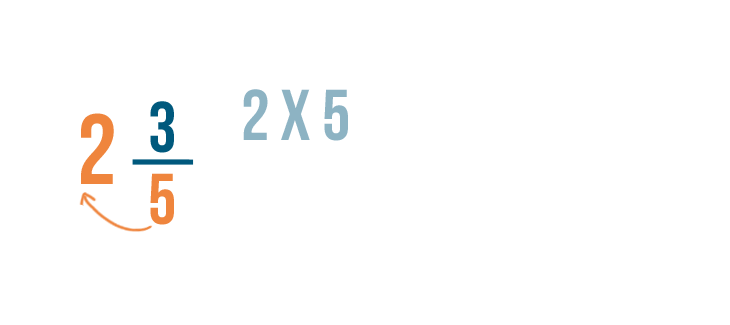
As you learned in Lesson 2, we'll multiply the whole number, 2, by the bottom number, 5.
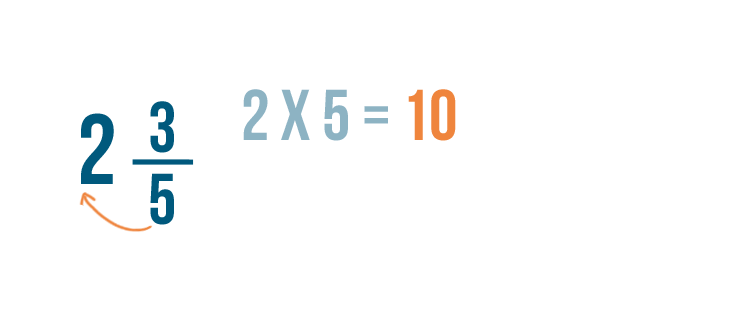
2 times 5 equals 10.
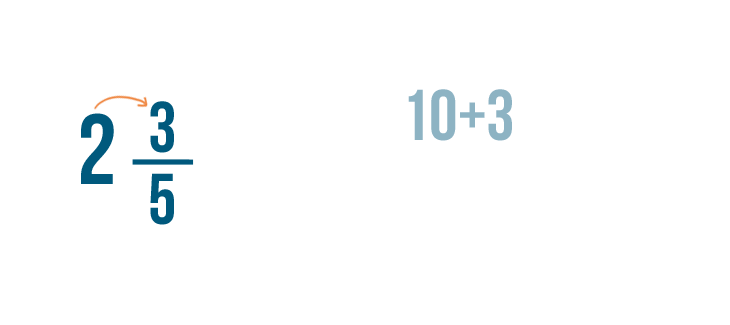
Now, let's add 10 to the numerator, 3.
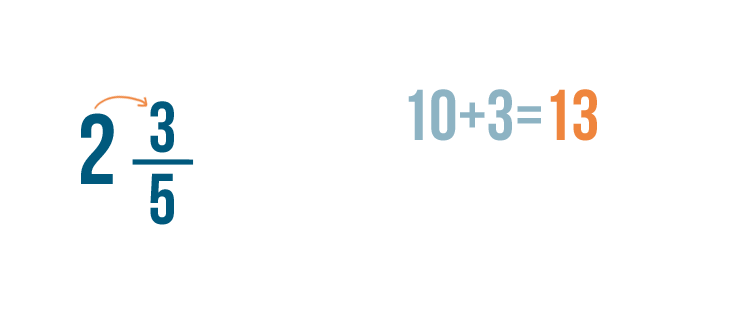
10 + 3 equals 13.
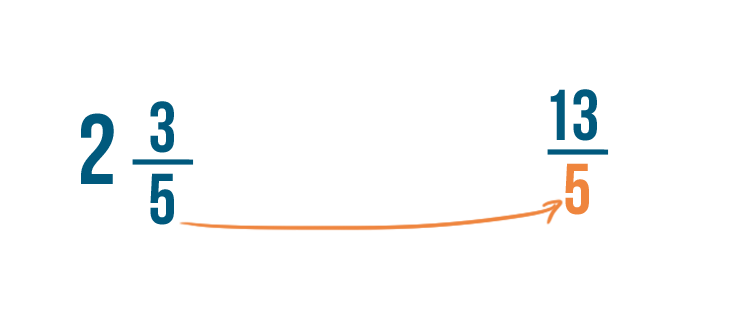
Just like when you add fractions, the denominator stays the same. Our improper fraction is 13/5.
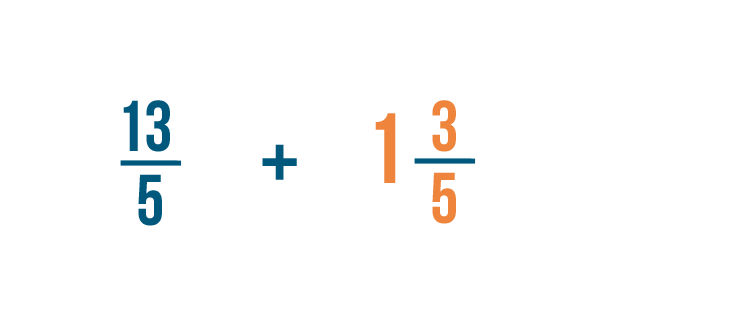
Now we'll need to convert our second mixed number: 1 3/5.
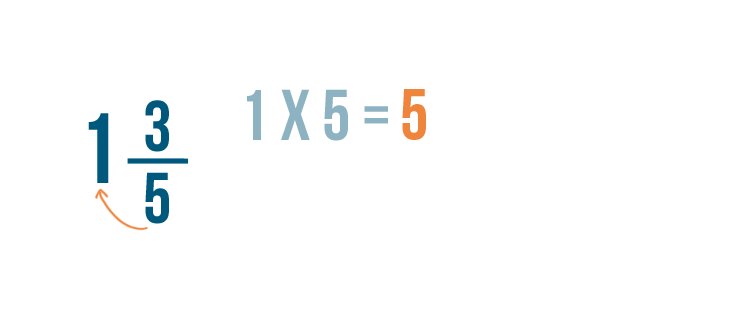
First, we'll multiply the whole number by the denominator. 1 x 5 = 5.
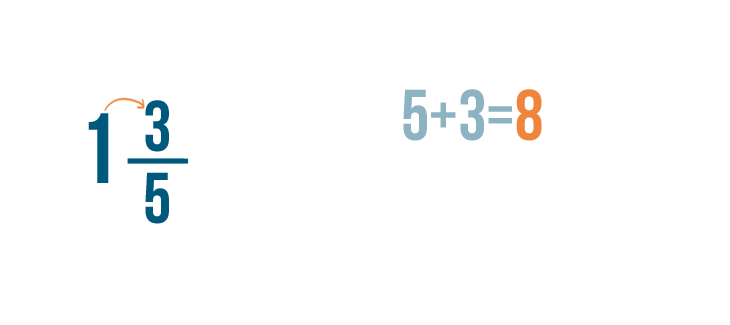
Next, we'll add 5 to the numerators. 5 + 3 = 8.

Just like last time, the denominator remains the same. So we've changed 1 3/5 to 8/5.
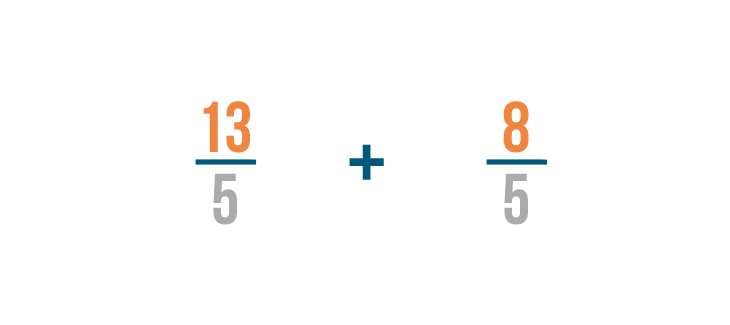
Now that we've changed our mixed numbers to improper fractions, we can add like we normally do.
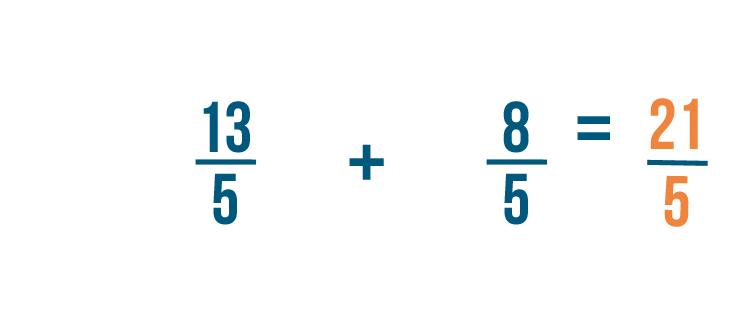
13 plus 8 equals 21. As usual, the denominator will stay the same. So 13/5 + 8/5 = 21/5.
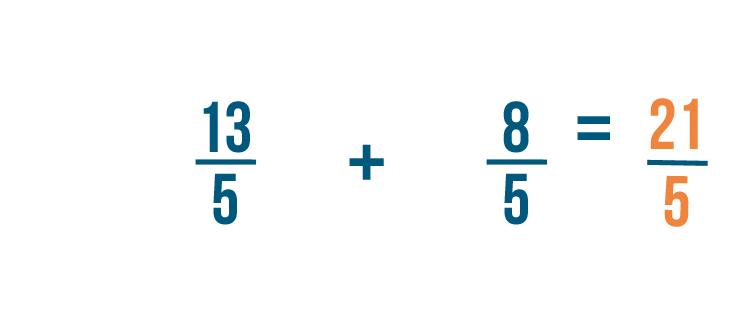
Because we started with a mixed number, let's convert this improper fraction back into a mixed number.
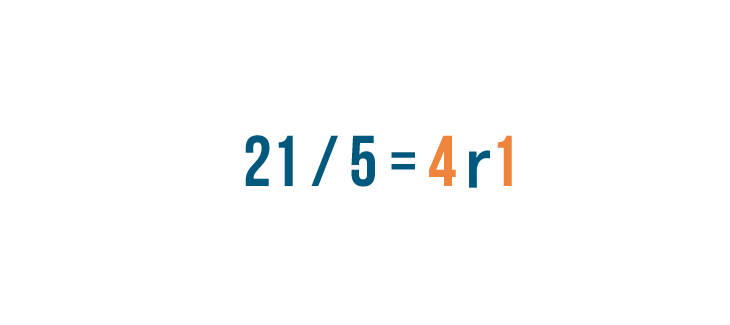
As you learned in the previous lesson, divide the top number by the bottom number. 21 divided by 5 equals 4, with a remainder of 1.
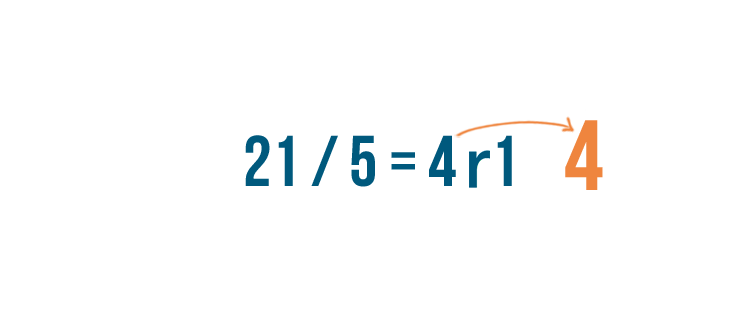
The answer, 4, will become our whole number.
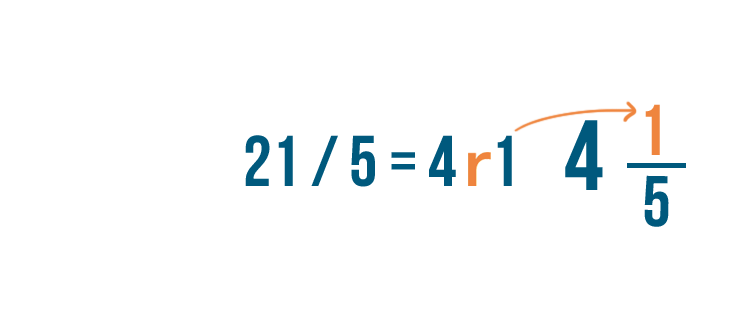
And the remainder, 1, will become the numerator of the fraction.
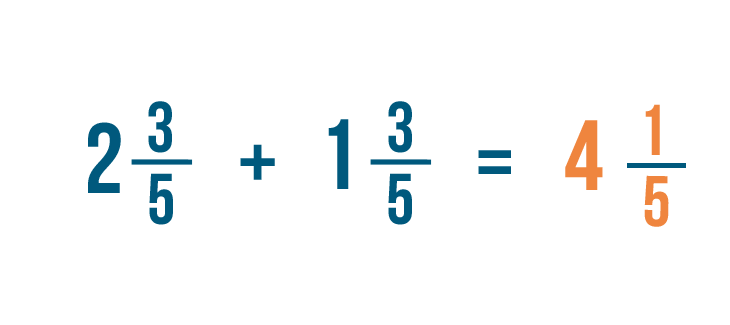
So 2 3/5 + 1 3/5 = 4 1/5.

/en/fractions/multiplying-and-dividing-fractions/content/