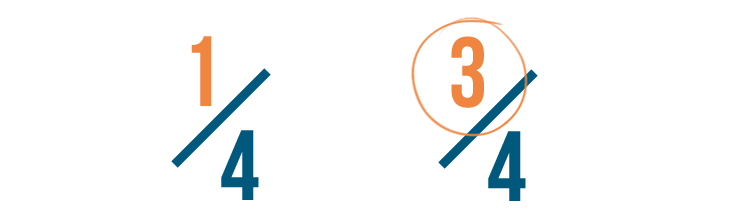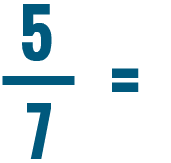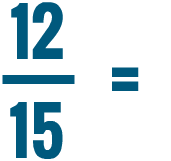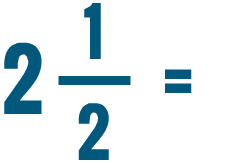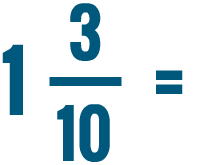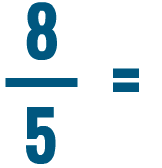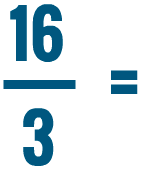Lesson 2: Comparing and Reducing Fractions
/en/fractions/introduction-to-fractions/content/
Comparing fractions
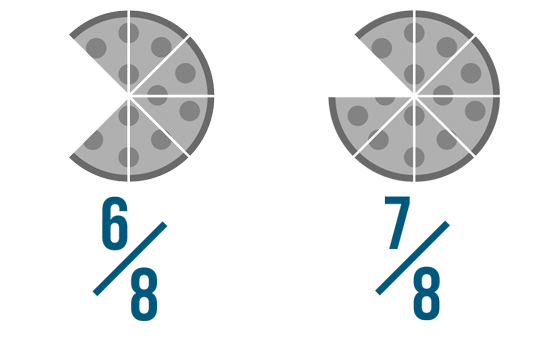
In Introduction to Fractions, we learned that fractions are a way of showing part of something. Fractions are useful, since they let us tell exactly how much we have of something. Some fractions are larger than others. For example, which is larger: 6/8 of a pizza or 7/8 of a pizza?
In this image, we can see that 7/8 is larger. The illustration makes it easy to compare these fractions. But how could we have done it without the pictures?
Click through the slideshow to learn how to compare fractions.
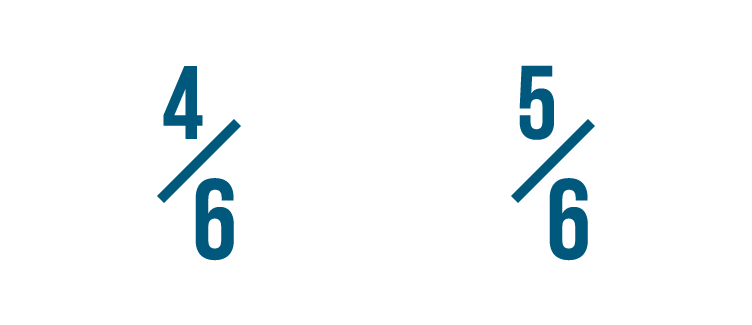
Earlier, we saw that fractions have two parts.
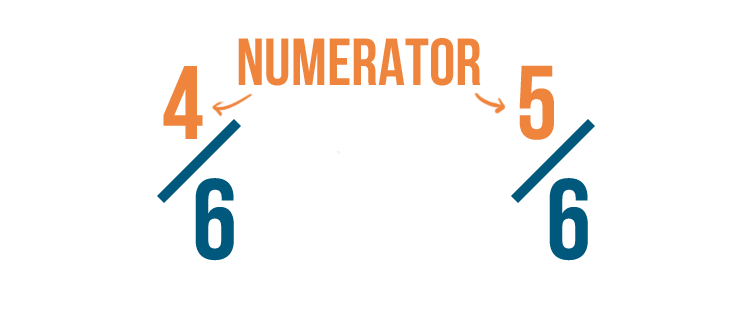
One part is the top number, or numerator.

The other is the bottom number, or denominator.

The denominator tells us how many parts are in a whole.

The numerator tells us how many of those parts we have.

When fractions have the same denominator, it means they're split into the same number of parts.

This means we can compare these fractions just by looking at the numerator.

Here, 5 is more than 4...

Here, 5 is more than 4...so we can tell that 5/6 is more than 4/6.
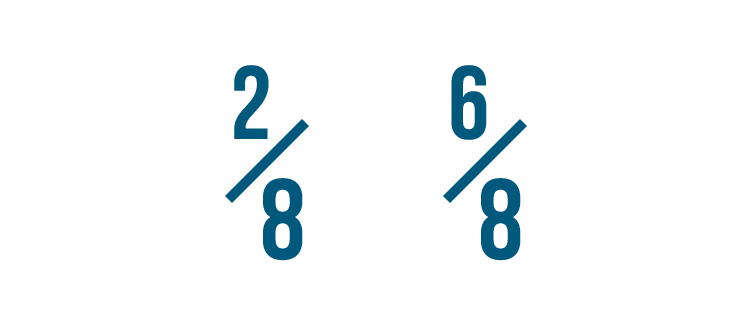
Let's look at another example. Which of these is larger: 2/8 or 6/8?
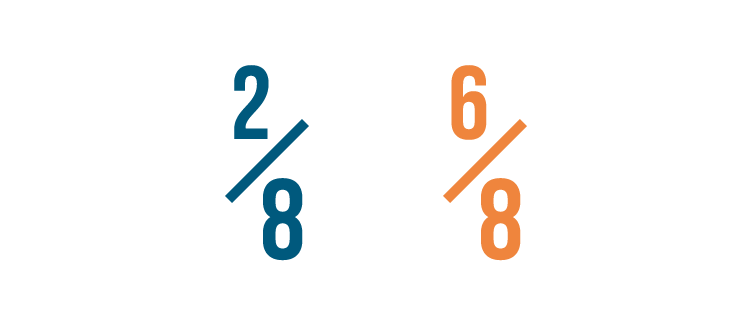
If you thought 6/8 was larger, you were right!
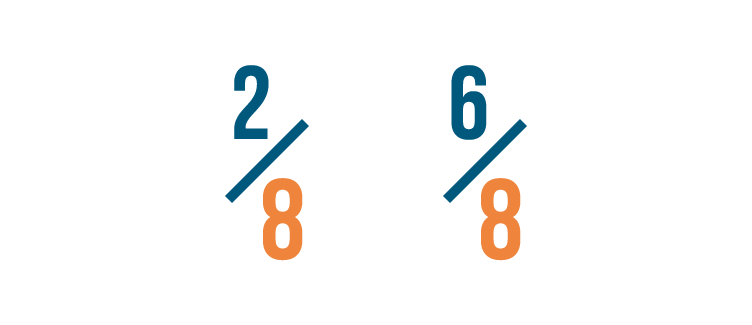
Both fractions have the same denominator.
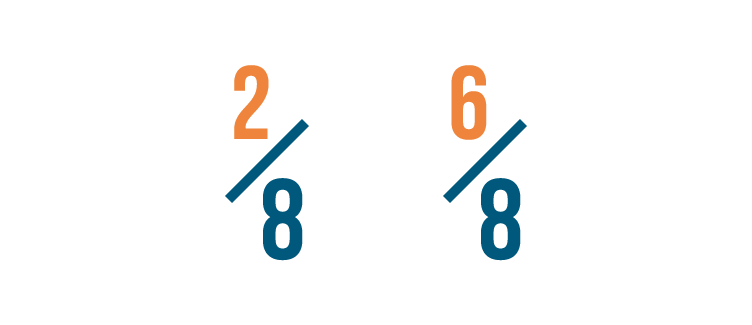
So we compared the numerators. 6 is larger than 2, so 6/8 is more than 2/8.

As you saw, if two or more fractions have the same denominator, you can compare them by looking at their numerators. As you can see below, 3/4 is larger than 1/4. The larger the numerator, the larger the fraction.
Comparing fractions with different denominators
On the previous page, we compared fractions that have the same bottom numbers, or denominators. But you know that fractions can have any number as a denominator. What happens when you need to compare fractions with different bottom numbers?
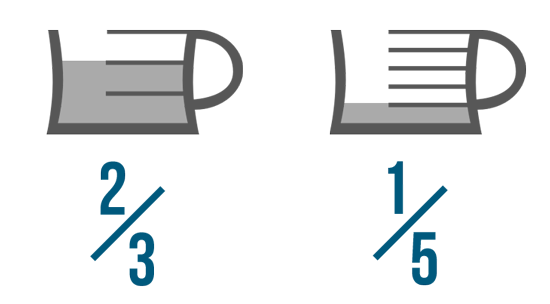
For example, which of these is larger: 2/3 or 1/5? It's difficult to tell just by looking at them. After all, 2 is larger than 1, but the denominators aren't the same.
If you look at the picture, though, the difference is clear: 2/3 is larger than 1/5. With an illustration, it was easy to compare these fractions, but how could we have done it without the picture?
Click through the slideshow to learn how to compare fractions with different denominators.
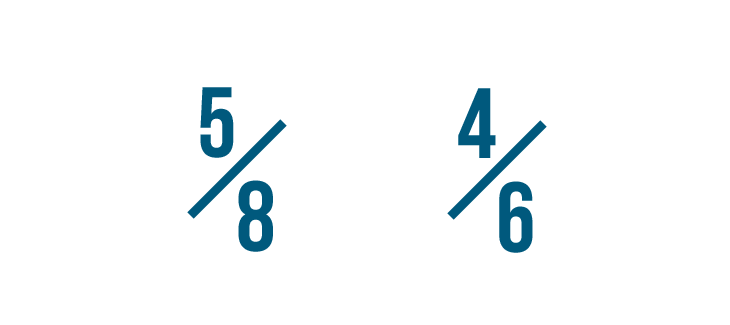
Let's compare these fractions: 5/8 and 4/6.
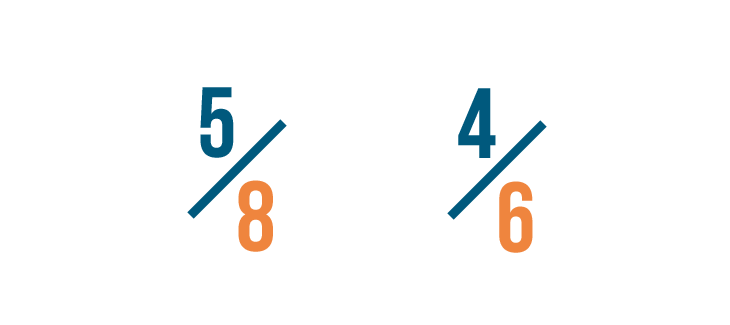
Before we compare them, we need to change both fractions so they have the same denominator, or bottom number.
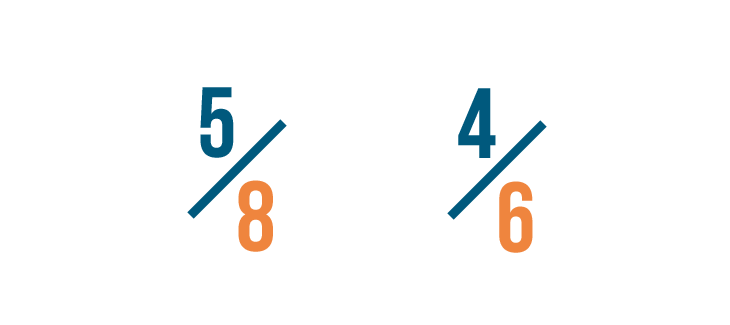
First, we'll find the smallest number that can be divided by both denominators. We call that the lowest common denominator.
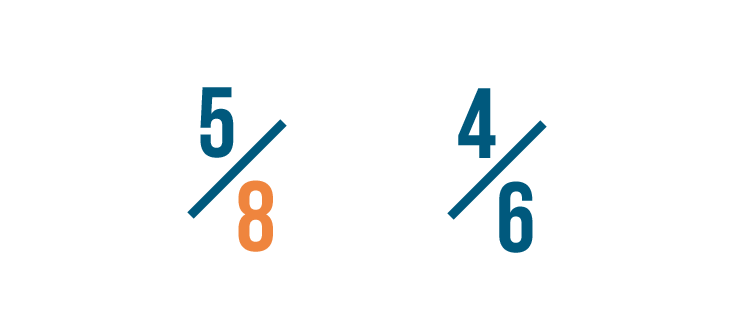
Our first step is to find numbers that can be divided evenly by 8.

Using a multiplication table makes this easy. All of the numbers on the 8 row can be divided evenly by 8.
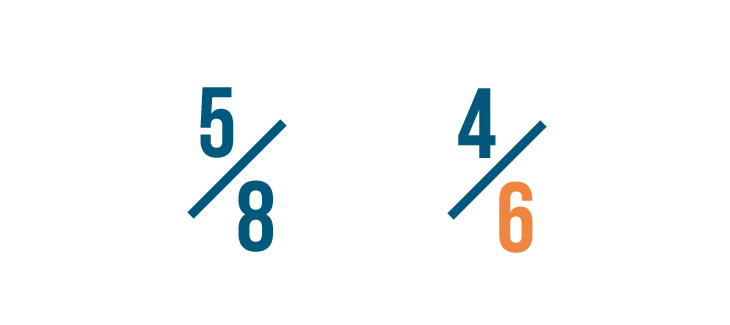
Now let's look at our second denominator: 6.

We can use the multiplication table again. All of the numbers in the 6 row can be divided evenly by 6.
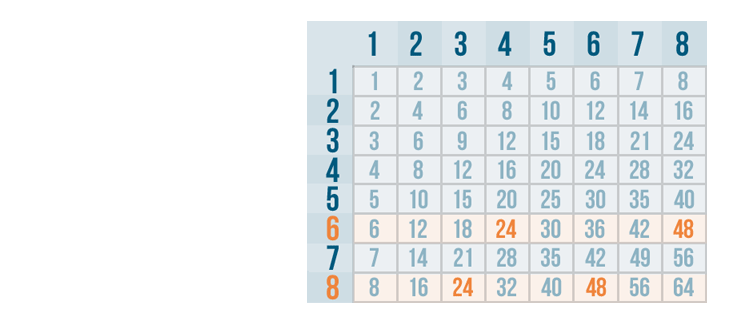
Let's compare the two rows. It looks like there are a few numbers that can be divided evenly by both 6 and 8.
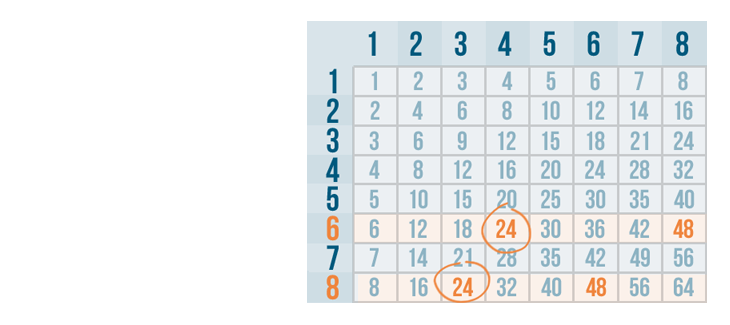
24 is the smallest number that appears on both rows, so it's the lowest common denominator.
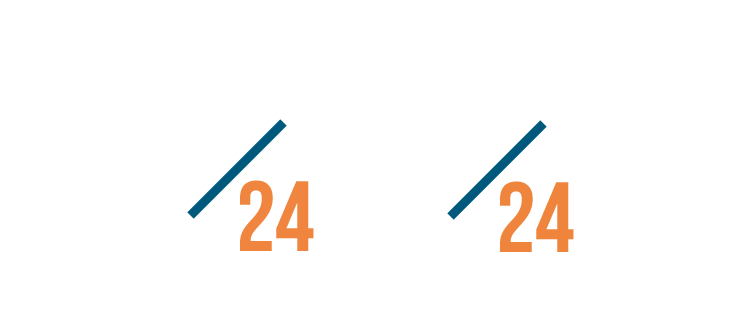
Now we're going to change our fractions so they both have the same denominator: 24.
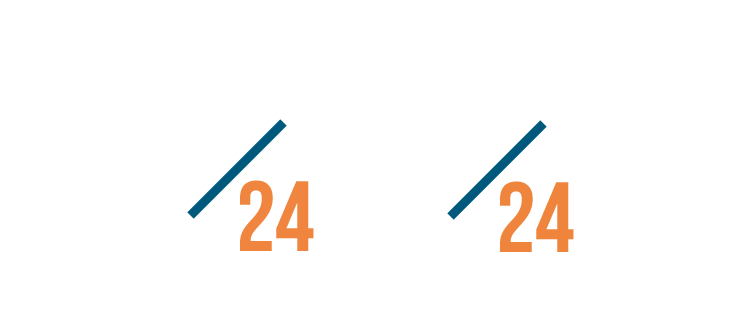
To do that, we'll have to change the numerators the same way we changed the denominators.
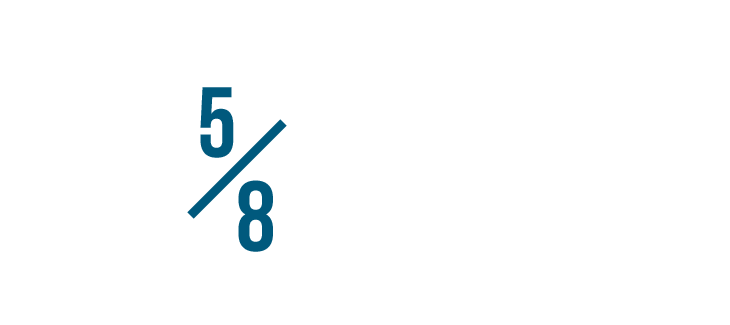
Let’s look at 5/8 again. In order to change the denominator to 24...
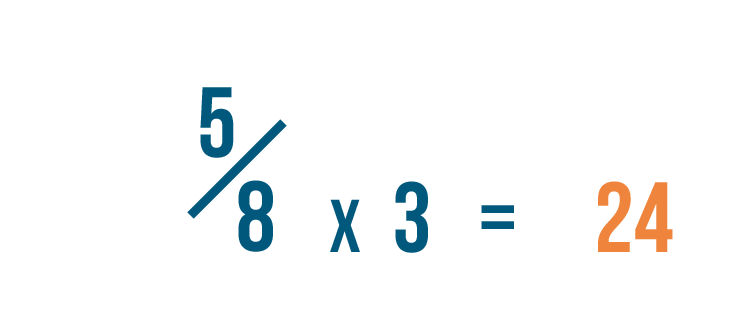
Let’s look at 5/8 again. In order to change the denominator to 24...we had to multiply 8 by 3.
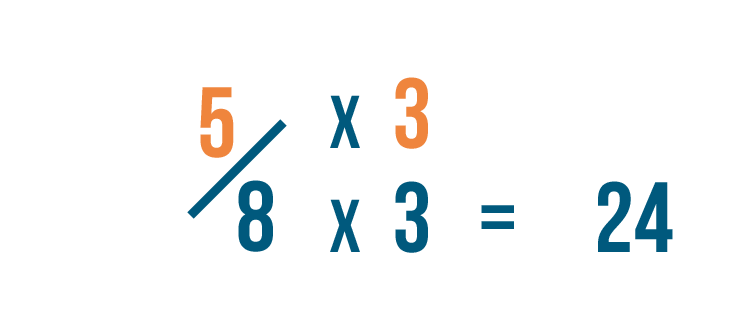
Since we multiplied the denominator by 3, we'll also multiply the numerator, or top number, by 3.
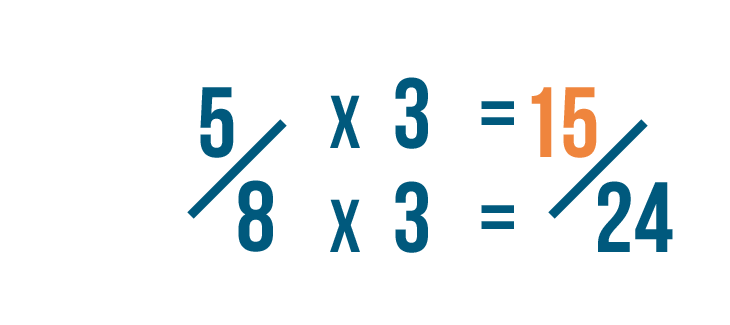
5 times 3 equals 15. So we've changed 5/8 into 15/24.
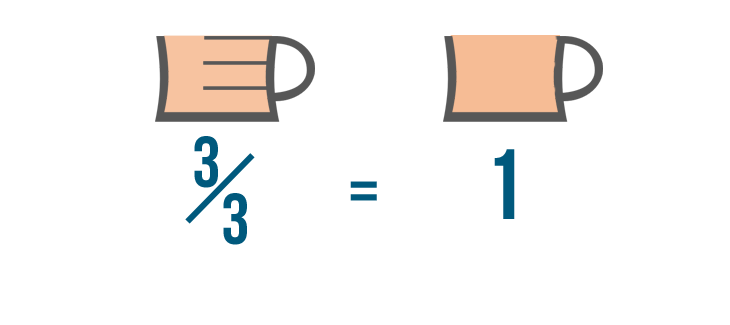
We can do that because any number over itself is equal to 1.
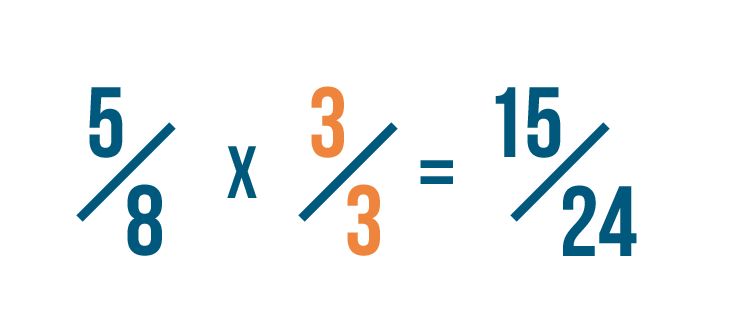
So when we multiply 5/8 by 3/3...
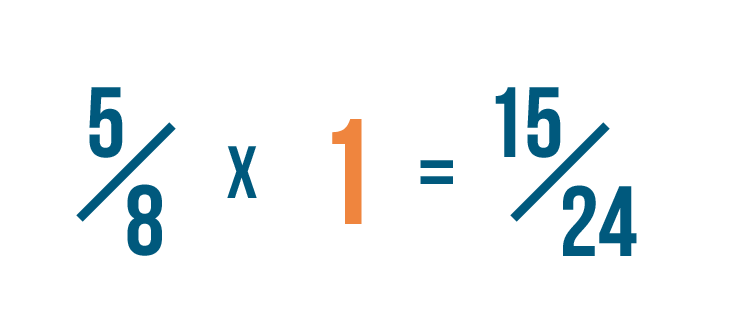
So when we multiply 5/8 by 3/3...we're really multiplying 5/8 by 1.
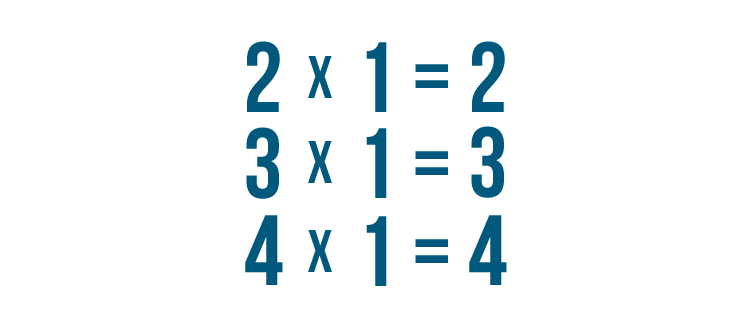
Since any number times 1 is equal to itself...
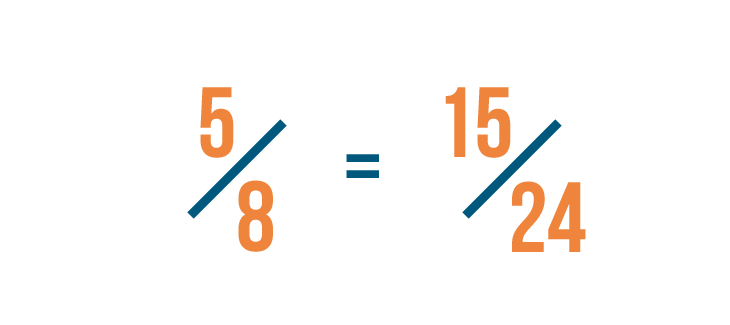
Since any number times 1 is equal to itself...we can say that 5/8 is equal to 15/24.
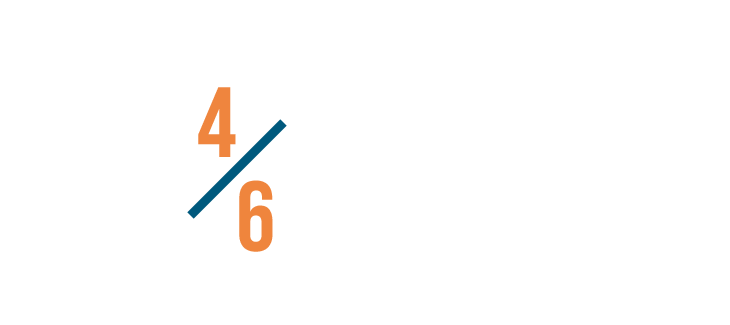
Now we'll do the same to our other fraction: 4/6. We also changed its denominator to 24.
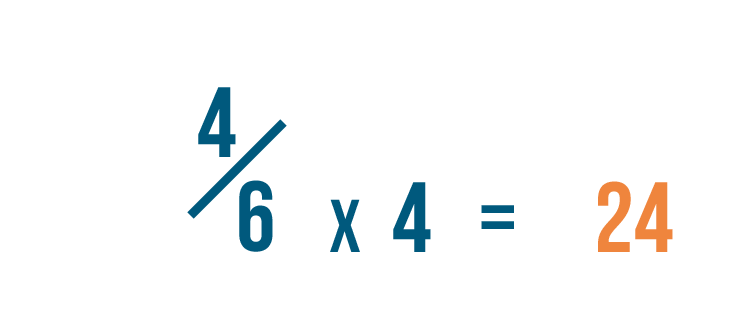
Our old denominator was 6. To get 24, we multiplied 6 by 4.
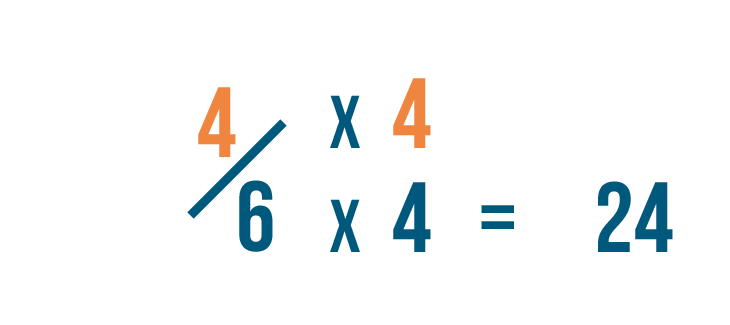
So we'll also multiply the numerator by 4.
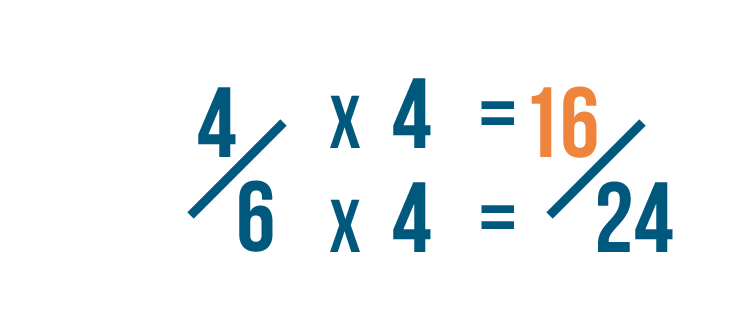
4 times 4 is 16. So 4/6 is equal to 16/24.
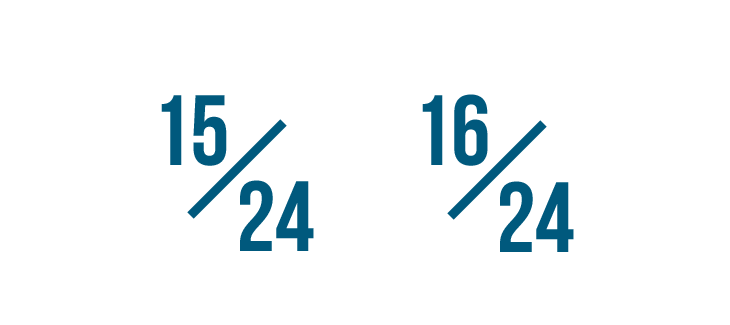
Now that the denominators are the same, we can compare the two fractions by looking at their numerators.
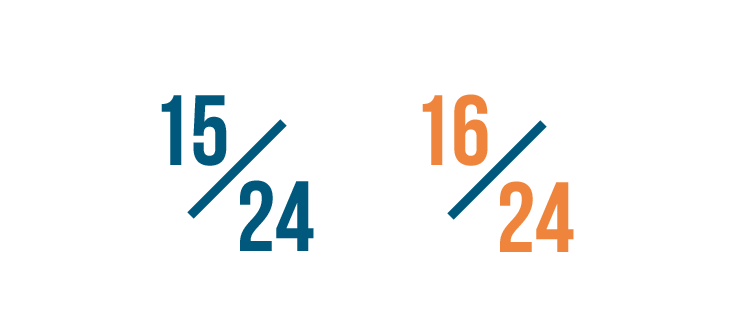
16/24 is larger than 15/24...
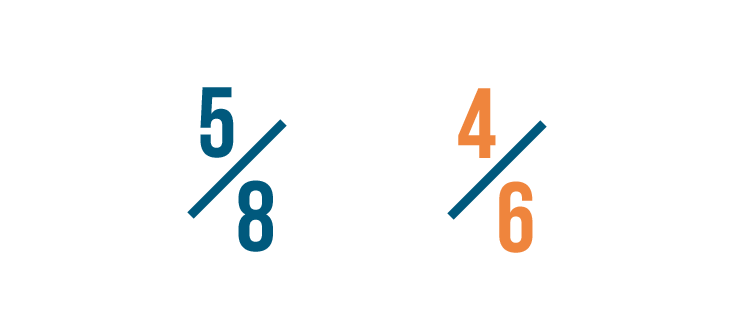
16/24 is larger than 15/24... so 4/6 is larger than 5/8.

Reducing fractions
Which of these is larger: 4/8 or 1/2?
If you did the math or even just looked at the picture, you might have been able to tell that they're equal. In other words, 4/8 and 1/2 mean the same thing, even though they're written differently.
If 4/8 means the same thing as 1/2, why not just call it that? One-half is easier to say than four-eighths, and for most people it's also easier to understand. After all, when you eat out with a friend, you split the bill in half, not in eighths.
If you write 4/8 as 1/2, you're reducing it. When we reduce a fraction, we're writing it in a simpler form. Reduced fractions are always equal to the original fraction.
We already reduced 4/8 to 1/2. If you look at the examples below, you can see that other numbers can be reduced to 1/2 as well. These fractions are all equal.
5/10 = 1/2
11/22 = 1/2
36/72 = 1/2
These fractions have all been reduced to a simpler form as well.
4/12 = 1/3
14/21 = 2/3
35/50 = 7/10
Click through the slideshow to learn how to reduce fractions by dividing.

Let's try reducing this fraction: 16/20.
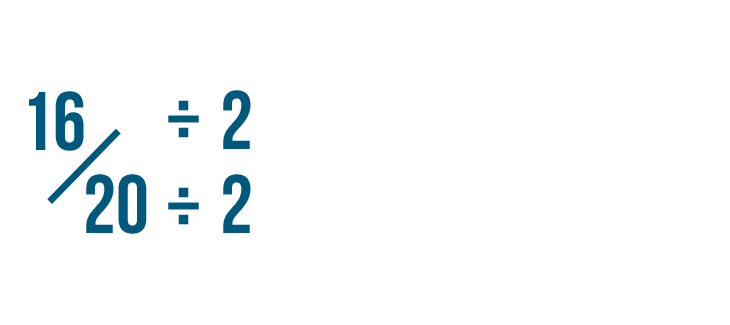
Since the numerator and denominator are even numbers, you can divide them by 2 to reduce the fraction.
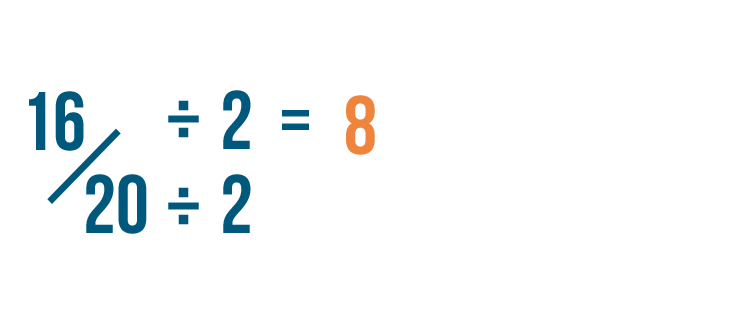
First, we'll divide the numerator by 2. 16 divided by 2 is 8.
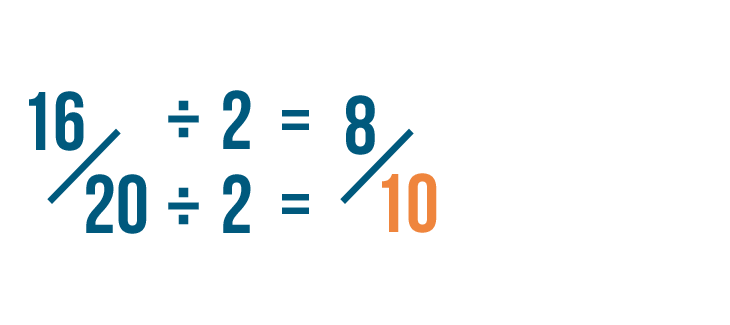
Next, we'll divide the denominator by 2. 20 divided by 2 is 10.
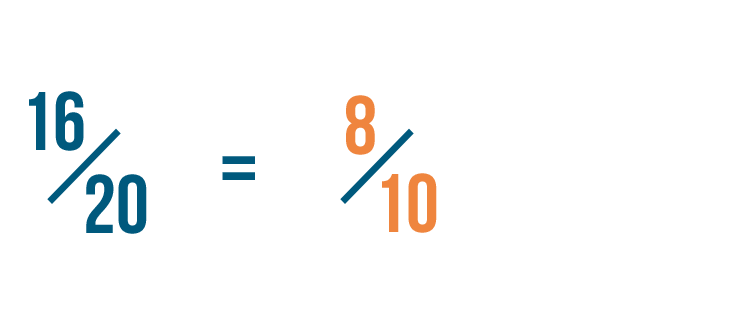
We've reduced 16/20 to 8/10. We could also say that 16/20 is equal to 8/10.
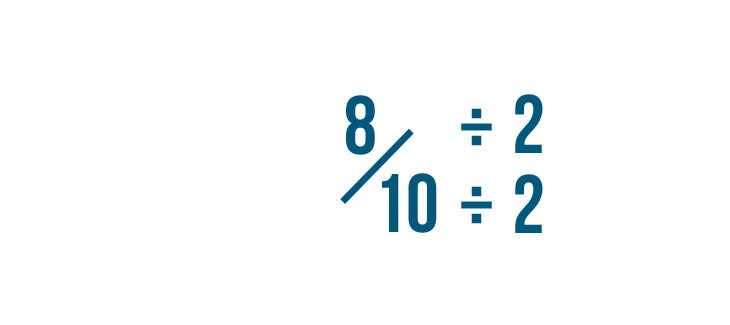
If the numerator and denominator can still be divided by 2, we can continue reducing the fraction.
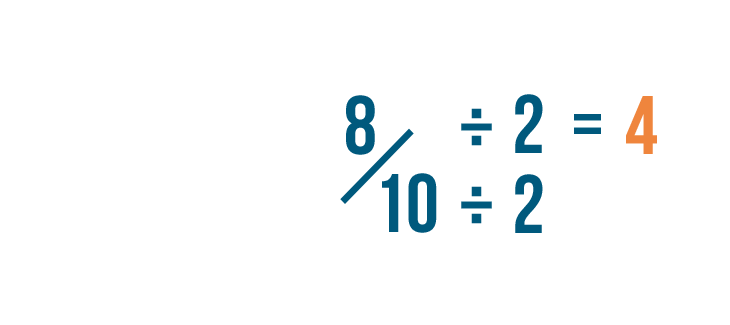
8 divided by 2 is 4.
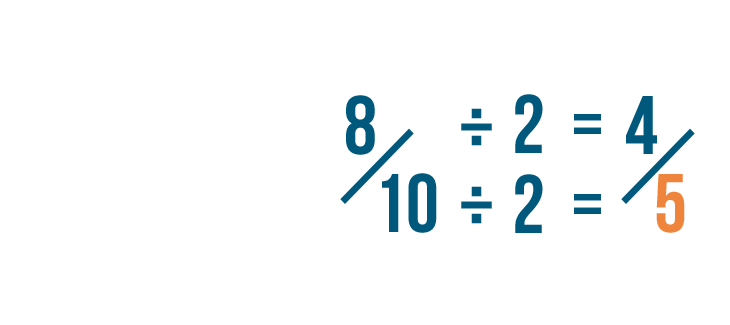
10 divided by 2 is 5.

Since there's no number that 4 and 5 can be divided by, we can't reduce 4/5 any further.
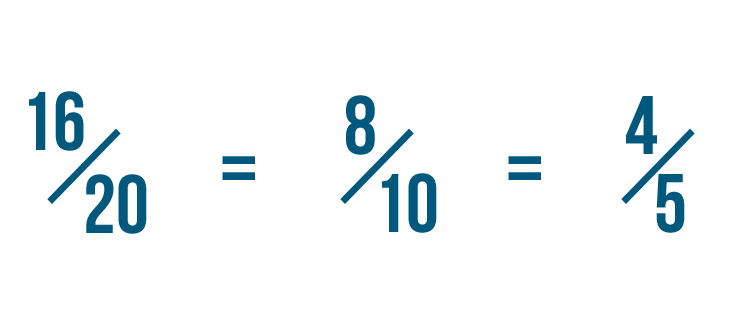
This means 4/5 is the simplest form of 16/20.

Let's try reducing another fraction: 6/9.

While the numerator is even, the denominator is an odd number, so we can't reduce by dividing by 2.
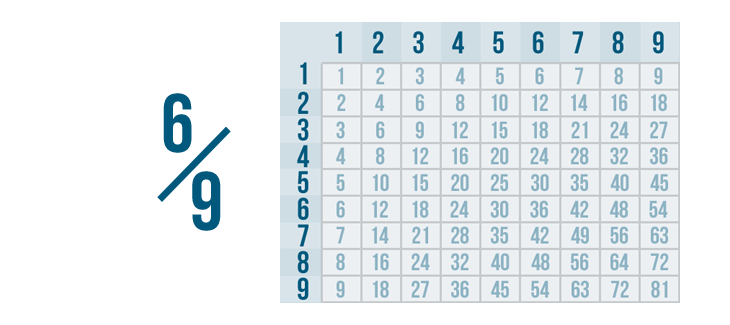
Instead, we'll need to find a number that 6 and 9 can be divided by. A multiplication table will make that number easy to find.
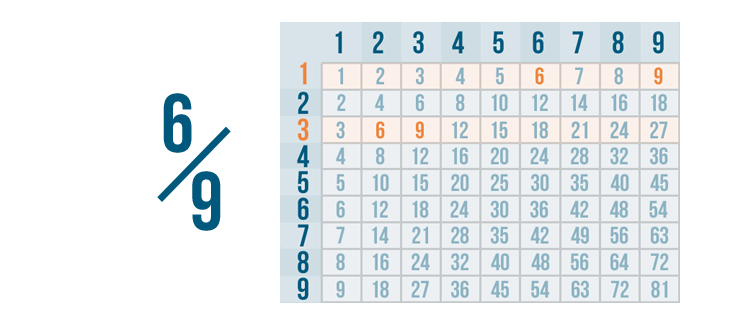
Let's find 6 and 9 on the same row. As you can see, 6 and 9 can both be divided by 1 and 3.

Dividing by 1 won't change these fractions, so we'll use the largest number that 6 and 9 can be divided by.
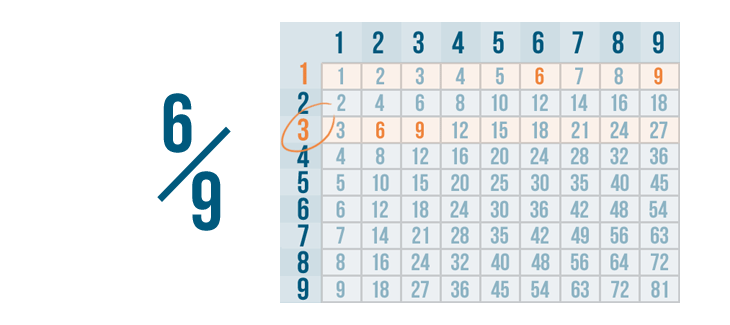
That's 3. This is called the greatest common divisor, or GCD. (You can also call it the greatest common factor, or GCF.)

3 is the GCD of 6 and 9 because it's the largest number they can be divided by.
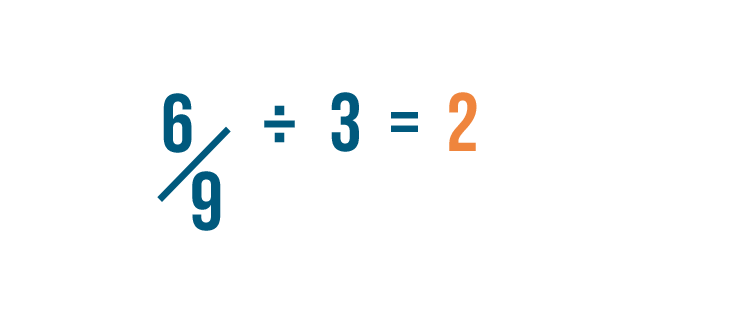
So we'll divide the numerator by 3. 6 divided by 3 is 2.
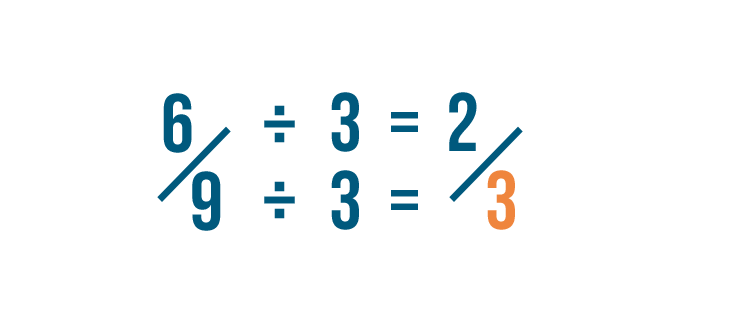
Then we'll divide the denominator by 3. 9 divided by 3 is 3.
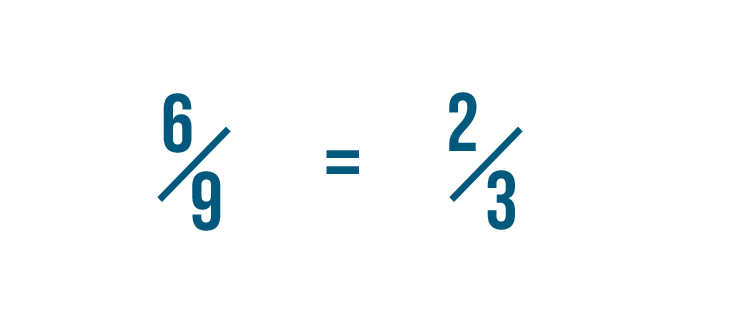
Now we've reduced 6/9 to 2/3, which is its simplest form. We could also say that 6/9 is equal to 2/3.

Irreducible fractions
Not all fractions can be reduced. Some are already as simple as they can be. For example, you can't reduce 1/2 because there's no number other than 1 that both 1 and 2 can be divided by. (For that reason, you can't reduce any fraction that has a numerator of 1.)
Some fractions that have larger numbers can't be reduced either. For instance, 17/36 can't be reduced because there's no number that both 17 and 36 can be divided by. If you can't find any common multiples for the numbers in a fraction, chances are it's irreducible.
Try This!
Reduce each fraction to its simplest form.
Mixed numbers and improper fractions
In the previous lesson, you learned about mixed numbers. A mixed number has both a fraction and a whole number. An example is 1 2/3. You'd read 1 2/3 like this: one and two-thirds.
Another way to write this would be 5/3, or five-thirds. These two numbers look different, but they're actually the same. 5/3 is an improper fraction. This just means the numerator is larger than the denominator.
There are times when you may prefer to use an improper fraction instead of a mixed number. It's easy to change a mixed number into an improper fraction. Let's learn how:
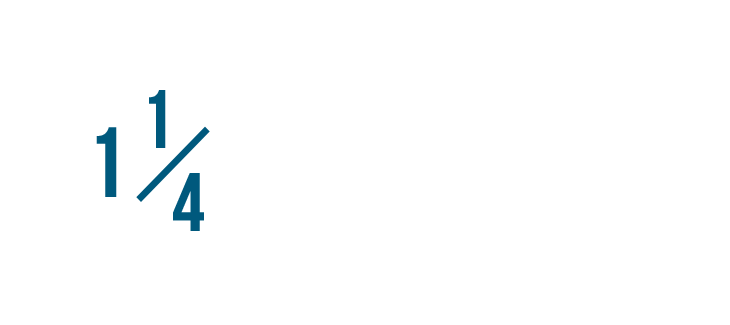
Let's convert 1 1/4 into an improper fraction.
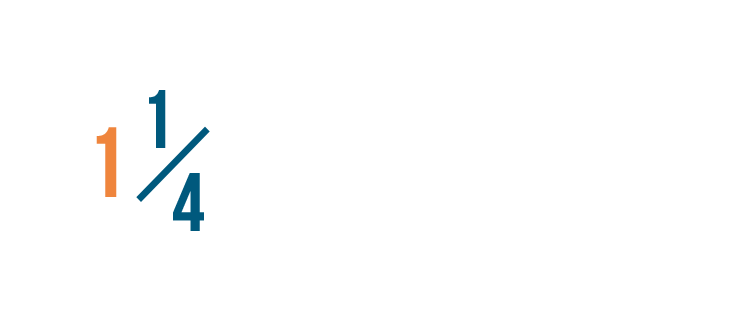
First, we'll need to find out how many parts make up the whole number: 1 in this example.
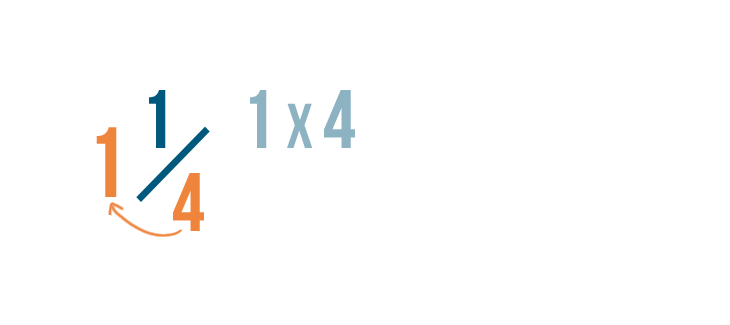
To do this, we'll multiply the whole number, 1, by the denominator, 4.
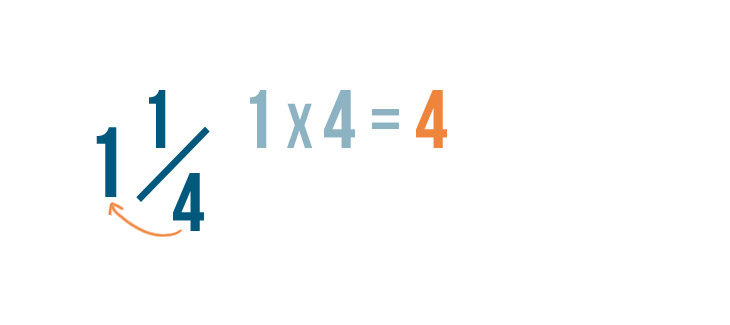
1 times 4 equals 4.
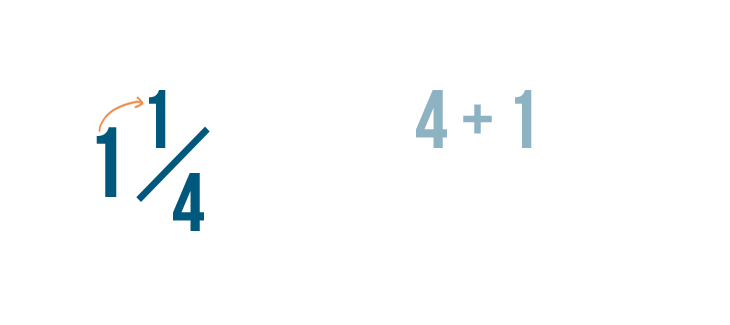
Now, let's add that number, 4, to the numerator, 1.
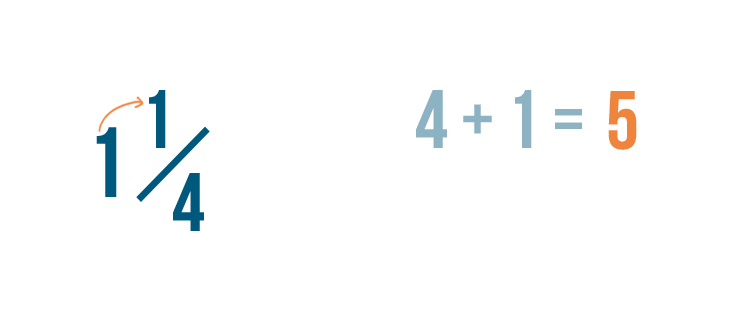
4 plus 1 equals 5.

The denominator stays the same.
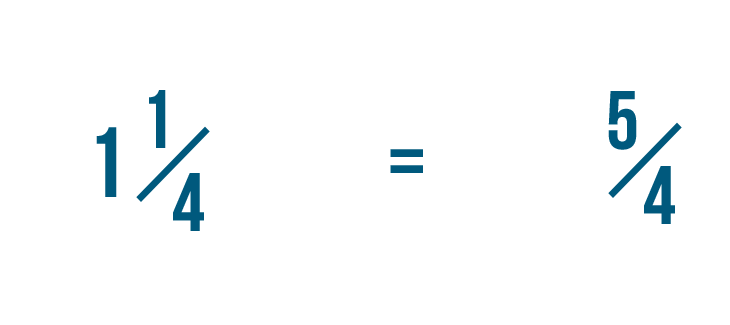
Our improper fraction is 5/4, or five-fourths. So we could say that 1 1/4 is equal to 5/4.
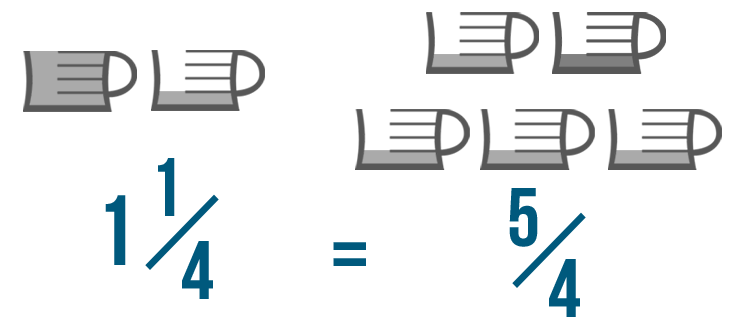
This means there are five 1/4s in 1 1/4.

Let's convert another mixed number: 2 2/5.
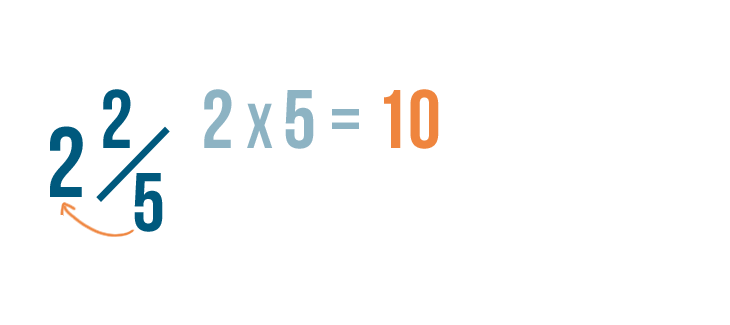
First, we'll multiply the whole number by the denominator. 2 times 5 equals 10.
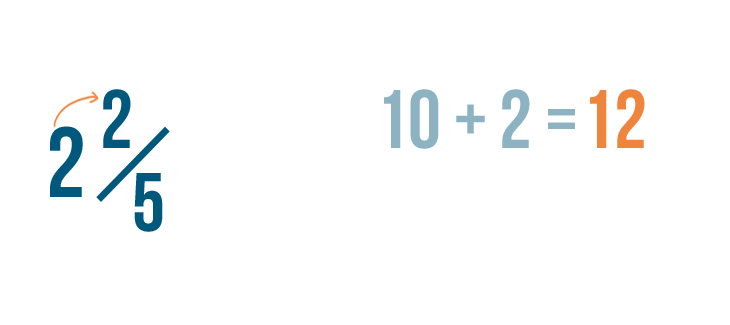
Next, we'll add 10 to the numerator. 10 plus 2 equals 12.

As always, the denominator will stay the same.
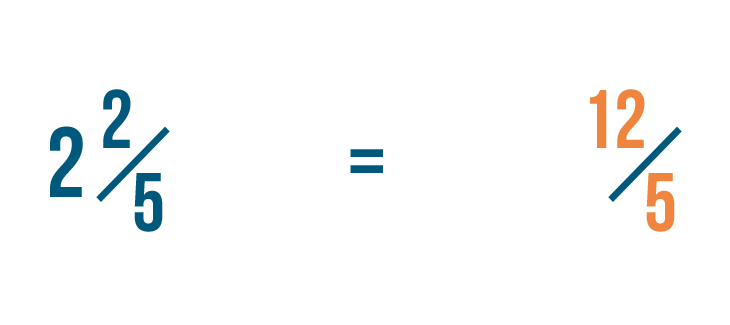
So 2 2/5 is equal to 12/5.

Try This!
Try converting these mixed numbers into improper fractions.
Converting improper fractions into mixed numbers
Improper fractions are useful for math problems that use fractions, as you'll learn later. However, they're also more difficult to read and understand than mixed numbers. For example, it's a lot easier to picture 2 4/7 in your head than 18/7.
Click through the slideshow to learn how to change an improper fraction into a mixed number.

Let's turn 10/4 into a mixed number.
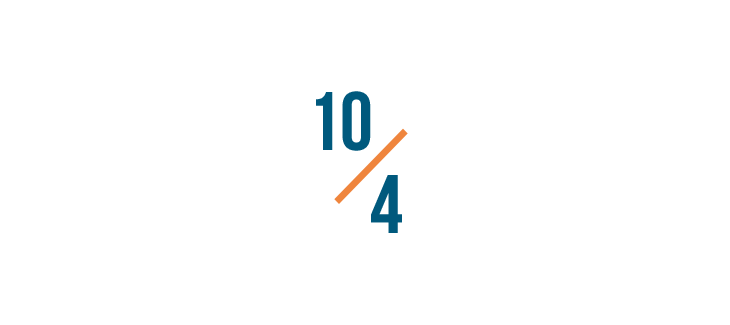
You can think of any fraction as a division problem. Just treat the line between the numbers like a division sign (/).

So we'll divide the numerator, 10, by the denominator, 4.
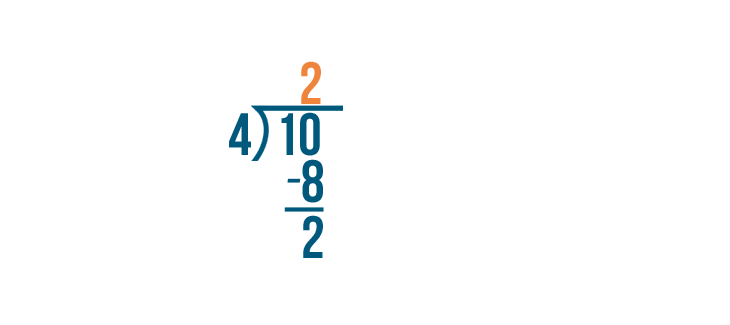
10 divided by 4 equals 2...
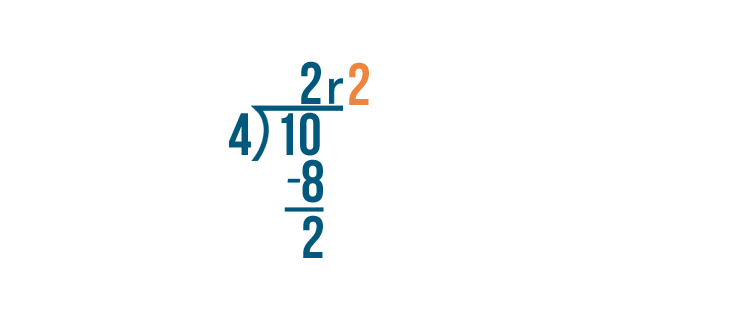
10 divided by 4 equals 2... with a remainder of 2.
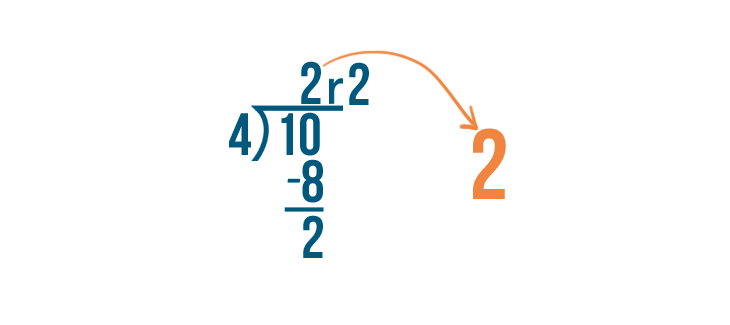
The answer, 2, will become our whole number because 10 can be divided by 4 twice.
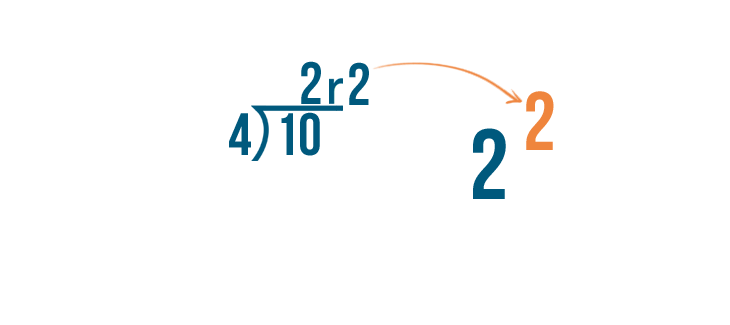
And the remainder, 2, will become the numerator of the fraction because we have 2 parts left over.
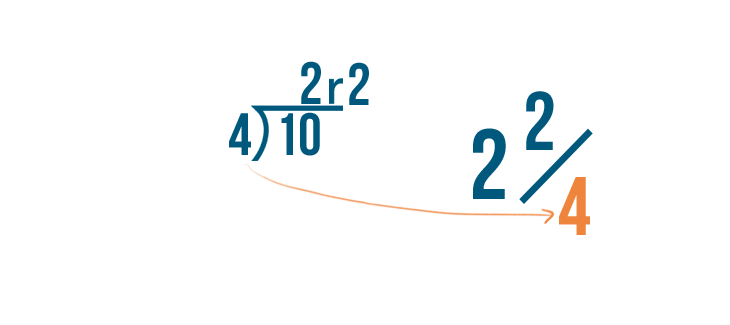
The denominator remains the same.
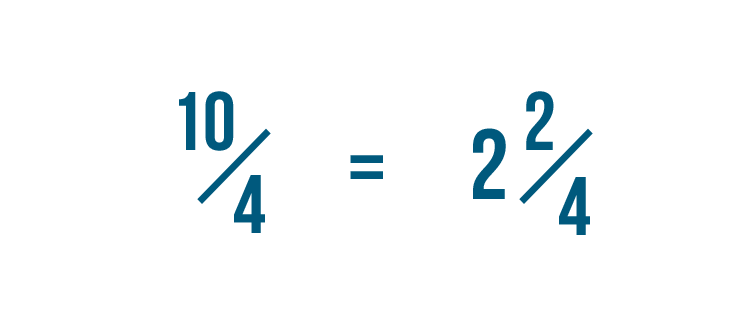
So 10/4 equals 2 2/4.
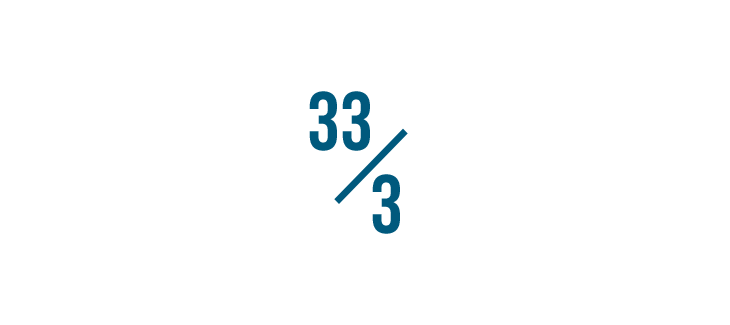
Let's try another example: 33/3.
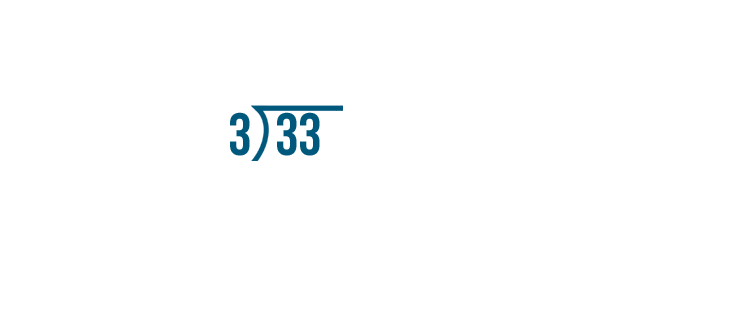
We'll divide the numerator, 33, by the denominator, 3.
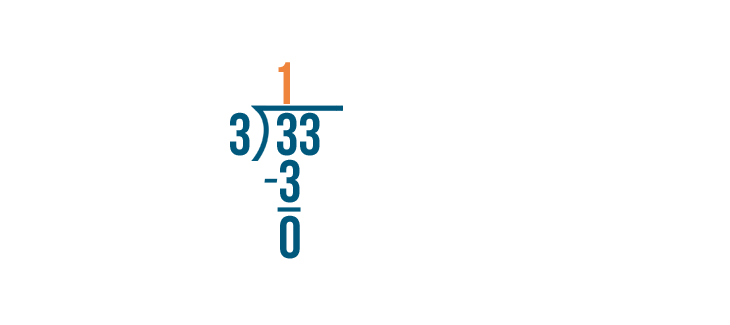
33 divided by 3...
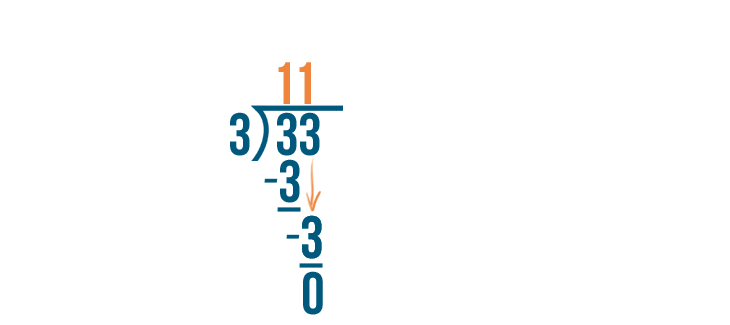
33 divided by 3... equals 11, with no remainder.
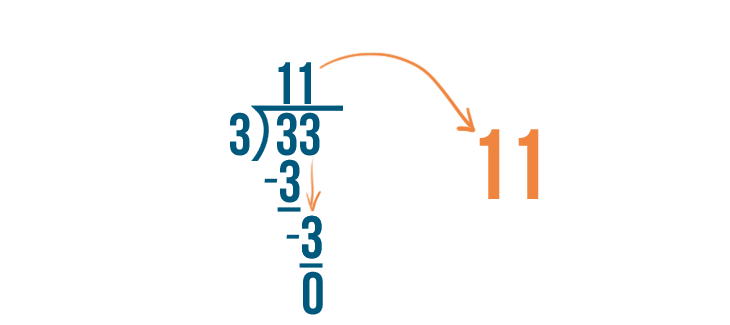
The answer, 11, will become our whole number.
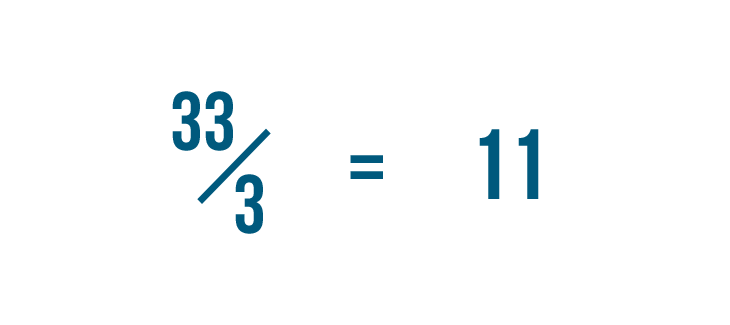
There is no remainder, so we can see that our improper fraction was actually a whole number. 33/3 equals 11.

Try This!
Try converting these improper fractions into mixed numbers.
/en/fractions/adding-and-subtracting-fractions/content/